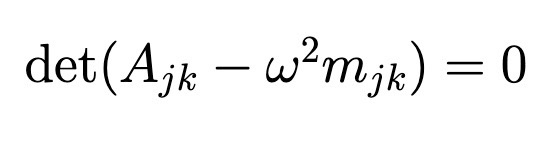Physics GRE Prep

Bohr Model, energy shell transition energy

Rydberg Formula

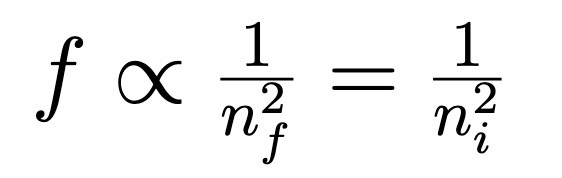
Bohr Model, angular momentum (L)

L = nh

Bohr Model, Do electrons radiate from acceleration around nucleus?

No

H Atom Pert, Relative strength of fine structure

Smaller than Bohr energies

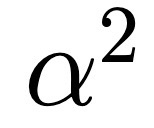
H Atom Pert, What is fine structure pertubation?

Hydrogen energy levels depend on total spin (j), m_j conserved, comes from replacing electron kinetic energy with full relativistic form and spin-orbit coupling.

H Atom Pert, Lamb Shift relative strength?

Smaller than fine structure by a factor of alpha.

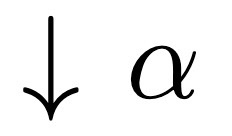
H Atom Pert, Where does Lamb Shift come from ?

Quantum electrodynamics, splits 2s and 2p energy levels with j = ½ (degenerate).

H Atom Pert, Where does Hyperfine Structure come from?

Magnetic Dipole interaction, spin-spin coupling between spins of electron and proton.

H Atom Pert, relative strength of Hyperfine Structure?

Same order of alpha as fine structure (smaller by alpha² than Bohr energies, larger by alpha than Lamb Shift). Lessened by m_e / m_p because gyromagnetic ratio depends on mass. Ground state of hydrogen split depending on singlet/triplet state (triplet higher energy).

H Atom Pert, Which correction responsible for 21cm line.

Hyperfine Structure.

Eigenvalues of Spin-Orbit Operator.

When there are definite values of j, l, and s.

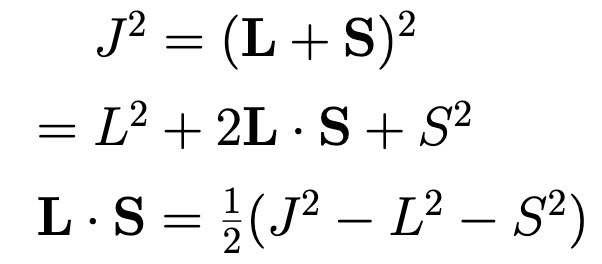
Shell Model Notation?

n - energy shells, l - orbitals

s , l = 0

p, l = 1

d, l = 2

f, l = 3

Shell Model, how many possible orbitals and states?

Possible ORBITALS (in each energy shell): 2n²

Possible STATES (in each orbital): 2(2l + 1)

Shell Model, how do shells fill?

Preferring smaller values of l, up to Argon (18), where rules break down.

What atoms are chemically inert?

Nobel Gases (full energy shells, max amount of electrons).

What atoms have an “extra” electron?

Alkali Metals, tendency to shed an electron and become and ION.

What atoms have one “too few” an electron?

Halogens, want to gain one, accounts for salts (ionic bonds).

What is Stark effect?

ELECTRIC FIELD, splitting of energy levels into closely spaced multiplets.

What is Zeeman effect?

MAGNETIC FIELD, splitting of energy levels into closely spaced multiplets.

Stark effect Hamiltonian?

For small |E| and r, can be treated as perturbation.

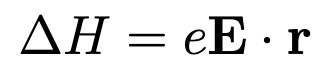
Stark effect change in ground state energy of hydrogenic atom?

None

Magnitude of splitting (Stark Effect)

Hydrogen d = a₀

First order energy shifts start happening at n = 2.

m = +- 1: unperturbed

2s and 2p with m = 0: perturbed

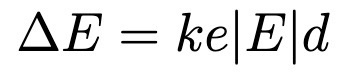
Zeeman effect Hamiltonian.

e/2m: classical gyromagnetic ratio

2 in front of S is because quantum gyro ratio is 2x classical.

Stern-Gerlach Experiment?

Zeeman effect, magnetic field splits a beam of atoms in two, measures m_j. Splitting into two sharp components showed that spin was quantized.

Zeeman Effect (small |B| and large |B|)

Small |B|: Treat Zeeman Hamiltonian as a pert on top of fine structure.

Large |B|: Treat Fine Structure as a pert on top of Zeeman Hamiltonian.

What do Selection Rules describe.

Emission and absorption of electromagnetic radiation by atoms.

Going from Psi_nlm to Psi_n’l’m’

Uses Electric Dipole approximation (wavelength of light is much larger than atom so they feel a homogenous electric/magnetic field).

Selection Rules?

• No transitions occur UNLESS delta m = +- 1 or 0

• No transitions occur UNLESS delta l = +- 1

Rules don’t allow 2s to 1s transition, but get around them because of two-photon emission. (If you shine light on Hydrogen, first excited states will populate 2p (l = 1)).

What is a Blackbody?

Absorbs ALL radiation

Reflects NO radiation

Any radiation emitted comes from its temperature

What is ultraviolet catastophe?

Black body power spectrum goes as omega³. Power would grow without bound as frequency increased.

Plank introduced second term (Bose-Einstein factor) for identical photons.

Stefan Boltzmann Law

Power goes as T⁴

T - temp

P - Power

A - Area

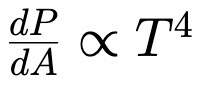
Wien’s Displacement Law

Location of Blackbody spectrum peak.

lambda max = (2.9 × 10^-3 K ; m)T^-1

Complex Conjugate

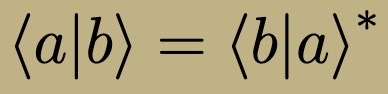
Hermitian Operator

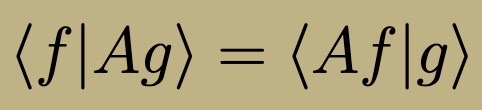
Expectation Value of an Observable

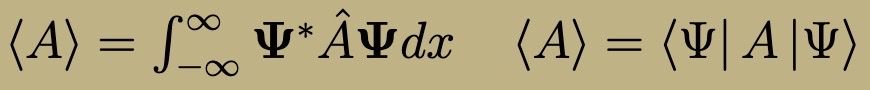
Probability of finding particle between x and x+dx

Complex Modulus

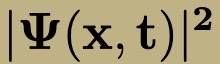
Position and Momentum Operators

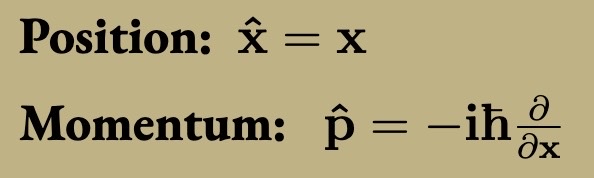
Schrodinger Equation

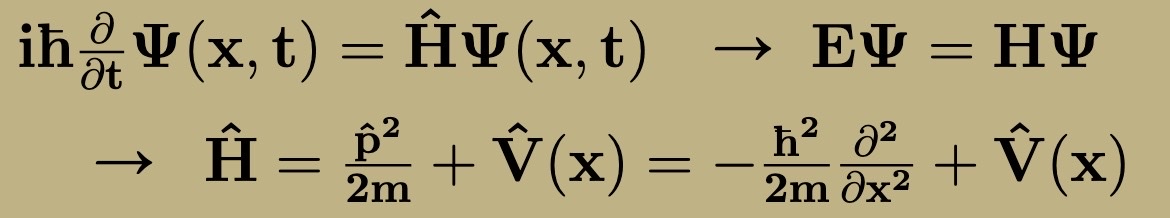
Steps for finding possible energies of system

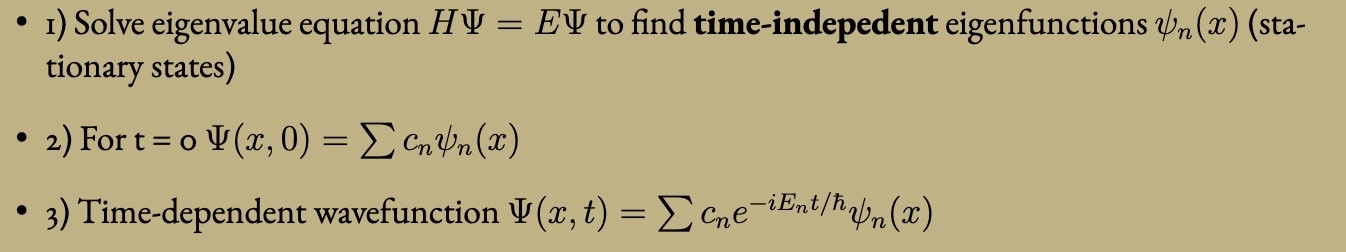
Retaining normalization, how can the wavefunction be altered.

Phase Shifted e^iθ (cancels out with Psi²).

Operator that returns same function multiplied by constant c.

f(x) is eigenfunction of operator O.

c is eigenvalue

Hermitian Operator Properties

• All eigenvalues are real

• Eigenfunctions with different eigenvalues are orthogonal (integral f(x)* g(x) = 0)

Dimension of wavefunctions.

length^-d/2 for d spatial dimensions

Expectation Value of observable A (decomp in an orthonormal basis)

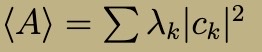
What is Hilbert Space?

Where kets live (a vector space in which inner-products may be taken)

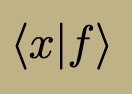
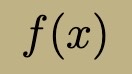
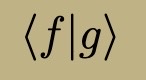
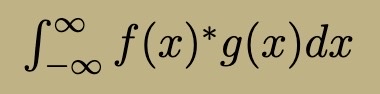
Time-Independent Energy Eigenfunction Properties

• Psi_n for different n are orthogonal (different eigenvalues)

• Psi is continuous

• Derivative of Psi (with respect to x) is continuous EXCEPT at boundary where V(x) is infinite

• Psi is purely real

• Psi_n expectation value of momentum p is 0

How many nodes for each quantum energy state

Psi₀ - 0 nodes

Psi₁ - 1 node

Psi₂ - 2 nodes

What condition of a potential V(x) must be met for definite parity

V(x) must be even

Definite Parity: Psi is either even or odd

Even psi(x) = psi(-x)

Odd psi(x) = -psi(-x)

Ground state even, first excited odd, second excited even and so on

What condition of V(x) must be true for the wavefunction to be normalizable.

E > V_min (else kinetic energy would need to be negative which is impossible)

Do Operators commute in general?

No (applying A and then B is not typically the same as applying B and then A)

Canonical Commutation Relation

[x, p] = ih

Commutators of Products of Operator Rules

[AB, C] = A[B,C] + [A,C]B

[A, BC] = [A,B]C + B[A,C]

Uncertainty Principle (Commutation Relation)

<[A,B]> means uncertainty bound depends on what state the system is in

When inequality becomes a equality, this is the minimal uncertainty bound

Uncertainty Principle

σ_xσ_p ≥ h/2

∆x∆p ~ h

∆E∆t ~ h (short decay lifetime means widely varying total energy)

An observable is conserved when?

Its operator commutes with the Hamiltonian

• We can diagnolize O and H

Hamiltonian for quantum Harmonic Oscillator

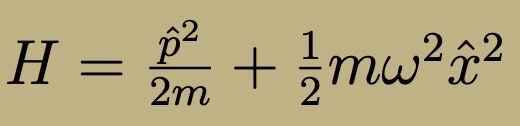
Hamiltonian Quantum Harmonic Oscillator (raising/lowering operators)

a dagger: raising operator

a: lowering operator

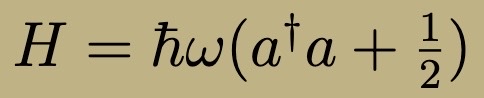
Ground state energy for harmonic oscillator

Also a minimum-uncertainty state

• position-wavefunction is gaussian

• width of gaussian is (h/m omega)^1/2

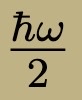
Energy spectrum of quantum harmonic oscillator-

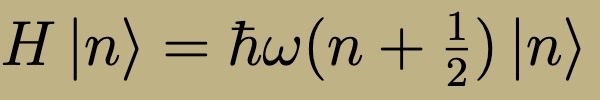
Harmonic Oscillator position-space wavefunction are related to what kind of polynomials?

Hermite Polynomials

Virial Theorem

Obeyed by all energy eigenstates of quantum harmonic oscillator

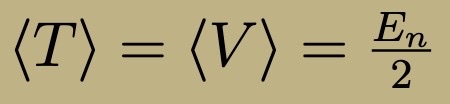
General Rules for 3D Quantum Harmonic Oscillator

Energy eigenfunctions: products

Energies: sums

Ground State: Non degenerate, First excited: three fold degeneracy

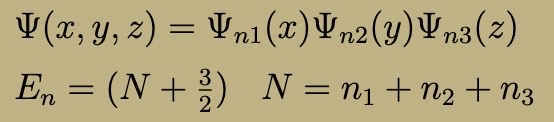
Bound Vs. Scattering States

Bound: E < 0 (LESS)

Scattering: E > 0 (GREATER)

If potential goes to infinity, every state is bound

Infinite Square Well Hamiltonian, Wavefunction, Energies

• Wavefunction continuous at boundary

• Wavefunction derivative NOT continuous at boundary

n starts at 1 NOT 0

Double mass- half the energy

Double well size - energy changes by 1/4

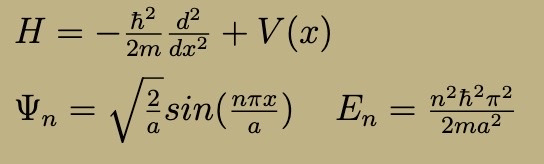
Free Particle Hamiltonian, Wavefunction, and Energies

Energy: p²/2m, de Brogile formula p = hk

• Free particle can have any momentum at all (no boundary condition to restrict k)

• Energy eigenfunctions are NOT normalizable

• Create normalizable wavefunction by forming continuous wavefunctions with different k (wave packet)

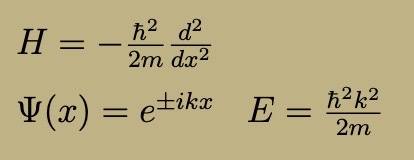
Delta Function Hamiltonian, Wavefunction, and Energy

• A has dimensions of energy x length

• Delta Function has only one bound state

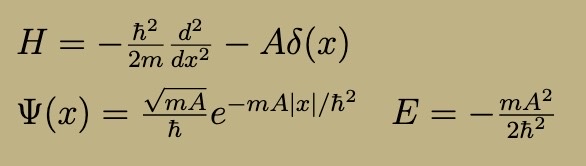
Finite Square Well

• Outside well, where V = 0, solutions are the same as the free particle (normalizable one is e^kx)

• Inside well, solutions are oscillating sins and cosines

• Potential is even, ground state is even

• As potential gets shallower and shallower, excited states disappear one by one until only one bound state remains

3D Hamiltonian

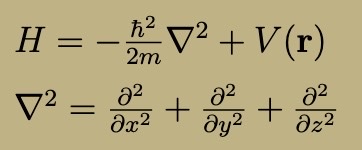
3D Commutation Relations

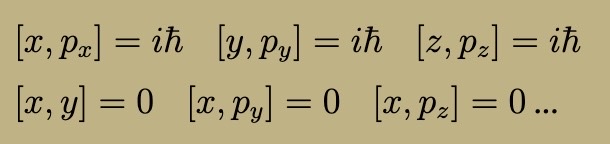
Free-Body Forces

• F_air - air resistance

• F_p - applied force

• F_kf - kinetic friction

• F_N - normal force

• F_s - spring force

• F_T - tension force

• F_sf - static friction

Kinematic Equations

• ∆x = v_i t + ½ a t²

• v_f² = v_i² + 2a∆x

• v_f = v_i + at

• ∆x = (v_i + v_f) / 2 t

2D Kinematic Equations

• x(t) = v_0x t + x₀

• y(t) = -½ gt² + v_0y t + y₀

• v_yi = v sinθ

What to use for straight up/down projectile

Conservation of energy

• mgd = ½ mv²

Circular Motion

• Centripetal Force

• a_tan = 0

• v_tan = constant

• a_rad = v²/r

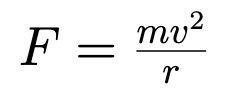
Conservative Vs Non-conservative Force

• Conservative (T + U = Constant): gravity, spring, electric

• Non-conservative: friction

Translational / Rotational Kinetic Energy

• Translational: ½ mv²

• Rotational: ½ Iω²

Gravitational / Spring Potential Energy

• Gravitational: mgh

• Spring: ½ kx²

Gravitational Force

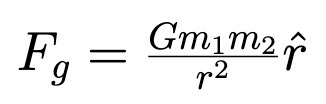
Angular Momentum (point particle and extended body)

• Point Particle: L = r x p

• Extended Body: L = Iω

Work Energy Theorem

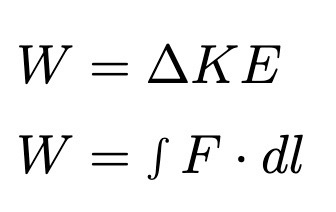
Velocity of block at bottom of curve

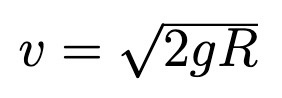
Rolling Without Slipping (velocity / energy)

• solve everything in terms of v

• friction does no work, diverts translational into rotational energy

• I goes as m

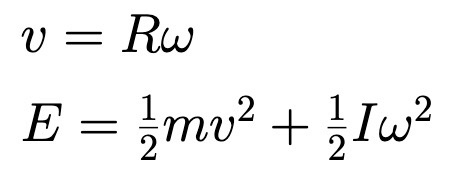
Torque

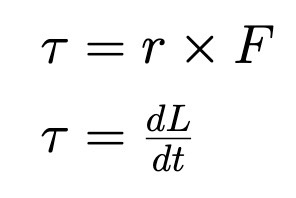
Radial Acceleration

Under Uniform Circular Motion (no tangential acc, constant tangential velocity)

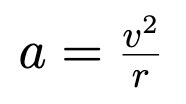
Reduced Mass

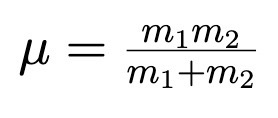
Change in Potential Energy between points a and b

When the force F is conservative.

Also means F = - nabla U

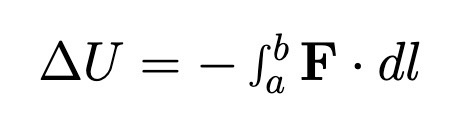
Centrifugal Force

Omega is constant angular velocity (not-inertial)

• Not a real force!

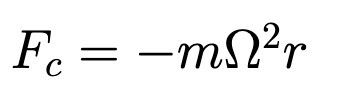
Coriolis Forc

Omega is constant angular velocity (not-inertial)

• Not a real force!

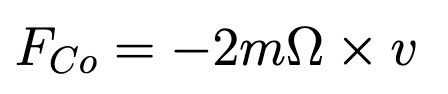
Moment of Inertia (Point Particle, Extended Object)

• Weights mass by square of distance from axis of rotation

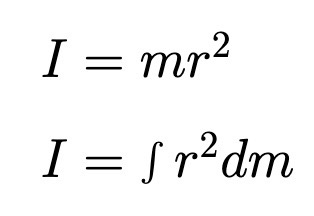
Parallel Axis Theorem

For moment of inertia of about any axis parallel to the CM axis.

• Ex. moment of inertia penny rotating around an axis that passes through the edge of the penny

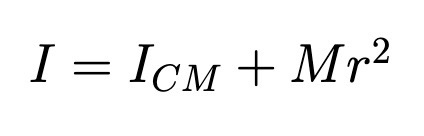
Center of Mass (Extended Object and System of Point Masses)

• Weights the mass by DISPLACEMENT from origin

• First one is really a triple integral (one for each coordinate)

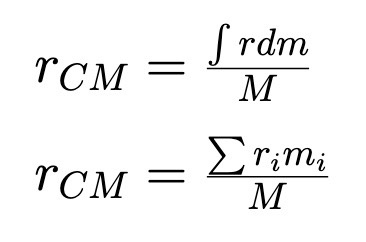
Lagrangian

Kinetic MINUS Potential

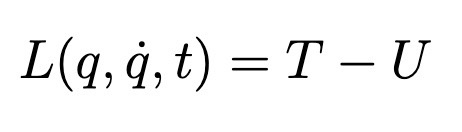
Hamiltonian (Classical)

Kinetic PLUS Potential

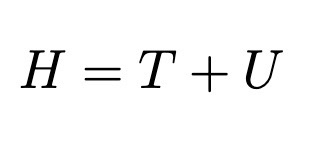
Kepler’s Laws

1. Planets move in elliptical orbits with one focus at the sun.

2. Planetary orbits sweep out equal areas in equal time.

3. T is period of planetary orbit, a is semi-major axis, k is constant same for all planets

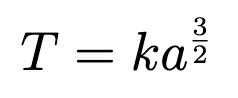
Hooke’s Law

• x is displacement of spring from equilibrium

• k is spring constant

Describes the harmonic oscillator

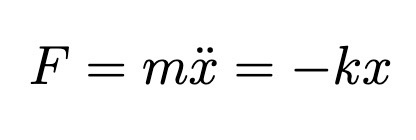
Harmonic Oscillator Solution Form (Classical)

• A is amplitude, not determined by Hooke’s law but instead by initial conditions

• Phi is the phase

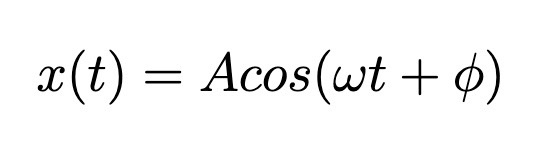
Angular Frequency of Harmonic Oscillator

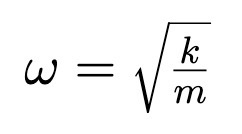
Spring Potential Energy

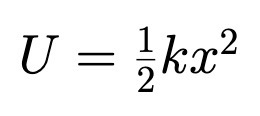
Secular Equation (Normal Modes)