Studying for Math 101

Parallel lines always/never have the same slope

Parallel lines always have the same slope

Two points on a line are (2,2) and (3,1). Find the slope of the line.

The slope of the line is -1 (m = -1)

The line y = -x + 4 will/will not enter the third quadrant

The line y = -x + 4 will not enter the third quadrant

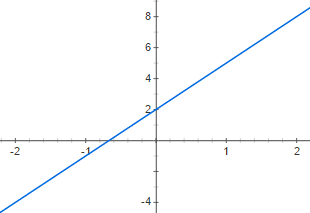
The equation for the line shown below is _____

y = 3x + 2

The line y = 3/4x + 5 will be parallel/perpendicular to the line y = -4/3x -3

These lines will be perpendicular

Find the slope and y-intercept of the following equation: 2y = 4x + 5

m = 2
y-intercept = (0,5/2)

If a line is completely vertical, that line has a(n) undefined/zero slope.

If a line is completely vertical, that line has an undefined slope

In the equation y = mx + b, m stands for _____ and b stands for _____

m = slope and b = y-intercept

If a line is completely horizontal, that line has a(n) undefined/zero slope.

If a line is completely horizontal, that line has a zero slope

Two points on a line are (2,2) and (3,1). Find the y-intercept of the line.

The y intercept is (0,4)

The three main ways to solve a system of equations are _____, _____ , and _____ .

Graphing, substitution, and elimination are the three main ways to solve a system of equations

Solve this system of equations
2x + y = 4
x + 2y = 2

(2,0)

The x and y intercepts of 4x + 2y = 8 are _____

x-intercept = (2,0) and y-intercept = (0,4)

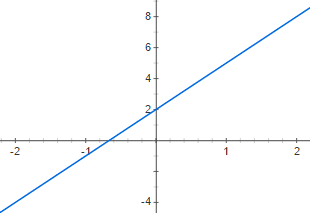
The slope of the line shown below is _____

The slope of the line is 3 (m = 3)

The process of finding a determinant with matrices larger than 2x2.

Calculate multiple smaller determinants first and combine them by alternating subtraction and addition of the determinants.

The rule for multiplying matrices.

The number of columns in the first matrix must match the number of rows in the second.

The part of an absolute value equation that tells you the graph will be translated horizontally.

When adding or subtracting within the absolute value sign:

y = |x-3| (shifts 3 right)

The method to evaluate an absolute value expression.

Evaluate as usual. Treat the Absolute Value symbols as parentheses and use PEMDAS.

x |2 + y| - z when x = 2, y = -5 and z = 3

(2) |2+ (-5)| - 3

(2) |2 - 5| -3

2 |-3| -3

2 (3) -3 {absolute value of -3 is 3}

6 - 3 = 3

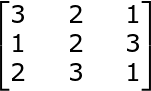
Find the determinant

3((2 * 1) - (3 * 3)) - 2((1 * 1) - (2 * 3)) + 1((1 * 3) - (2 * 2))

3(2 - 9) - 2(1 - 6) + 1(3 - 4)

3 * -7 - 2 * -5 + -1

-21 + 10 - 1

-12

Matrix

Main ingredient of Linear Algebra. Used to solve systems of equations.

The rule for adding matrices.

Number of rows and columns match exactly.

Evaluate:

2 |4 - 8|

First simplify inside absolute value sign: 4 - 8 = -4

Then take absolute value: |-4|= 4

Then multiply by number outside: 2 x 4 = 8

Solve:

|x| = -3

No solution

You cannot equate an absolute value to a negative number.

Evaluate

|-2|

2

Absolute Value Reflection

A special transformation which flips the Absolute Value graph so that its vertex is at the top of the graph.

The three things that will occur in the graph of this equation.

y = -4 |x - 3| -3

Reflected due to the absolute value being multiplied by -4.

Translated right 3 places due to the -3 in the absolute value.

Translated down 3 places due to the -3 outside the absolute value.

Add:

|3 4| + |-2 5|

3 + -2 = 1

4 + 5 = 9

thus;

|1 9|

The process of multiplying matrices.

M = matrix, R = row, C = column, A = answer

M1R1 x M2C1; Add products = 1st entry R1A

M1R1 x M2C2; Add products = 2nd entry R1A

M1R2 x M2C1; Add products = 1st entry R2A

continue

Translation (in graphing)

Operations that move the graph of an absolute value equation horizontally or vertically.

The part of an absolute value equation that tells you the graph will be a reflection.

The absolute value is multiplied by a negative: y = - |x|

Solve |4x + 1| = 11

Split the equation:

4x + 1 = -11 and 4x + 1 = 11

Solve normally

x = -3 and x = 2.5

Transformation (in absolute value graphs)

Anything that changes the way an absolute value graph looks.

The process of adding matrices.

Add each component to its corresponding component in the other matrix.

The importance of Square Matrices.

You can only calculate a Determinant on a square matrix.

The number of possible answers for absolute value equations.

Two

(|x|= 3; x = 3 or -3)

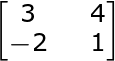
Find the determinant

Multiply the diagonals and subtract the products:

(3*1) - (-2*4)

3- (-8)

3 + 8 = 11 is the determinant

The part of an absolute value equation that tells you the graph will shift vertically.

When adding or subtracting outside the absolute value sign:

y = |x| + 3 (shifts up 3 places)

Absolute Value

The magnitude of a number (distance from 0) regardless of sign.

Determinant of a Matrix

A number found from multiplying the diagonals and subtracting the products.

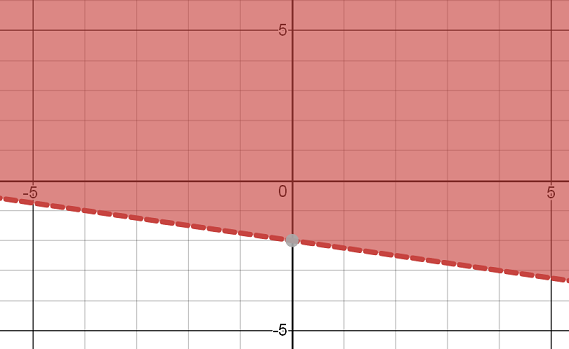
Write the inequality shown below.

The inequality is y > -x/4 - 2.

How do you graph the inequality y > x - 4?

Find the solution to 4 - 3x < 10

The solution is x > -2

Find the solution to -t/8 > 3

The solution is t < -24

Find the solution to 2n - 9 > 1

The solution is n > 5

A dashed line is used to graph any two-variable inequality that contains either of these symbols.

When a two-variable inequality contains either less than (<) or greater than (>), a dashed line will be used to graph the boundary line.

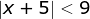
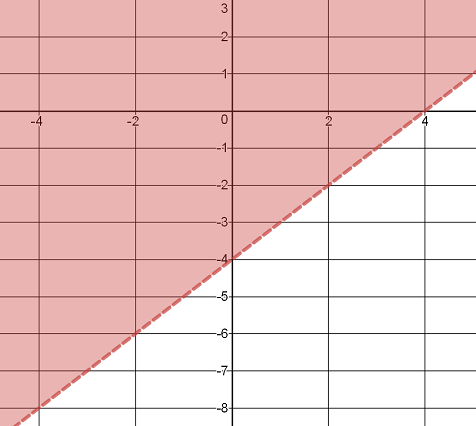
Find the solution.

The solution is all x-values such that x > -14 and x < 4.

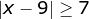
Find the solution.

The solution is:

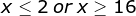
Find the solution to x + 4 < 12

The solution is x < 8

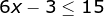
Find the solution to the following inequality.

The solution is:

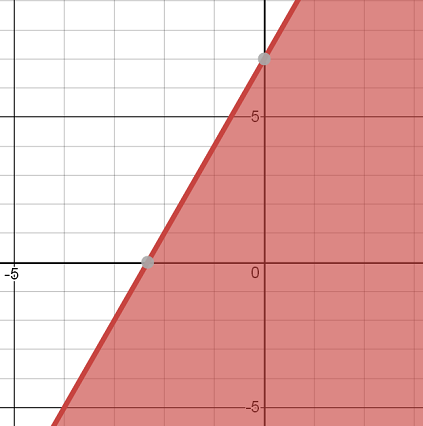
Write the inequality shown below.

The inequality in slope-intercept form is:

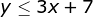
Represent the following in interval notation.

x > -3 and x < 5

The interval notation is (-3, 5).

Find the solution to -4x/5 < 4

The solution is x > -5

Solve:

(x+2)² = 8 + 4x

Expand and solve for standard form:

x² + 4x + 4 - 8 - 4x = 0

x² - 4 = 0

Solve with zero product

(x - 2)(x + 2) = 0

x = 2 or -2

Identify the parts of the graph in this vertex form equation.

y = -5(x + 1)² - 2

-5 = concave down

y-intercept = -7 (substitute x = 0)

axis of symmetry x = - 1 (from equation)

Purpose of completing the square

To change a standard form equation into a vertex form equation.

Type of equation that leads to a parabola graph.

Quadratics with squared terms such as x2.

A trinomial can be factored into a Perfect Square when...

ax² + bx + c

and

(b/2)² = c

The process of factoring non-1 leading coeffecient trinomials.

Need 2 numbers whose sum is the middle coefficient.

Product of the numbers =product of the constant and the leading coefficient.

Work backwards to get correct coefficients for each binomial.

Process to factor quadratics, using x2 + 7x + 6 as an example.

Factor constant term (6): 6*1, 2*3, -6*-1, -2*-3

Add factors to find middle term number (7x): 6 + 1 = 7

Separate factors into product of binomials

(x + 6)(x + 1)

Factors

Values that when multiplied together give an original number.

Ex: the factors of 15 are 5 and 3 (5*3=15)

Maximum of a Parabola

Highest point on the U shaped graph.

Product

Answer to a multiplication problem.

Vertex of a Parabola

The point at which a parabola changes direction.

Concave down it is the maximum.

Concave up it is the minimum.

Zero Product Property

Solving quadratics by factoring into a product of binomials equal to zero. This offers two binomials to set equal to zero in order to get solutions to the original quadratic.

Find the vertex of: y = 3x² + 6x +1

Axis of sym: x = -(6)/2(3) = -1

Sub: y = 3(-1)² + 6(-1) + 1 = -2

Vertex point (-1,-2)

Leading Coefficient

The coefficient (number being multiplied) of the first term in a polynomial.

The graph of which of these equations are parabolas:

a. y = x + 1

b. y = x⁵ - 1

c. y = x² - 6

d. y = 2x²

Quadratics with squared terms only lead to parabolas, so c. and d. are parabolas.

Process of completing the square

Change the c (using algebraic rules) so that it equals (b/2)².

Process to solve quadratics that are not in standard form.

Use algebraic rules to rewrite the equation in proper standard form, then solve with the zero product property or the quadratic formula.

Give the roots of this function:

f(x) = x² - 4x + 4

The roots are both 2.

(x - 2)(x - 2) = 0

x - 2 = 0

x = 2

Characteristics of a Parabola:

• Looks like a U shape

• Has 1 vertex

• Always symmetrical

• Shape of the path of a thrown object

Factor: x² - 4

constant factors: 2 * -2

sum of factors=0=middle term of (0x)

use factors in binomials

(x + 2)(x - 2)

Perfect Square Binomial

A binomial that is squared: (x - h)².

Find the solutions:

x² - 3x + 2 = 0

Factor into binomials:

(x - 2)(x - 1) = 0

x - 2 = 0

x - 1 = 0

x = 2 and x = 1

Use the quadratic formula to determine the discriminant of: x² - 3x +1

Discriminant of Quadratic Formula is b² - 4ac

-3² - 4(1)(1) = 5

FOIL

A binomial (expression with two terms) is multiplied by a binomial.

Multiply: First terms in each binomial, Outside terms, Inside terms, then Last terms.

Factor: 3x² - 14x - 5

+ = -14

* = (3 * -5) = -15

numbers are 1 and -15

factor -15 (3 * -5)

final: (3x + 1)(x - 5)

Axis of Symmetry

Line at which a graph could be folded and it would be the same on both sides. It goes straight down the middle.

Root of a Function

A solution when the function equals 0. The roots of a function are the numbers, which when multiplied together give the original function.

Quadratic Formula

The quadratic formula:

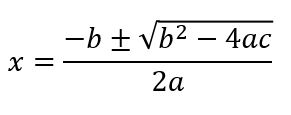
Discriminant of the Quadratic Formula

Inside the sqrt sign: b2 - 4ac

Multiply:

(x - 5)(x + 2)

F: x * x = x²

O: x*2=2x

I: -5 * x = -5x

L: -5 * 2 = -10

x² - 3x - 10

Identify the parts of the graph in this standard form equation:

y = ax² + bx + c

y = ax² + bx + c

a = concave up (pos) or down(neg)

y-intercept = c

axis of symmetry: x = -b/2a

vertex: sub x = -b/2a in to get y value for coordinate point (x,y)

Solve using complete the square:

x² + 2 = 6x - 2

1. Standard form: x² - 6x + 4 = 0

2. (b/2)² = (-6/2)² = 9

3. to make c = 9 add 5 to both sides

4. x² - 6x + 9 = 5

5. factor perfect square and solve (x - 3)(x - 3) = 5

x - 3 = 5

x = 8

The Standard Form of a Quadratic Equation

y = ax² + bx + c

Simplify a math expression

Reduce to lowest terms

Simplify: 92/3

cube root of 9 squared =

cube root of 81= 4.33

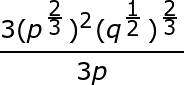
Simplify:

Use exponent rules to simplify:

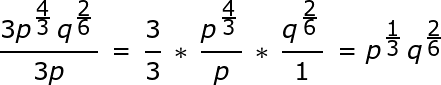
Cube root is the same as

raising to the power of 1/3

Use synthetic division:

1 | 1 0 4 (opposite of constant in the divisor divided into coefficients in order in the dividend)

bring down 1.

1 * 1 = 1, 0 + 1 = 1

1 * 1 = 1, 4 + 1 = 5

ans 1 1 5

dividend is 2nd degree; ans is 1st degree

x + 1 R5

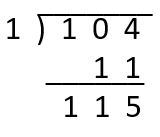
Simplify:

Break it up to simplify each part.

3/6 = 1/2

x⁵/x² = x³

y⁵/y⁷ = 1/y²

answer: x³/2y²

Exponent Properties:

Quotient of a Power

Subtract:

x⁵ / x³ = x^5-3

x²

Divide:

(x³ - 1) divided by (x² + 1)

Step 1: x² + 0x + 1 into x³ + 0x² + 0x - 1

Step 2: x³/x² = x (first ans. term)

Step 3: x(x² + 0x + 1) = x³ + 0x² + x

Step 4: sub. & bring down= -x - 1

Step 5: x² doesn't go into -x

Ans: x + (-x - 1)/(x² + 1)

Five Main Exponent Properties

Product of Powers

Power of Powers

Quotient of Powers

Power of a Product

Power of a Quotient

Matching functions to graphs of cubics, quartics, quintics and beyond

Step 1: substitute 0 for x to find y-intercept

Step 2: find values for x = 1 and -1

Step 3: plot more points (opposite matches is great 2 and -2 etc) until sketch becomes clear

Exponent Property:

Product of Powers

Add

x² * x⁴ = x²⁺⁴

x⁶

Exponent Property:

Power of a Quotient

Distribute the exponent:

(x/y)³ = x³/y³

Synthetic division

method of dividing polynomials by using only the coefficients of the terms

Subtract:

(x³ - x² + 1) - (x³ - x² + x)

step 1: x³ - x² + 1 - x³ + x² - x

step 2: 1 - x (add like terms and simplify)

Convert to Rational exponents:

fourth root of the square of 3x

(3x)^2/4