Multiple Regression

Homoscedasticity

ANOVA - equal variances within each group

regression - constant across all x values

Dependent Variable

goal of the study; outcomes in a study

Regressors

variables that are being used to predict some outcome measure; can be independent or control

Independent Variable

variables that are of interest to our research question; focus of our study

Control Variable

variables that help explain the dependent variable but aren’t of interest to the research question; a variable expected to influence the outcome measures but is not related to the primary research question

How are control and independent variables treated differently?

mathematical processes of calculating regression eqn (no difference) but interpreting the results of the study is since independents are given the most weight in the presentation of results and discussion while including control variables is not considered as contributing to Type 1 error

Why do we include control variables in the model?

may explain some of the variance making the overall prediction better; control variable may be somewhat correlated w/ both the independent and dependent variable

Goal of Multiple Regression Model

use least squares method to calcuulate bo, b1, and b2

Assumptions

same as simple regression; regressors are not strongly correlated w/ each other (can have some correlation but don’t have strong correlation)

Process

1. perform single regression between regressors (calc least squares eqn. of regressor A as a fcn of regressor B)

2. calculate regressor controlled for other regressor (calc deviation of each datum from least squares line) (repeat this and above for regressor B as a fcn of A)

3. perform simple correlation between controlled regressor and dependent variable 

4. perform simple regression between regressors

5. calculate regressor controlled for each regressor

6. perform simple correlation between controlled regressor and dependent variable

7. solve for bo using the mean value for all 3 variables (finds intercept value)

Problems with Multiple Regression when 2 Regressors are well Correlated

r² ~ 1; when trying to control either way, the values would be basically 0 if not 0

Problems with Highly Correlated Values

controlled for variables will be small (need enough spread to see a line → need more variance); difficult to know which variable is affecting your outcome

How to Treat Multiple Regressors that are well Correlated

only include 1 regressor in model at a time; may choose to select regressor that is expected to be stronger based on theory or has a better case for causality; may try regression w/ each variable separtely and pick regressor w/ better fit

R

R² represents the amount of experimental variance predicted by the model

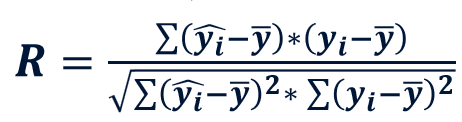
Advantages of Including Control Variables

more certainity in correlation and control more of the variance

Risk of Including Control Variables

low variance because small control values