FINALS Flashcards

continuous-variables assumption

proportionality assumption

certainty assumption

continuous-variables assumption

proportionality assumption

certainty assumption

requires that the decision variables can take on any nonnegative values (not just integer values) as long as they satisfy all the constraints.

which requires that all the functions in the decision model must be linear functions.

another key assumption is the _, which requires (as a close approximation) that all the parameters in the decision model must be known constants.

integer programming (or integer linear programming).

mixed integer programming.

Many problems arise in practice that completely fit linear programming except that the decision variables need to have integer values, thereby violating the continuous-variables assumption. The name given to such problems is __

For problems where only some of the decision variables are required to be integer, the name is _

binary variables

binary integer programming

It often is convenient to use _ (variables whose only values are 0 or 1) to represent yes-or-no decisions, where a value of 1 indicates a yes decision and a value of 0 indicates a no decision. The name given to problems with such binary variables is _. After describing the nature of integer programming in general, Chapter 10 focuses on using binary integer programming to deal with yes-or-no decisions

proportionality

The other chapter in Part 4, Chapter 11, focuses on nonlinear programming. Nonlinear programming problems completely fit linear programming except for the one major change that the _ assumption is violated. Therefore, some or all of the functions in the decision model now are nonlinear functions instead of linear functions.

t

Examples of an integer programming problem arises when dealing with product-mix problems

t or f?

not

If the values of the decision variables are not very large (such as for the TBA Airlines problem presented in Section 6.2 where the decision variables are the number of small airplanes and the number of large airplanes to purchase), then rounding up or down typically does lead to significant differences in the value of the objective function (on a percentage basis).

In this case, rounding is (not/_) reasonable and integer constraints are needed.

Binary decision variables

_ are variables that can have only two values, 0 and 1. They are widely used in integer programming models to represent yes-or-no decisions, where a value of 1 corresponds to a yes decision and a value of 0 corresponds to a no decision. Such models are called binary integer programming (BIP) models.

binary variables

Because the decision for each of the five proposed research and development projects is a yes-or-no decision, the corresponding decision variables are _.

mutually exclusive alternatives

These two alternatives (build a warehouse near Los Angeles or build a warehouse near San Francisco) are referred to as _ because choosing one of these alternatives excludes choosing the other

contingent

the warehouse decision is referred to as a _ decision, because the decision depends on a prior decision regarding whether to build a factory there. In general, one yes-or-no decision is said to be _ on another yes-or-no decision if it is allowed to be yes only if the other is yes.

not

because the concept of a shadow price and allowable range no longer applies. In contrast to linear programming, the objective function values for an integer programming problem do not change in a predictable manner when the right-hand side of a constraint is changed.

Solver’s sensitivity report is (not/_)available for integer programming problems

site selection problem

Recall that the company’s management needed to select a site (near Los Angeles or near San Francisco) for its new factory as well as for its possible new warehouse. For either of the possible sites for the new factory (or the warehouse), there is a yes-or-no decision for whether that site should be selected, so it becomes natural to represent each such decision by a binary decision variable

is this a project selection or site selection problem?

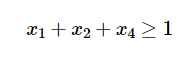
this constraint is called a _ because it covers the requirement of having a fire station located in at least one member of the set of tracts

set covering constraint

set covering problem

This type of BIP model (minimizing total cost where all the functional constraints are set covering constraints) is called a

crew scheduling problem.

With many crews and numerous trips to be covered, what is the most efficient way of assigning all the crews to all the trips? This is referred to as the _ problem

set covering constraints

(a sum of certain binary variables ≥ 1), so these too are _

Business analytics

_ (often called data science or just analytics instead) has developed a powerful methodology for performing descriptive analytics and predictive analytics.

Management science

often called operations research instead

linear programming

means the planning of activities represented by a linear mathematical model

Output cells

_ show quantities that are calculated from the changing cells.

absolute reference

relative reference

In contrast, the reference to the UnitsProduced in E7 is called an _. These references do not change when they are filled into other cells but instead always refer to the same absolute cell locations

In the formula in cell E7, the reference to cells C7:D7 is based upon the relative position to the cell containing the formula. In this case, the relative position is the two cells in the same row and immediately to the left. This is known as a .

constraint

Each _ describes a restriction on the feasible values for the levels of the activities, where a _ commonly is displayed by having an output cell on the left, a mathematical sign (≤ , ≥ , or =) in the middle, and a data cell on the right.

decision

objective

objective value

nonnegativity constraints

functional

constants

solution

feasible solution

optimal

D and W (or C12 and D12 in Figure 5.3) are the _ variables.

300𝐷+500𝑊 [or SUMPRODUCT (UnitProfit, UnitsProduced)] is the _ function.

P (or G12) is the value of the objective function (or _ for short).

𝐷≤0 and 𝑊≤0 (orC12≥0 and D12≥0) are called the _ (or nonnegativity conditions).

The other constraints are referred to as _ constraints (or structural constraints).

The parameters of the model are the _ in the algebraic model (the numbers in the data cells).

Any choice of values for the decision variables (regardless of how desirable or undesirable the choice) is called a _ for the model.

A _ is one that satisfies all the constraints, whereas an infeasible solution violates at least one constraint.

The best feasible solution, the one that maximizes P (or G12), is called the _ solution. (It is possible to have a tie for the best feasible solution, in which case all the tied solutions are called optimal solutions.)

What are the decisions to be made?

What are the constraints on these decisions?

What is the overall measure of performance for these decisions?

3 questions that need to be answered to begin the process of using the spreadsheet to formulate a linear programming model

SUMPRODUCT

There is a function in Excel called _ that will sum up the product of each of the individual terms in two different ranges of cells when the two ranges have the same number of rows and the same number of columns.

graphical method.

Linear programming problems having only two decision variables, like the Wyndor problem, can be solved by a

It is more convenient to apply the_ to the algebraic version of the linear programming model rather than the spreadsheet version.

this method cannot be used to solve problems with more than two decision variables

feasible region

The solutions permitted by all the constraints are the feasible solutions and the portion of the two-dimensional graph where the feasible solutions lie is referred to as the _.

constraint boundary line

constraint boundary equation

equality

graphical method

The line forming the boundary of what is permitted by a constraint is sometimes referred to as a _, and its equation may be called a _. Frequently, a constraint boundary line is identified by its equation.

For any constraint with an inequality sign (whether a functional constraint or a nonnegativity constraint), the general rule for obtaining its constraint boundary equation is to substitute an _ sign for the inequality sign.

objective function line

All objective function lines for the same problem are parallel

An _ is a line whose points all have the same value of the objective function

resource-allocation problems

cost-benefit-trade-off problems

mixed problems

transportation problems

assignment problems

five key categories of linear programming problems

Resource-allocation

_ problems are linear programming problems involving the allocation of resources to activities. The identifying feature for any such problem is that each functional constraint in the linear programming model is a resource constraint, which has the form

Amount of resource used

≤

Amount of resource available

only for one of the resources.

The amount available of each resource.

The amount of each resource needed by each activity. Specifically, for each combination of resource and activity, the amount of the resource used per unit of the activity must be estimated.

The contribution per unit of each activity to the overall measure of performance.

These three kinds of data are needed for any resource-allocation problem.

cost–benefit–trade-off

Level achieved

≥

Minimum acceptable level

A _ formulation enables management to specify minimum goals for the benefits that need to be achieved by the activities.

The identifying feature is that each functional constraint is a benefit constraint, which has the form _

for one of the benefits.

The minimum acceptable level for each benefit (a managerial policy decision).

For each benefit, the contribution of each activity to that benefit (per unit of the activity).

The cost per unit of each activity.

These three kinds of data are needed for any cost–benefit–trade-off problem.

resource constraints

benefit constraints

the identifying feature of a pure resource-allocation problem is that all its functional constraints are _. The identifying feature of a pure cost–benefit–trade-off problem is that all its functional constraints are _. (Keep in mind that the functional constraints include all the constraints of a problem except its nonnegativity constraints.)

resource constraint

benefit constraint

fixed-requirement constraint

types of functional constraints

Amount provided

=

Required amount

the form of a fixed-requirement constraint is

what-if analysis

This analysis is commonly referred to as _ because it involves addressing some questions about what would happen to the optimal solution if different assumptions were made about future conditions. Spreadsheets play a central role in addressing these what-if questions

sensitive parameters

What-if analysis reveals how close each of these estimates needs to be to avoid obtaining an erroneous optimal solution, and therefore pinpoints the _______ (those parameters where extra care is needed to refine their estimates because even small changes in their values can change the optimal solution).

sensitivity analysis

These sections focus on studying how changes in the parameters of a linear programming model affect the optimal solution. This type of what-if analysis commonly is referred to as _,

Parameter Analysis Report

Using a _ Generated by Analytic Solver to Do Sensitivity Analysis Systematically

parameter cell

parameter analysis report

The data cell containing a parameter that will be systematically varied (UnitProfitPerDoor, or C4, in this case) is referred to as a _. A _ is used to show the results in the changing cells and/or the objective cell for various trial values in the parameter cell.

optimal

managerial policy

The Final Value column indicates the _ solution. The next column gives the reduced costs, which can provide some useful information when any of the changing cells equal zero in the optimal solution, which is not the case here. (For a zero-valued changing cell, the corresponding reduced cost can be used to determine what the effect would be of either increasing that changing cell or making a change in its coefficient in the objective function.)

the right-hand sides of the functional constraints may well represent _ decisions rather than quantities that are largely outside the control of management.

shadow price

The _ for each constraint reveals how much the total profit from these new products would increase for each additional hour of production time made available in the corresponding plant for these products.

This interpretation of the shadow price remains valid as long as the number of hours remains within its allowable range.

The Feasible Solutions Property

Cost

A transportation problem will have feasible solutions if
and only if the sum of its supplies equals the sum of its demands

The _ Assumption: The cost of distributing units from any particular source to any
particular destination is directly proportional to the number of units distributed. Therefore, this cost is just the unit cost of distribution times the number of units distributed

assignees
tasks

The Model for Assignment Problems
Any assignment problem can be described in the following general terms. Given a set of tasks to be performed and a set of assignees who are available to perform these tasks, the problem is to determine which assignee should be assigned to each task.
To fit the model for an assignment problem, the following assumptions need to be
satisfied:
1. The number of _ and the number of _ are the same.
2. Each assignee is to be assigned to exactly one task.
3. Each task is to be performed by exactly one assignee.
4. There is a cost associated with each combination of an assignee performing a
task.
5. The objective is to determine how all the assignments should be made to
minimize the total cost.
The first three assumptions are fairly restrictive. Many potential applications do not quite
fit these assumptions.

Hungarian

There are much faster algorithms available that have been designed specifically to solve assignment problems. The most famous of these is called the _ method. In practice, one of these special algorithms normally would be used to solve large assignment problems

network

A _ can be defined as a system with a number of components where there are direct connections between various pairs of components.

nonproportional

Nonlinear programming is used to model _ relationships between activity levels and the overall measure of performance, whereas linear programming assumes a proportional relationship.

decreasing

the activity is said to have _ marginal returns because the incremental profit never increases and sometimes decreases for each incremental increase in the level of the activity.

Profit

cost

_ graphs are used when the overall objective is to maximize the total profit from all the activities. However, _ graphs are needed instead when the overall objective is to minimize the total cost of all the activities