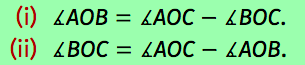Segmentos y Ángulos
5.0(1)
Card Sorting
1/37
There's no tags or description
Looks like no tags are added yet.
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
38 Terms
1
New cards
Términos indefinibles
1. Punto
2. Recta
3. Plano
4. Espacio
2
New cards
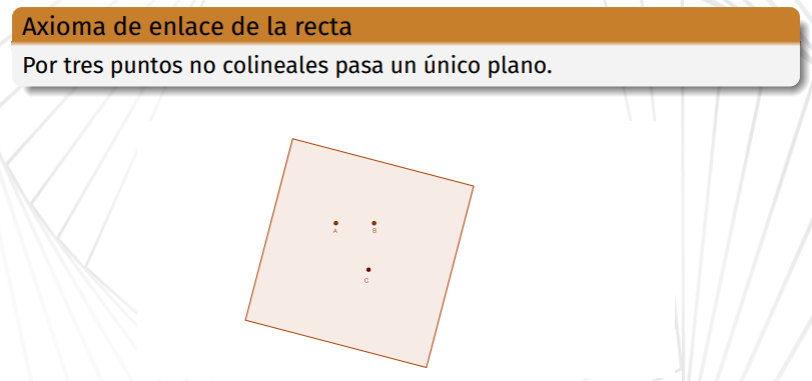
Axioma de enlace de la recta
\

3
New cards
Puntos Colineales
Tres o más puntos que están en una misma recta se llaman colineales

4
New cards
Axioma de enlace del plano
\
5
New cards
Puntos Coplanares
Cuatro o más puntos son coplanares si están en un mismo plano. Los puntos colineales siempre serán coplanares

6
New cards
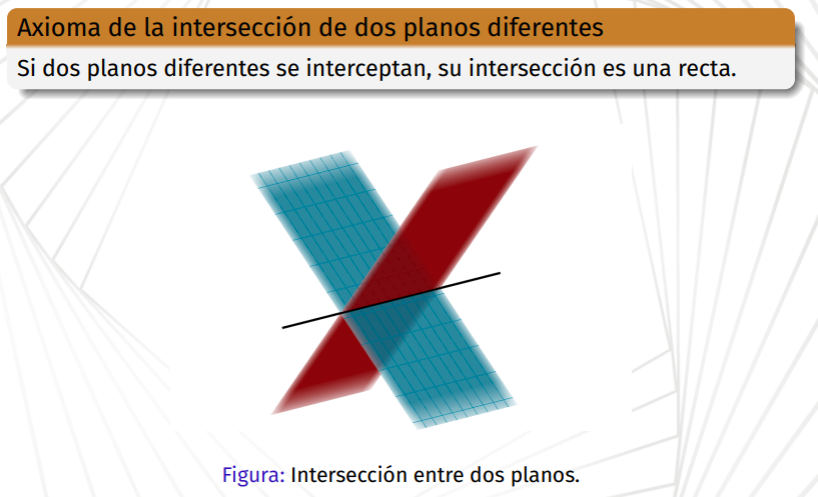
Axioma de la intersección de dos planos diferentes
Si dos planos diferentes interesectan, su intersección es una recta
7
New cards
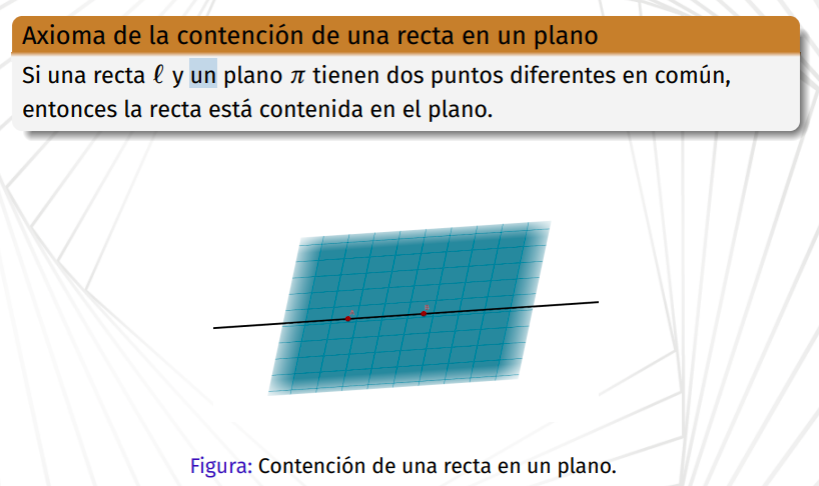
Axioma de la contención
Si una recta L y un plano π tienen dos puntos diferentes en común, entonces la recta está contenida en el plano
8
New cards
Segmento de recta
Conjunto de dos puntos formados por A y B, donde cada uno es llamdado extremo del segmento
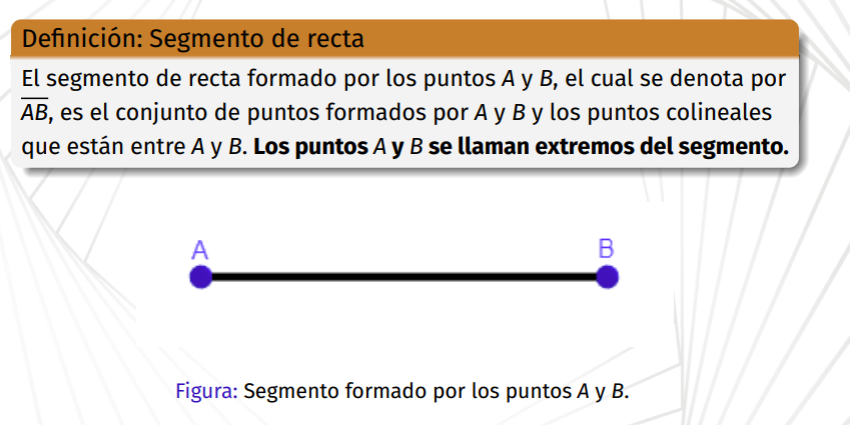
9
New cards
Medida de segmento
Es la distancia entre sus extremos. Siempre será positiva
10
New cards
Denotación de medida de segmentos
\

11
New cards
Congruencia de segmentos
Dos segmentos o más son congruentes si tienen la misma medida

12
New cards
Notación de congruencia
\

13
New cards
Propiedades de la Congruencia de Segmentos: Reflexividad

14
New cards
Propiedades de la Congruencia de Segmentos: Simetría
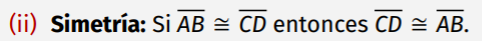
15
New cards
Propiedades de la Congruencia de Segmentos: Transitividad
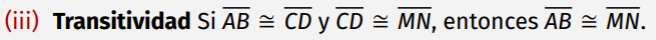
16
New cards
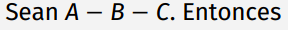
Axioma de la suma y resta de segmentos: Suma
AC = AB + BC
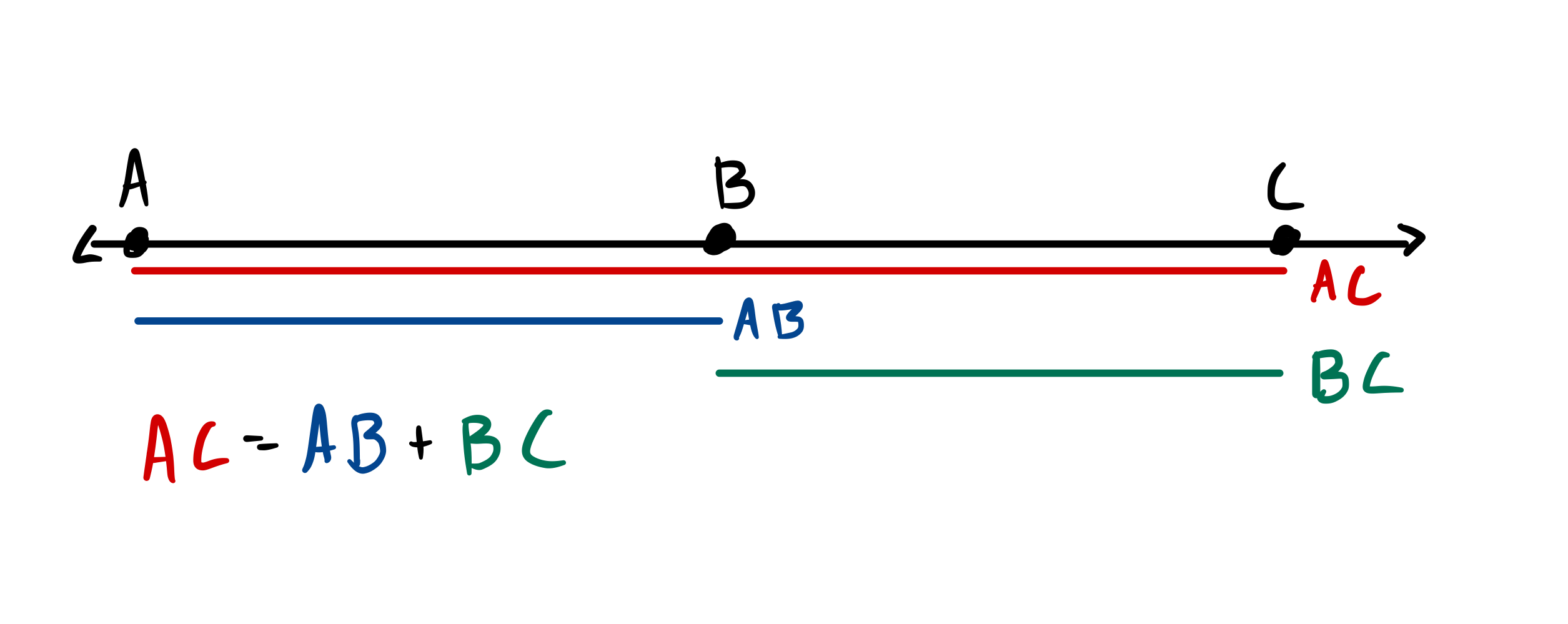
17
New cards
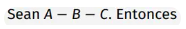
Axioma de la suma y resta de segmentos: Resta
i. AB = AC - BC
ii. BC = AC - AB
ii. BC = AC - AB
18
New cards

Punto medio de un segmento
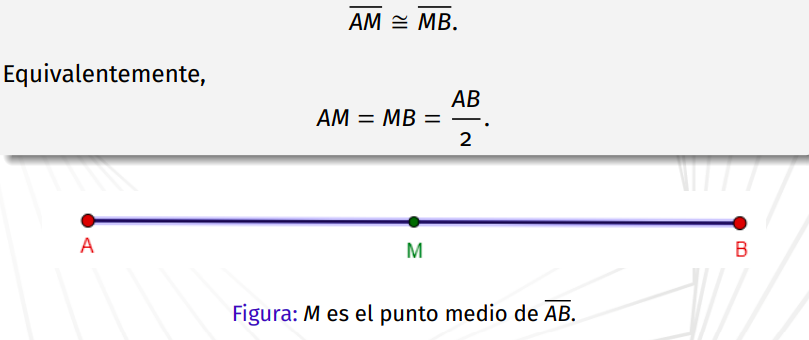
19
New cards
Teorema sobre Puntos Medios
Los puntos medios determinan segmentos congruentes
20
New cards
Definición de Semirecta
Sea O un punto de una recta L, la semirecta de origen en el punto es el conjunto de puntos x en la recta L que están de un mismo lado con respecto al punto O. Se denota
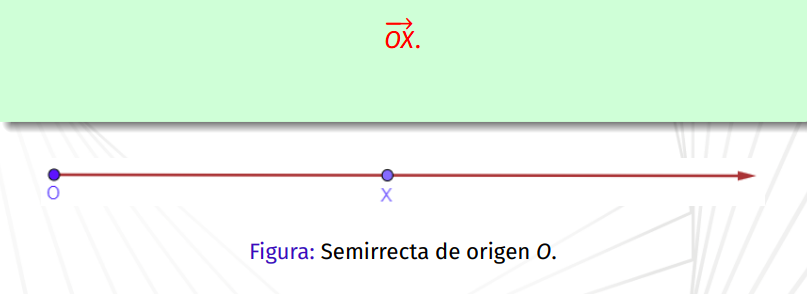
21
New cards
Definición de Ángulo
Figura geométrica formada por la unión de dos semirectas con el mismo origen
22
New cards
Notación de un Ángulo
El punto 0 es el punto de origen de la recta. El punto de origen siempre va en la mitad de la notación.

23
New cards
Definición de Medida de un Ángulo
Todo ángulo le asignamos una medida entre 0° y 180°
24
New cards
Congruencia de Ángulos
Dos o más ángulos son congruentes si tienen la misma medida
25
New cards
Notación de Congruencia de Ángulos
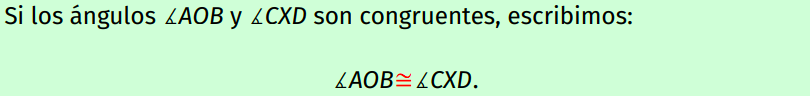
26
New cards
Clasificación de Ángulos: Ángulo Agudo
Su medida está estrictamente entre 0° y 90°.
27
New cards
Clasificación de Ángulos: Ángulo Recto
Su medida es exactamente 90°.
28
New cards
Clasificación de Ángulos: Ángulo Obtuso
Su medida está estrictamente entre 90° y 180°.
29
New cards
Clasificación de Ángulos: Ángulo Llano
Su medida es exactamente 180°.
30
New cards
Clases de Ángulos: Ángulos Adyacentes
* Tienen el mismo vértice,
* Tienen un lado en común
* Los otros dos lados están en semiplanos opuestos con respecto al lado en común.
* Tienen un lado en común
* Los otros dos lados están en semiplanos opuestos con respecto al lado en común.
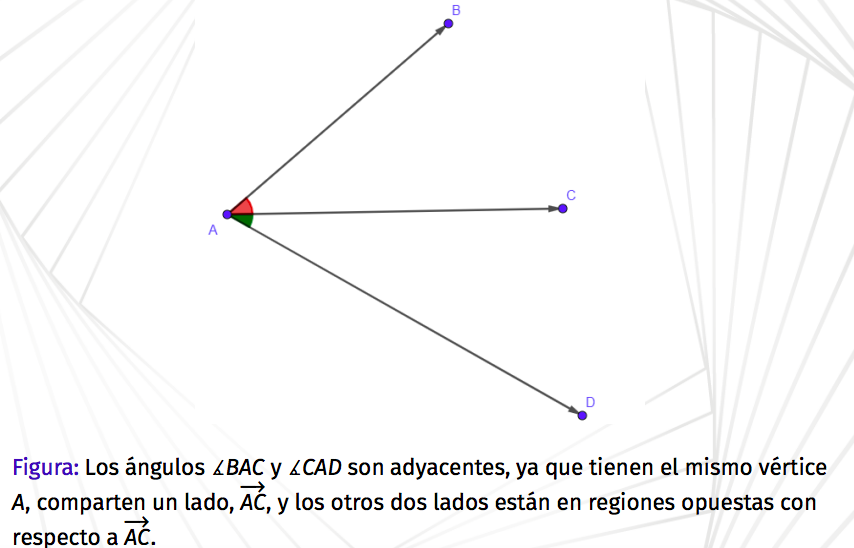
31
New cards
Clases de Ángulos: Ángulos Suplementarios
La suma de sus medidas es 180°.
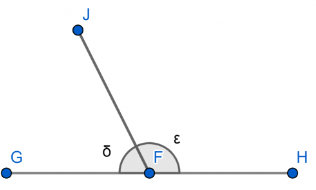
32
New cards
Clases de Ángulos: Ángulos Complementarios
La suma de sus medidas es 90°.
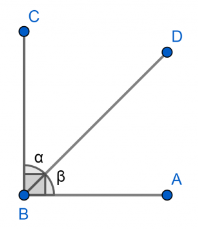
33
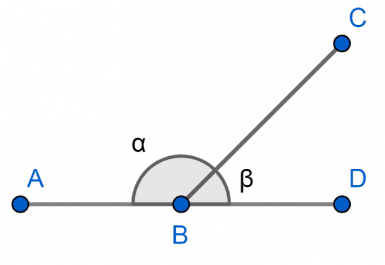
New cards
Clases de Ángulos: Par lineal
Dos ángulos adyacentes forman un par lineal si son suplementarios.
34
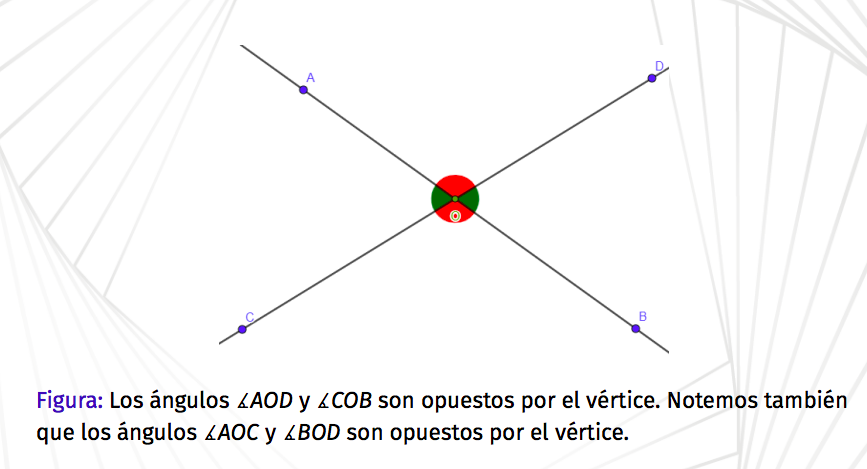
New cards
Clases de Ángulos: Ángulos Opuestos por el vértice
Tienen el mismo vértice y sus lados forman semirrectas opuestas.
35
New cards
Teorema de los ángulos opuestos por el vértice
Los ángulos opuestos por el vértice son congruentes.
36
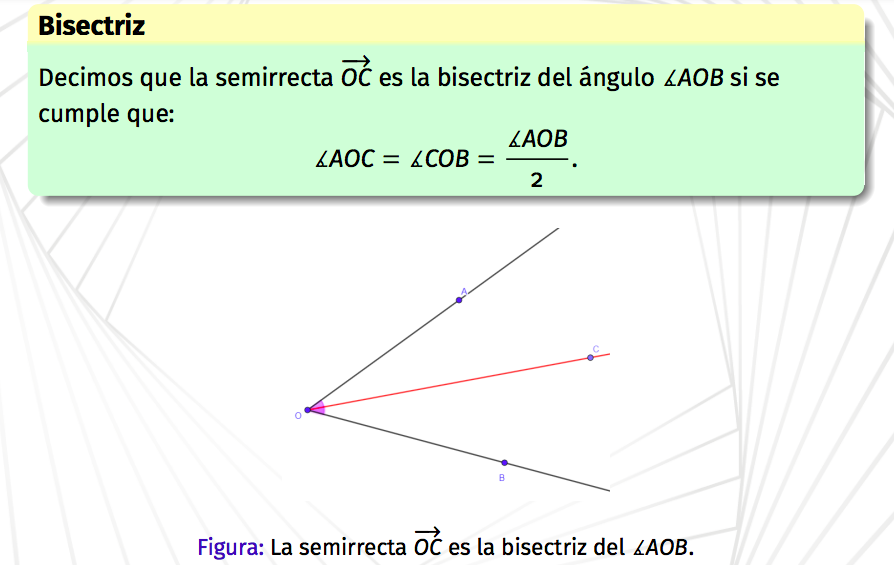
New cards
Bisectriz de un ángulo
\
37
New cards
Axioma de la suma y resta de ángulos:
Suma: Si ∡AOB y ∡BOC son dos ángulos adyacentes, entonces
Suma: Si ∡AOB y ∡BOC son dos ángulos adyacentes, entonces
\

38
New cards
Axioma de la suma y resta de ángulos:
Resta: Si ∡AOB y ∡BOC son dos ángulos adyacentes, entonces
Resta: Si ∡AOB y ∡BOC son dos ángulos adyacentes, entonces