Sets and Set Operations

Set

A set is a collection of object called elements or members of the set

An element

A member of a set.
Ex: the number 2 is an element of the set {1 2 3 4 5 6 7 8 9}

a ∈ A

If a is an element of set A, then a ∈ A denotes "a is an element of A"
Ex: A = {table, chair, bookshelf}
a = {bookshelf}
=> a ∈ A

How to determine a set?

1) A set can be described by listing all of its elements
Ex: C = {1 2 3 4 5 }
2) A set can also be described by writing a description of its elements between curly bracket
Ex: D = {x ∈ Z| 0 < x < 6}

Empty Sets

the set that has no elements at all.
Ex: P = {x∈Z| 2x + 1 = 0}
P = {Ø}

Proper subset

If and only if every element of A is also an element of B
Ex: A = {6,7,8}
B = {5,6,7,8,9}
A ⊂ B = {6,7,8}

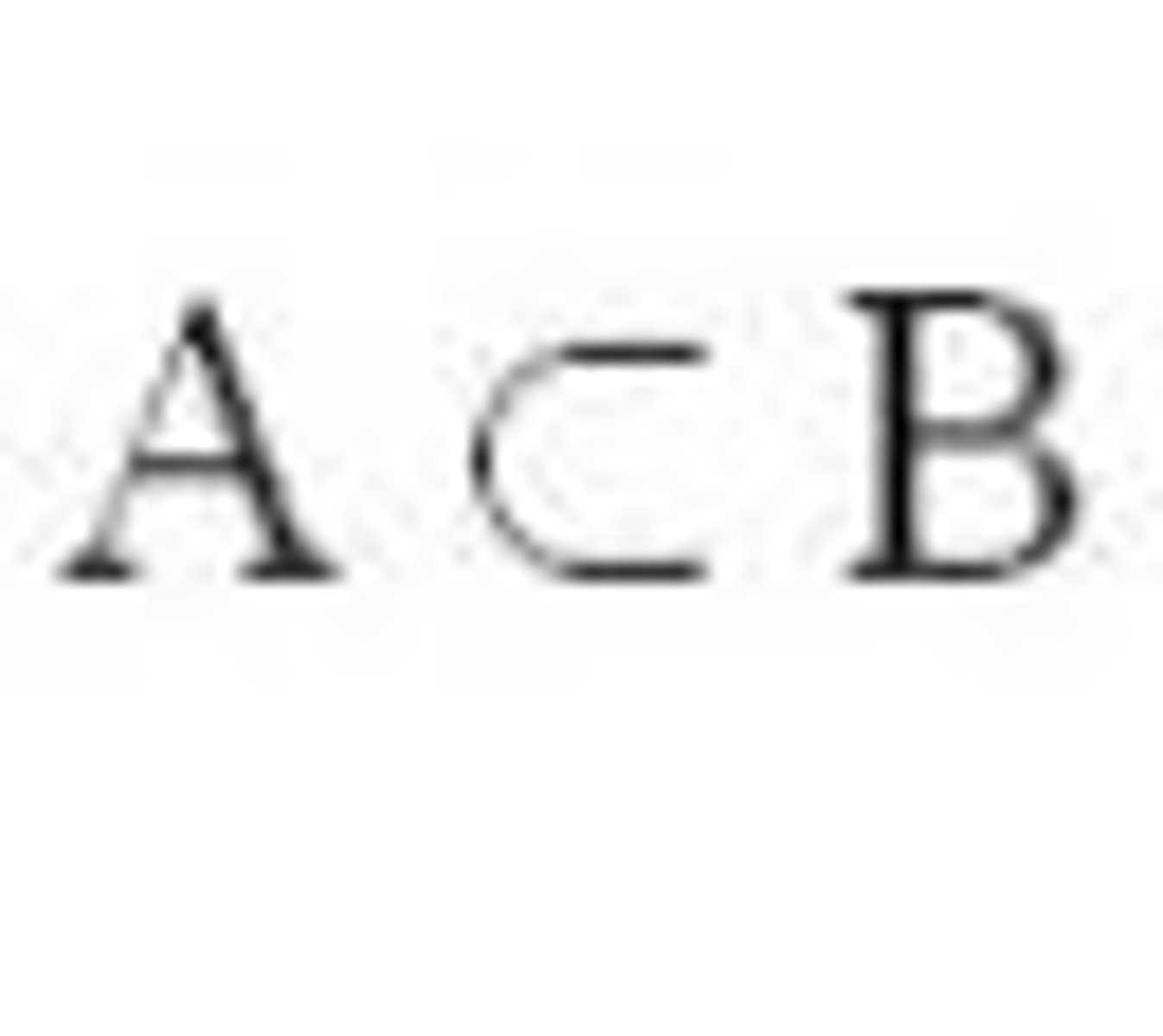
not superset

Set A isn't the superset of set B
Ex: A = {9, 14, 28}
B = {9, 66}
A ⊄ B

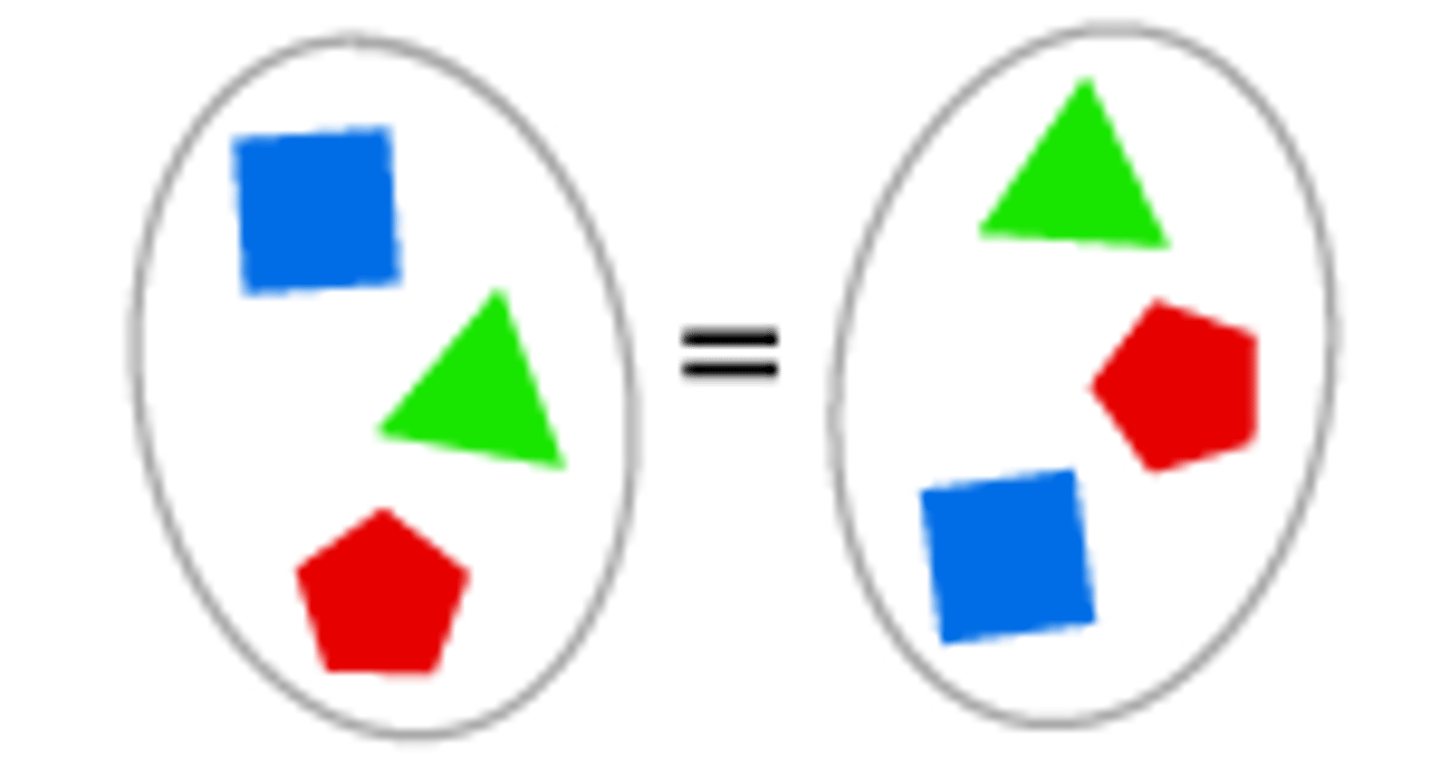
equality of two sets

Two sets have exactly the same elements
Ex: {1,2,3} = {3,1,2}

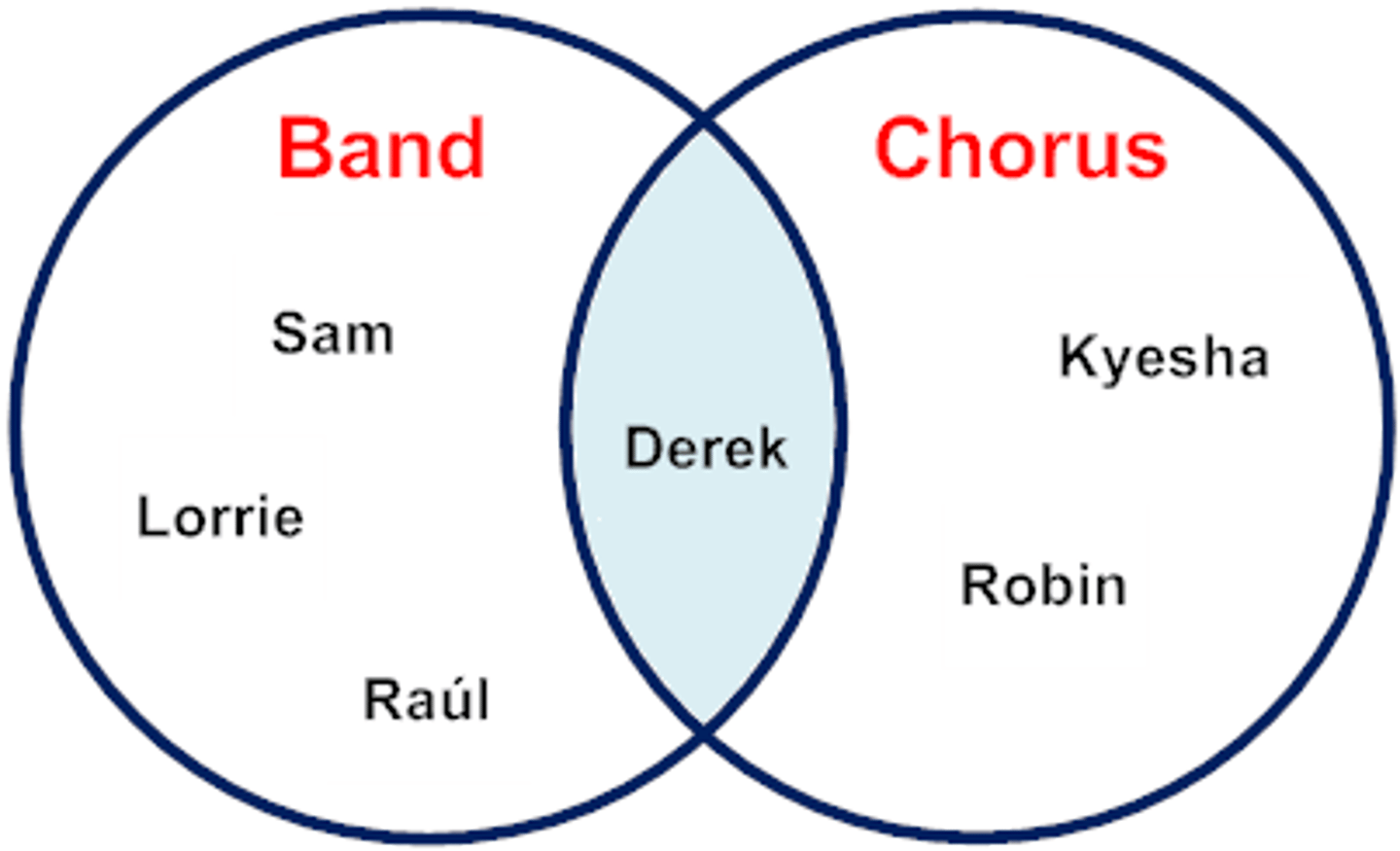
Intersection of sets

The intersection of two sets A and B consists of all elements belonging to A and to B.
The set of all elements belonging to A and to B
Ex: Band = {Sam, Lorrie, Raul, Deresk}
Chorus = {Deresk, Kyesha, Robin}
Band ∩ Chorus = {Deresk}

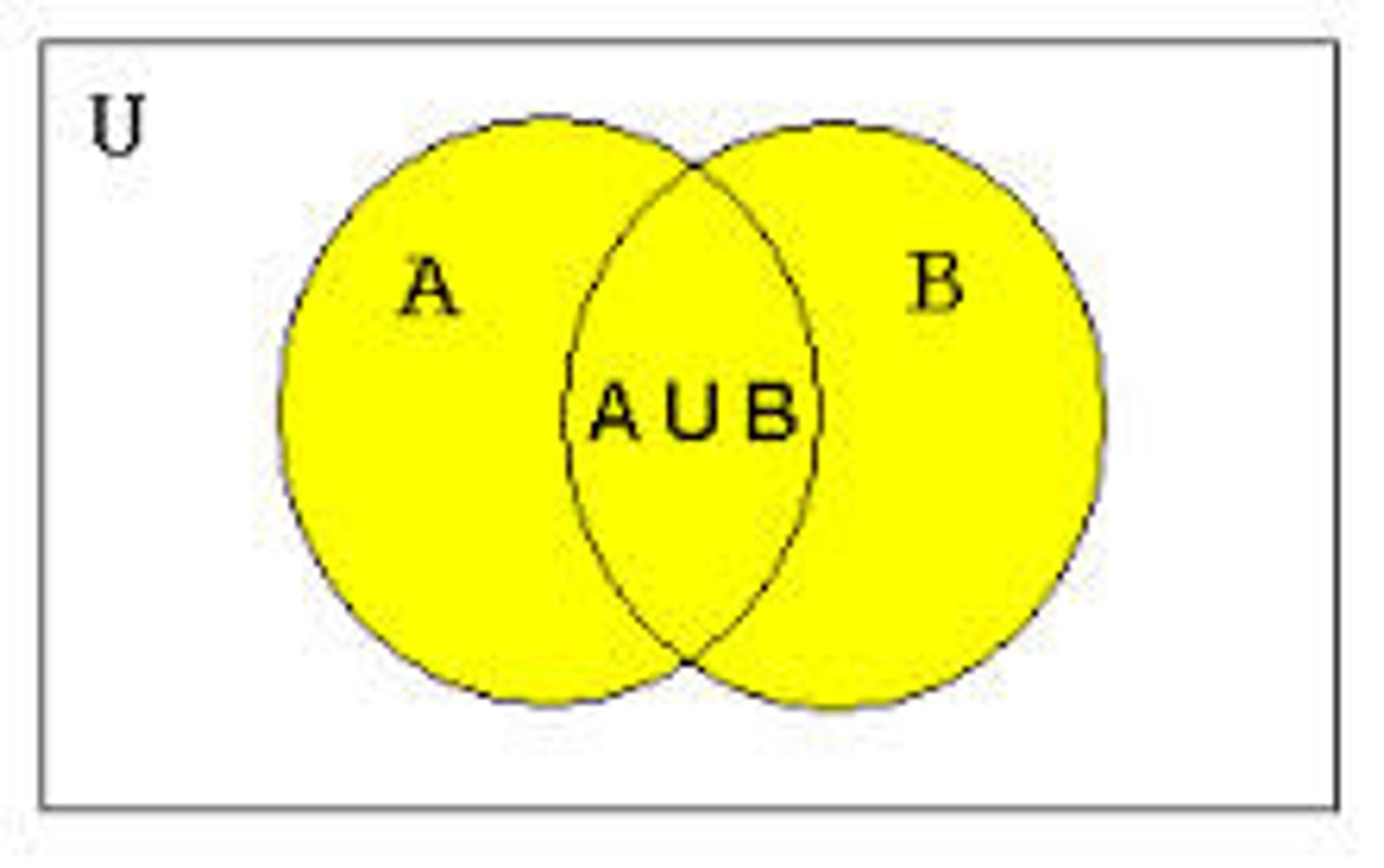
Set Operations

The set that contains those elements that are either in
A or in B, or in both.
Example: A = {2,4,6,8}
B = {3,4,7,9}
A∪B = {2,3,4,6,7,8,9}

Relative complement

The set of all element in the universal set A, but not in B'.
A = { ruler, pen, eraser, book, pencil, notebook}
B = {book, pen, ruler}
A\B = {eraser, pencil}

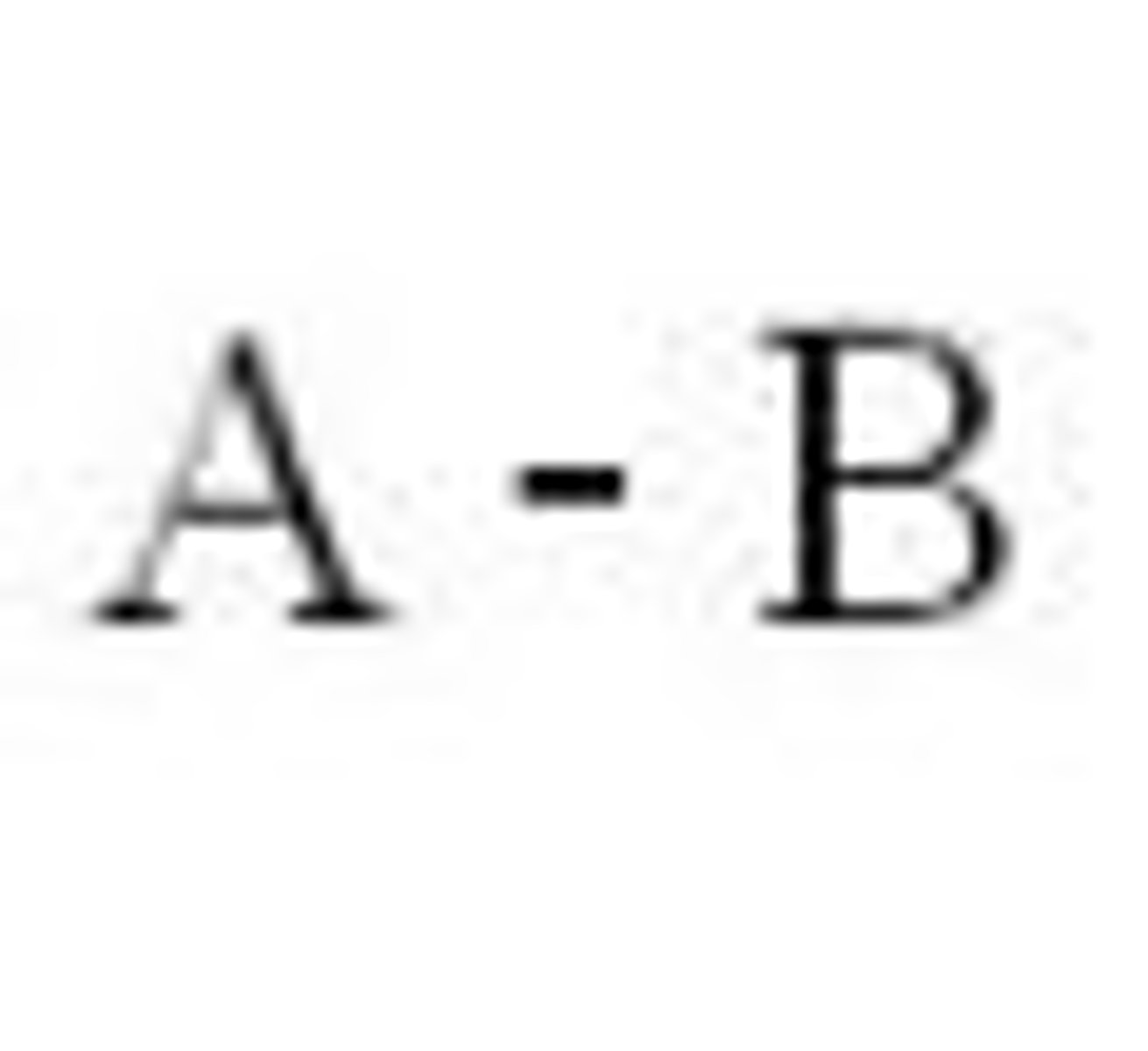
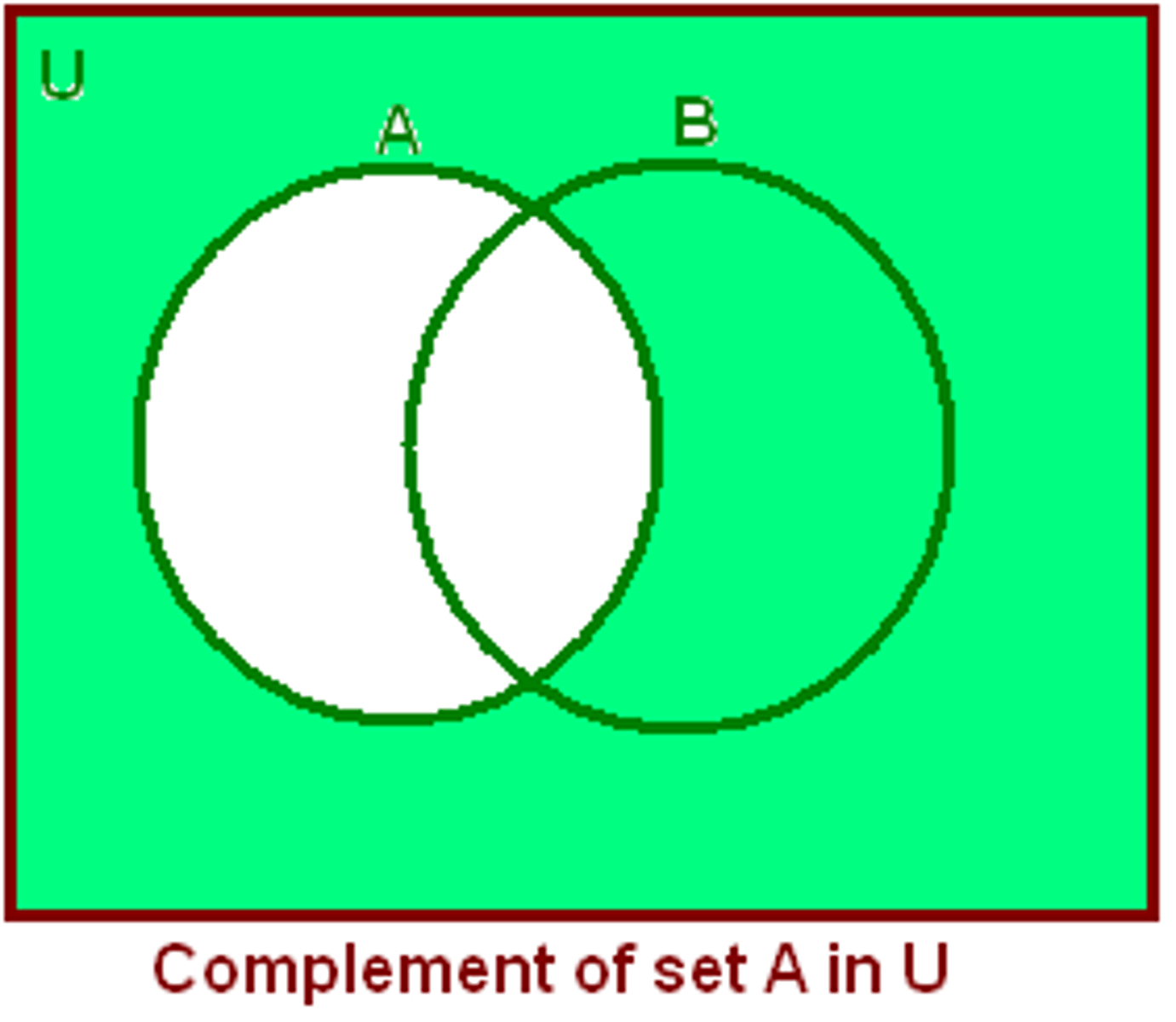
Complement of a set

The set of all elements in the universal set that are not in a given set.
Ex: Let A = {1 orange, 1 pineapple, 1 banana, 1 apple}
Let B = {1 orange, 1 apricot, 1 pineapple, 1 banana, 1 mango, 1 apple, 1 kiwifruit }
We show all elements in B, but not in A
Ac = {1 apricot, 1 mango, 1 kiwifruit}