Math Reviewer 10 - 1st QTR

Topics to cover: A. Arithmetic sequence B. Arithmetic means C. Arithmetic series D. Geometric sequence E. Geometric means F. Geometric series (finite/infinite)

Numbers or digits that multiply or divide by the same value each time.

Geometric Sequence (GS)

The difference between any two consecutive terms is always the same. 

Arithmetic Sequence (AS)

The number you keep multiplying (or dividing) by to get the next term in a geometric sequence.

Common Ratio ( r )

The pattern of the sequence in terms of n.

Explicit Formula of a Sequence

What formula is given below:

Arithmetic Series

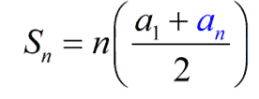
How to get the common ratio?

r = a2 / a1

How to find the common difference?

d = a2 - a1

What formula is stated below:

Geometric Means

In an infinite geometric series, if the result diverges, is it less than or more than 1?

> 1 (greater than 1)

What does n refer to?

Number of terms

What formula is formulated below:

Finite Geometric Series

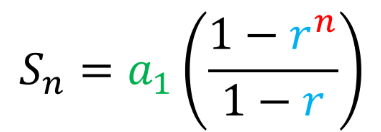
Is r = -1 / 2, divergent?

False, it converges since its absolute value of the common ratio ( | r | ) is 0.5

General formula of an arithmetic sequence.

an​ = a1​ + (n - 1) d

What formula is stated below?

Arithmetic Means

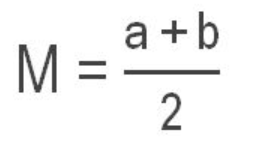
SOLVING PROBLEMS: Insert 2 arithmetic means between -2 and 25.

7 and 16

SOLVING PROBLEMS: Sn = 242, a1 = 2, r = 3, n = ? (Find n in a finite geometric series)

5 = n

SOLVING PROBLEMS: a1 = -25, a30 = -315, S30 = ? (Find the sum of the first 30 terms in an arithmetic series)

S30 = -5100

SOLVING PROBLEMS: 1.5, -3, 6, -12, . . . (which term is -3072?) (find n in a geometric sequence)

n = 11

WORD PROBLEMS: The first term of a geometric sequence is -1. Its common ratio is 2. Which term of the sequence is 4096?

n = 13

WORD PROBLEMS: Alex starts saving money by putting ₱50 in a jar on the first day.
Each day after, he adds ₱20 more than the previous day. How much money will Alex put into the jar on the 15th day? (Using arithmetic sequence)

On the 15th day, Alex will put ₱330 in the jar.

WORD PROBLEMS: A scientist places 2 bacteria in a petri dish.
Every hour, the number of bacteria triples. How many bacteria will there be after 8 hours? (Using geometric sequence)

After 8 hours, there will be 4,374 bacteria.

WORD PROBLEMS: A ball is dropped from a height of 10 meters.
Each time it bounces, it rises to 3/4 of its previous height. What is the total distance traveled by the ball (down and up) after it has bounced infinitely many times? (Using geometric series)

The ball will travel a total of 70 meters.

WORD PROBLEMS: A theater has 20 seats in the first row.
Each row after that has 4 more seats than the row before it.
If the theater has 15 rows, how many seats are there in total? (Using arithmetic series)

The theater has a total of 720 seats.

WORD PROBLEMS: A farmer plants 5 mango trees in the first year.
Every year after, he plants twice as many trees as the year before. How many mango trees will the farmer plant in the 10th year? (Using geometric sequence)

In the 10th year, the farmer will plant 2,560 mango trees.

WORD PROBLEMS: Lila runs 3 km on the first day of her training.
She increases her distance by 0.5 km each day. How far will Lila run on the 12th day? (Using arithmetic sequence)

On the 12th day, Lila will run 8.5 km.