Regression Foundations

What is regression analysis?

• A statistical tool to study the relationship between a dependent variable (y) and one or more independent variables (x)

• Goal: estimate how changes in x affect y

Difference Correlation vs Causation

Correlation: x and y move together. without implying one produces the other

• Example: Ice-cream sales and drownings rise together. The hidden driver is hot weather (a confounder), not ice-cream causing drownings

Causation: A change in X produces a change in Y, holding other factors constant (requires evidence of mechanism and identification)

• Example: In a randomized trial, giving a vaccine to one group reduces infection rates compared with a control group—random assignment isolates the causal effect

What is the basic form of the regression model?

y=β₀​+β₁​x+u

• y: dependent variable (outcome, explained, regressand)

• x: independent variable (explanatory, predictor, regressor)

• β0: intercept (expected y when x=0)

• β1: slope (effect of x on y, holding other factors constant)

• u: error term (all other unobserved influences on y)

Why do we need the error term?

• Captures all unobserved factors affecting y

• Recognizes that models cannot explain y perfectly

• Example: Wage = β₀ + β₁Education + u → u includes ability, effort, luck

What are the SLR assumptions?

Assumption	Meaning	Purpose
SLR.1	Linearity in parameters	Ensures model can be estimated with OLS
SLR.2	Random sampling	Guarantees representative sample
SLR.3	Sample variation in x	Prevents division by 0 in β̂1 formula
SLR.4	Zero conditional mean (E[u	x]=0)
SLR.5	Homoskedasticity (Var(u	x)=σ²)

Which assumptions ensure unbiasedness of OLS?

• SLR.1–SLR.4.

• Homoskedasticity (SLR.5) not needed for unbiasedness, only for efficiency

What does the zero conditional mean assumption imply?

• E[u|x] = 0 → the error term is uncorrelated with the regressor

• Without it, omitted variable bias occurs

• Example: if ability (in u) is correlated with education (x), β̂1 is biased

What is the idea of OLS?

Find β̂₀ and β̂1 that minimize the sum of squared residuals:

• SSR=∑(yi−y^i)

  Ensures best linear prediction of y given x.

What is the formula for OLS slope in SLR?

β^​1​=Var(x)/Cov(x,y)

• Intuition: slope is the standardized covariance between x and y.

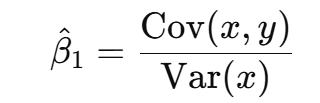
What are the key properties of OLS residuals (with intercept)?

• Sum of residuals = 0

• Residuals uncorrelated with regressors.

• Regression line passes through point (x̄, ȳ)

What does unbiasedness mean for OLS?

• On average across repeated samples, β̂ = β

• Requires assumptions SLR.1–SLR.4.

What is efficiency under Gauss–Markov?

• OLS has minimum variance among all linear unbiased estimators (BLUE).

• Requires assumptions SLR.1–SLR.5.

Does OLS require normally distributed errors?

• No, only for exact small-sample inference

• By CLT, large-sample inference works without normality

What is R²?

• Proportion of variation in y explained by the model

• High R² ≠ causality or unbiasedness

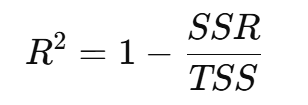
What is Adjusted R²?

• Penalizes for adding irrelevant regressors

• Can decrease when non-informative regressors are added

Can a regression with low R² still be useful?

• Yes, if coefficients are unbiased and significant

• Low R² common in cross-sectional data

What is the multivariate regression model?

• Each βj: ceteris paribus effect of xj on y.

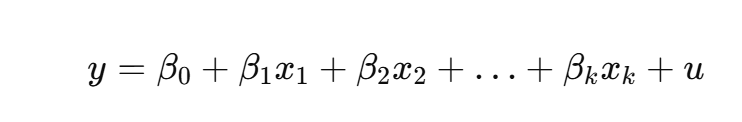
Why add multiple regressors?

• To control for confounders

• Reduce omitted variable bias

• Improve interpretation of coefficients

When does OVB occur?

• Omitted variable affects y

• Omitted variable is correlated with included regressors

Direction of bias?

Correlation(x, omitted)	Effect of omitted on y	Bias direction
Positive	Positive	Upward
Positive	Negative	Downward
Negative	Positive	Downward
Negative	Negative	Upward

Example of OVB?

• Wage regression with education but not ability

• Ability increases wages and correlates with education

• Bias: upward estimate of returns to education

Effect of rescaling x by 100?

• β shrinks by factor 100

• Predictions unchanged

• t-stats unchanged

Effect of rescaling y by 100?

• β and SE scale by 100

• t-stats unchanged

• R² unchanged

What does centering variables do?

• Subtracting mean from x

• Makes intercept represent mean outcome

• Doesn’t change slope or fit

Why use quadratic terms (x²)?

• To capture non-linear effects of x on y

• Allows slope to change with x

• Example: Wage vs. experience → concave shape.

Why include interaction terms?

• To allow effect of one regressor to depend on another

• Example: Wage = β0 + β1educ + β2female + β3(educ×female)

• β3 = difference in returns to education for women vs me

Does high R² mean model is good?

No, spurious regressions can have high R²

Does OLS require homoskedasticity for unbiasedness?

No, only for efficiency

Does adding regressors always help?

No, irrelevant regressors inflate variance and reduce adjusted R²