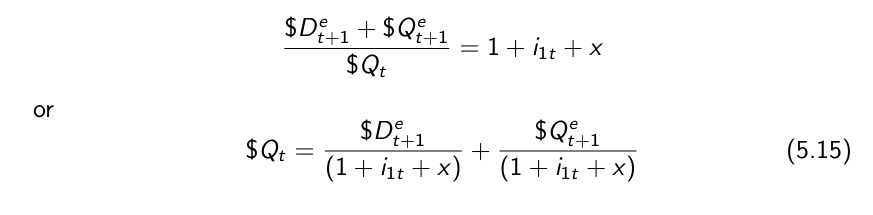Macroeconomics Expectations

Expected present discounted value

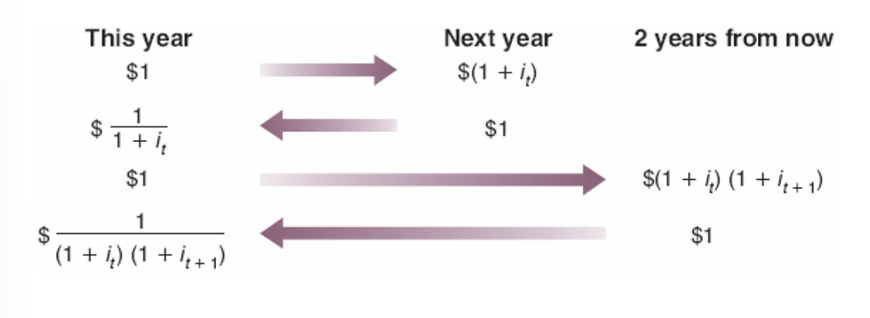
The expected present discounted value of a sequence of future payments is the value today of this expected sequence of payments.

Expected present discounted values are not directly observable, but must be constructed from information on the sequence of expected payments and expected interest rates.

1/(1 + i_t) is the discount factor with the discount rate i_t, which is used to compute the present discounted value of one dollar to be received next year.

The higher the nominal interest rate, the lower the value today of a dollar received next year.

present discounted value

present value of payments

Two ways to compute the present value of payments:

1. The present value of the sequence of payments expressed in dollars, discounted using nominal interest rates, and then divided by the price level today.

2. The present value of the sequence of payments expressed in real terms, discounted using real interest rates.

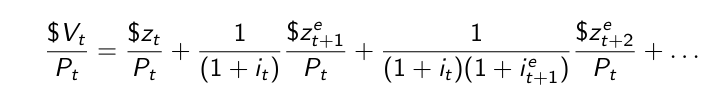
Bonds differ in two basic dimensions:

▶ Maturity: The length of time over which the bond promises to make payments to the holder of the bond.

▶ Risk:

(1) Default risk as the risk that the issuer of the bond will not pay back the full amount promised by the bond.

(2) Price risk as the uncertainty about the price you can sell the bond for if you want to sell it in the future before maturity.

Yield to maturity or yield

The interest rates associated with bonds of different maturities

Short-term interest rates

Long-term interest rates

Yields on bonds with a short maturity, typically a year or less

Yields on bonds with a longer maturity than a year

Term structure of interest rates or yield curve

The relation between maturity and yield

Types of bonds

Government bonds: Bonds issued by the government

Corporate bonds: Bonds issued by firms

Bond ratings: ratings for default risk

Risk premium: The difference between the interest rate paid on a given bond and the interest rate on the bond with the best rating

Junk bonds: Bonds with high default risk

Discount bonds: Bonds that promise a single payment at maturity called the face value

Coupon bonds: Bonds that promise multiple payments before maturity and one payment at maturity

Coupon payments: The payments before maturity

Coupon rate: The ratio of the coupon payments to the face value

Current yield: The ratio of the coupon payment to the price of the bond

Life: The amount of time left until the bond matures

Treasury bills (T-bills): U.S. government bonds with a maturity up to a year

Treasury notes: U.S. government bonds with a maturity of 1 to 10 years

Treasury bonds: U.S. government bonds with a maturity of 10 or more years

Term premium: The premium associated with longer maturities

Indexed bonds: Bonds that promise payments adjusted for inflation

Treasury Inflation Protected Securities (TIPS): Indexed bonds introduced in the US in 1997

The price of a one-year bond / a two-year bond

Arbitrage: The expected returns on two assets must be equal.

Expectations hypothesis: Investors care only about the expected returns and do not care about risk.

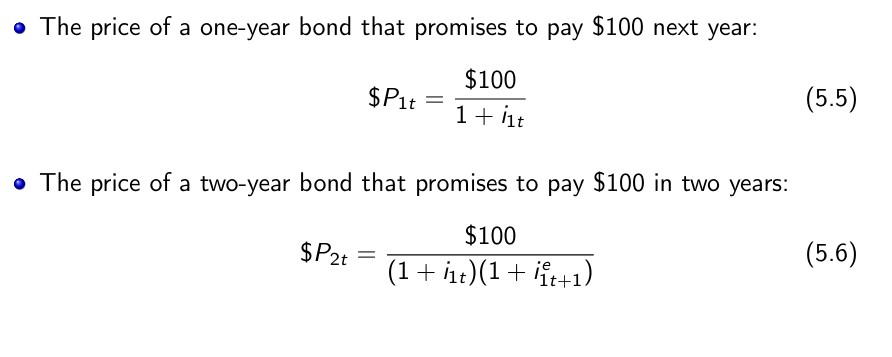
Returns from Holding One-Year and Two-Year Bonds for One Year

Two bonds must offer the same expected one-year return, which means that the price of a two-year bond today is the present value of the expected price of the bond next year.

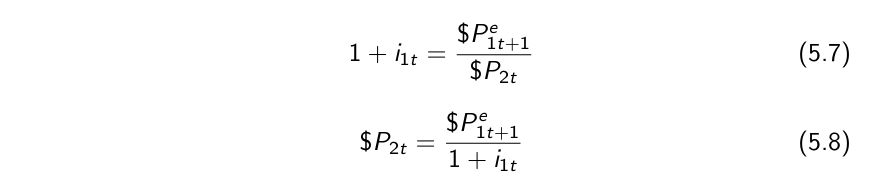
yield to maturity

The yield to maturity on an n-year bond (n-year interest rate) is the constant annual interest rate that makes the bond price today equal to the present value of future payments on the bond.

The yield to maturity on a two-year bond that satisfies

which means that the two-year interest rate is (approximately) the average of the current one-year interest rate and next year’s expected one-year interest rate.

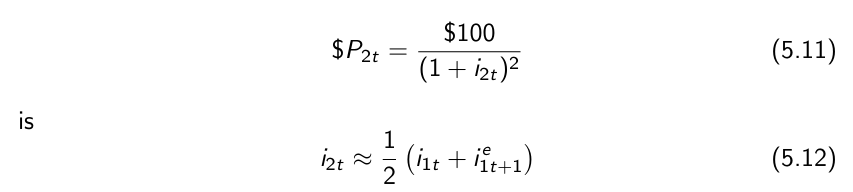
yield to maturity with a risk premium

Firms finance themselves through:

▶ Internal finance: Using their own earnings

▶ External finance: Bank loans

▶ Debt finance: Bonds and loans

▶ Equity finance: Issuing stocks or shares that pay dividends

Returns from Holding One-Year Bonds or Stocks for One Year

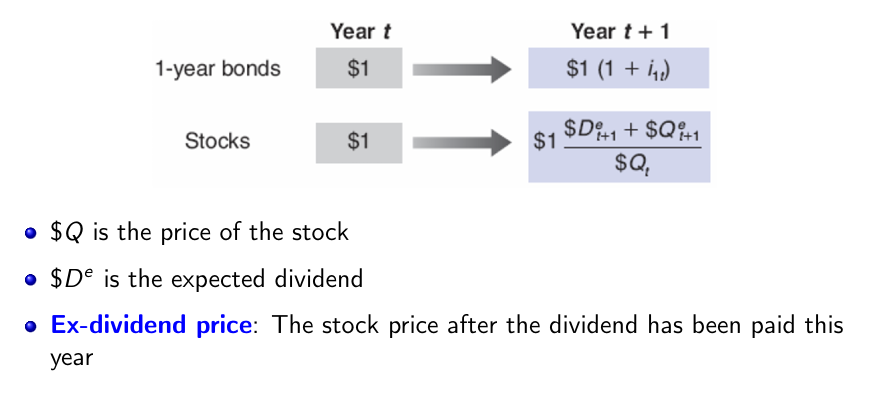
Equilibrium

Equilibrium requires that the expected rate of return from holding stocks for one year (left side) be the same as the rate of return on one-year bonds plus the equity premium x (right side):