Ch9 Public-Key Cryptography

Asymmetric Cryptography

• Uses two separate keys:

  • Public key (shared)

  • Private key (secret)

Ex: Bob wants to send Alice a message

• Bob encrypts the message with Alice’s public key

• Alice decrypts with her private key

Requirements for Public-Key Cryptosystems

1. Easy Key Generation

   • It must be computationally easy to generate a valid pair of public/private keys.

2. Easy Encryption

   • The sender, using the recipient’s public key, should be able to encrypt messages easily.

3. Easy Decryption

   • The receiver, using their private key, must be able to decrypt ciphertext easily.

4. Hard to Recover Message

   • Without the private key, it should be computationally infeasible to recover the original message from the ciphertext.

5. Hard to Derive Private Key

   • It must be computationally infeasible to derive the private key from the public key.

6. Flexible Usage

   • The system should work even if either key is used for encryption or decryption (useful for things like digital signatures).

Public-Key Cryptography for Authentication

• Sender (Bob) encrypts the plaintext using his own private key

• Anyone with Bob's public key can decrypt the message

Authentication

• If decryption using Bob’s public key works, it confirms that only Bob could’ve created the message (because only he has his private key)

What are the key principles of public-key cryptography

• Uses public/private key pairs

• Based on hard math problems

• Slower than symmetric cryptography

• No secure channel needed to share keys

• Supports digital signatures and encryption

• Commonly used in hybrid systems with symmetric ciphers like AES

RSA Public-Key Encryption

public-key cryptographic algorithm used for:

• Encrypting messages using a recipient's public key

• Decrypting messages using the matching private key

• Creating digital signatures with a sender's private key

• Verifying signatures using the sender’s public key

• Securely exchanging symmetric keys in hybrid systems

Steps of RSA

1. Key Generation

• Choose two large prime numbers: p and q

• Compute n=p×q

• Compute ϕ(n)=(p−1)(q−1)

• Choose e such that 1<e<ϕ(n) and gcd⁡(e,ϕ(n))=1

• Compute d such that d=(1 +k(ϕ(n)))/e, where k makes d a whole #

2. Public & Private Keys

• Public Key = {e,n}

• Private Key = {d,n}

3. Encryption

• Ciphertext = C = (M^e) mod n

4. Decryption

• Plaintext = M = (C^d) mod n

Types of attacks against RSA encryption

1. Brute Force – Tries all possible private keys

2. Mathematical Attacks – Attempt to factor the product of two primes

3. Timing Attacks – Exploit decryption time to reveal key info

4. Chosen Ciphertext Attacks – Use crafted ciphertexts to reveal key properties

Diffie-Hellman Key Exchange

Diffie-Hellman is not an encryption algorithm — instead, it’s a method for two parties to securely agree on a shared secret key, even if all their communication happens over a public (and insecure) channel.

• It allows two users (often named Alice and Bob) to generate a shared key independently.

• This shared key can then be used for symmetric encryption (e.g., AES).

• Its security is based on the difficulty of solving discrete logarithms, which is computationally hard.

Steps of Diffie-Hellman Key Exchange

• Global Setup (Public Values):

  • Choose a large prime number q and a base α, where α is a primitive root of q.

  • Both values are known to everyone.

• Key Generation:

  • Alice picks a private key XA​, and computes YA=α^XA mod  q — her public key.

  • Bob picks a private key XB, and computes YB=α^XB mod  q — his public key.

• Key Exchange:

  • Alice sends YA​ to Bob.

  • Bob sends YB​ to Alice.

• Secret Key Derivation:

  • Alice computes: K=YB^XA mod  q

  • Bob computes: K=YA^XB mod  q

  Both end up with the same value of K, which becomes the shared secret key.

Man-in-the-Middle Attack (Diffie-Hellman)

• An attacker intercepts and replaces the public keys during the Diffie-Hellman exchange. Each party unknowingly establishes a separate shared key with the attacker instead of with each other. This allows the attacker to decrypt, read, modify, and re-encrypt messages, compromising all communications.

• The attack succeeds because Diffie-Hellman lacks authentication.

Digital Signatures

A digital signature is like a virtual “handwritten signature” or “stamp of approval” that ensures:

• The sender is who they claim to be (authentication)

• The message has not been altered (integrity)

1. Bob wants to send Alice a message — it doesn't need to be secret, but Alice must know it really came from Bob.

2. Bob:

   • Runs the message through a hash function (e.g., SHA-512) → gets a digest

   • Encrypts the digest using his private key → this is the digital signature

   • Sends message + signature to Alice

3. Alice receives both. She:

   • Hashes the message herself (same hash function)

   • Decrypts the signature using Bob’s public key to recover the hash Bob sent

   • Compares the two hashes

Cryptographic Goals

1. Confidentiality – Ensures data is kept secret
   → Achieved with encryption (symmetric & public-key ciphers)

2. Data Integrity – Ensures data hasn’t been altered
   → Achieved with hash functions, MACs, and digital signatures

3. Authentication – Verifies the sender’s identity
   → Achieved with authentication primitives, MACs, and digital signatures

4. Non-repudiation – Prevents denial of message origin
   → Achieved with digital signatures

Non-repudiation

ensures that a sender cannot deny sending a signed message. If a message mmm and its signature s verify correctly using the sender’s public key, the sender is bound to that message. A valid signature for any different message m′≠m would break security — but this is computationally infeasible in proper schemes.

MAC

• Provides data integrity

• Provides message authentication

• Requires a shared secret key

• Sender uses key + message to generate MAC

• Receiver uses same key to verify MAC

• Ensures message is authentic and unaltered

• Does not provide confidentiality

Difference between MAC and digital signature

• Proof to third party:

  • MAC: Requires revealing the secret key

  • Digital Signature: Can be verified with public key

• Who can create it:

  • MAC: Anyone who can verify can also create

  • Digital Signature: Only private key holder can create

• Identity distinction:

  • MAC: Cannot tell who created it (shared key)

  • Digital Signature: Clearly identifies the signer

• Performance:

  • MAC: Faster, better for low-power devices

  • Digital Signature: Slower, but offers non-repudiation

HTTP vs HTTPS & Protected Segments

• HTTP:

  • Sends data in plain text

  • Vulnerable to eavesdropping

  • Only accesses the public segment of a website

• HTTPS:

  • Uses SSL/TLS for encryption

  • Secures communication over the network

  • Grants access to protected segments (sensitive data)

  • Ensures data integrity, confidentiality, and authenticity

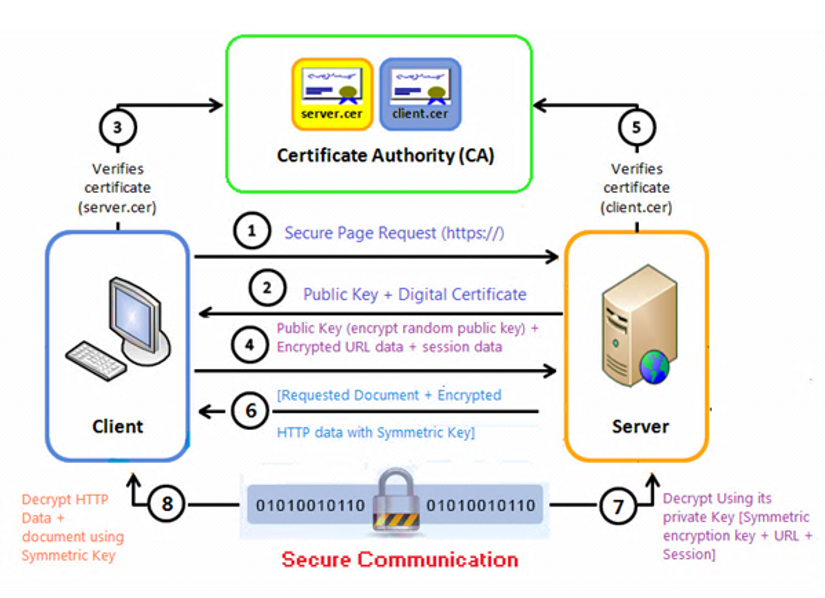
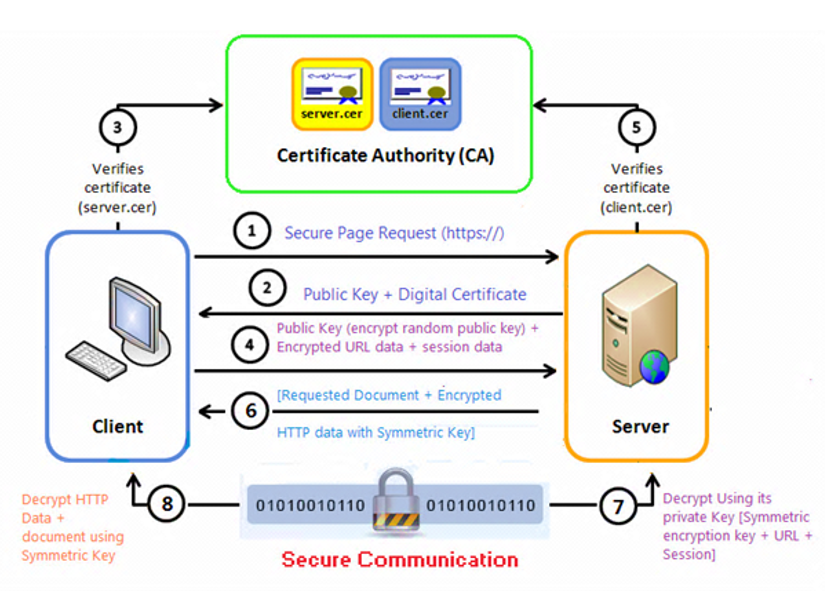
SSL/TLS Mutual Authentication Process

1. Client requests secure connection (HTTPS)

2. Server sends digital certificate

3. Client verifies server’s certificate (via CA)

4. Client sends session data encrypted with server’s public key

5. Server optionally verifies client's certificate

6. Server sends encrypted content using symmetric key

7. Client decrypts using shared symmetric key

8. Secure, encrypted communication begins

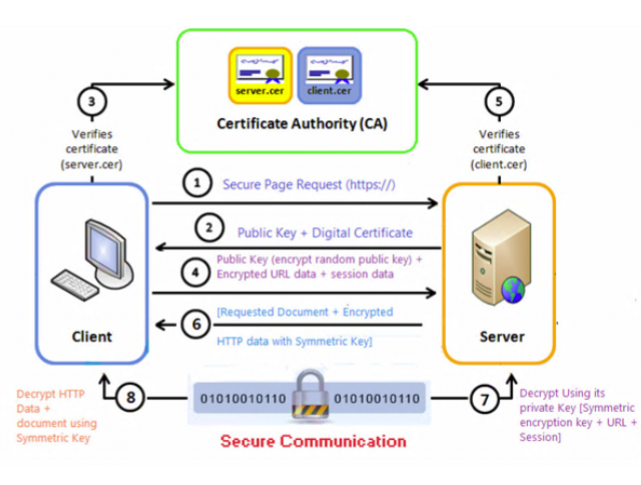
Simple description

1. You visit a website (like https://example.com)

   • Your browser asks the server to start a secure connection.

2. The server sends its public key and a digital certificate

   • The certificate is like an official ID card saying "I am really example.com".

3. Your browser checks the server's certificate

   • It checks if the server's ID is valid and trustworthy by looking at known Certificate Authorities (CAs).

4. Your browser creates a random "secret password" (session key)

   • It locks (encrypts) this secret with the server’s public key and sends it to the server.

   • Only the server can open this, because only the server has the matching private key.

5. The server (optional) checks the client’s certificate

   • This is rare and usually only for special cases where the server wants to know exactly who the client is (like in banks).

6. Now both sides have the same secret key (session key)

   • They can start sending information back and forth using this shared secret key, which is fast and secure.

7. The server uses its private key to open the secret password you sent

   • Now both of you know the same secret key and can start secure communication.

8. Your browser and the server now talk privately

   • Every message is locked with the shared key, and both sides can unlock it easily, but no one else can.

Public-Key for Certified Authority

Receives certificate request containing the public key

Verifies the requester’s identity

Signs the public key with CA’s private key

Issues a digital certificate to the requester

Allows others to trust the public key using CA’s public key