Indexed Retrieval

Keys

a unique name/identifier for each object

allows a set of objects/records to be stored in sorted order, so binary search can be used for retrieval

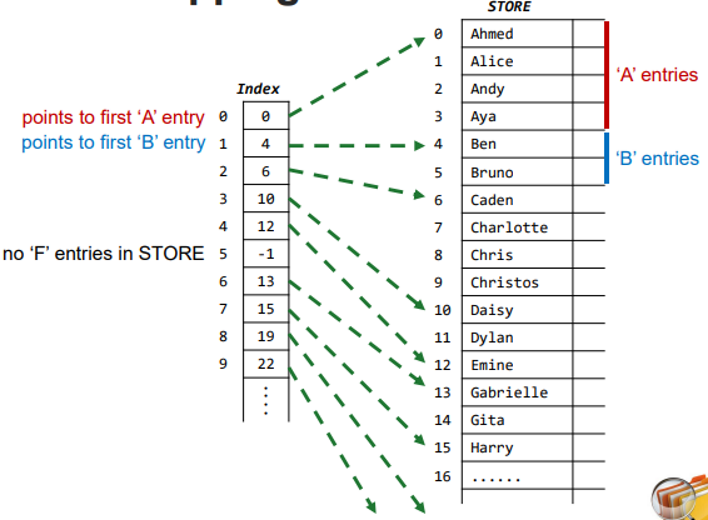
Keys into Indexes

an array can be constructed to index the first element of each section

if there are no keys with a specific letter then index[n] = -1

The Index Mapping

Pseudocode for Index Retrieval with a Linear Search

given name, look for record in STORE with matching key:

take first letter L from name;
convert L to numeric value V;
P = Index[V];
if (P < 0) then no records start with letter L -> fail
while (first letter of key of STORE[P] == L)
{
	if (key == name) //record found
	{
		return STORE[P];
	}
	P++; //move to next record
} //if loop exhausts, name wasn't found

Efficiency of Index Retrieval with Linear Search

linear search of the section starting at STORE[P] 

Worst case:

•  All keys start with same letter – all records are in the same section: 

• linear search through the whole array; O(N)

In practice: 

• Depends on the size of sections (for each letter); if all sections are roughly equal size, it can be up to 26x faster than linear search without indexing

• Of course, because some names beginning with some letters are more common than others, the gain will be probably smaller

Efficiency of Indexed Retrieval with Binary Search

if some of sections are large, we can do a binary search of the section starting at STORE[P] 

Worst case: 

• Everything in one section: binary search whole array, O(log2N) 

In Practice: 

• Depends on the size of sections, but could be up to 26x times faster than binary search without indexing.

Collision-Free Storage Algorithm

given name, look for record in STORE with matching key:

take first letter L from name;
convert L to numeric value V;
if (STORE[V].key == name)
{
	return STORE[V]; //record found
}
else ... //no matching key

note that only one element of STORE is tested, hence fast constant time O(1)

Dealing with Collisions using Indexed Retrieval

• put keys into a sorted array

• use an index array to find relevant section 

• but to insert extra data, the index array must be recomputed

Dealing with Collisions using Linked Lists

For storage based on first letter of each key: 

use a linear array STORE of 26 elements representing the alphabet with each element pointing to the appropriate chain; i.e. STORE[0] points to a chain of objects whose keys starts with ‘A’ 

Indexed Retrieval Algorithm using Linked Lists

given name, look for record in STORE with matching key:

take first letter L from name;
convert L to numeric value V;
obtain chain pointer P from STORE[V];
while (P != null)
{
	if (P.key == name) //record found
	{
		return P;
	}
	P = P.next; //move to next record
} //if loop exhausts, name wasn't found

Worst Case of Dealing with Collisions using Linked Lists

• Every object is on the same chain 

• Like linear search, O(N) 

Practicality of Dealing with Collisions using Linked Lists

Much faster – if the objects are distributed across many chains, so same improvement as with using arrays

Advantages of Dealing with Collisions using Linked Lists

• Chains are dynamic, so extra objects can be inserted more easily

• No need to recompute index