Astigmatism

In this session you will expand your knowledge about refraction and lenses to the topic of cylindric/toric lenses and astigmatism (e.g., the Jackson Cross cylinder (JCC) that you use in subjective refraction is a toric lens).

Sphere vs Toric Shape - Introduction

• A spherical shape (e.g. football) has the same radius at all meridians (0 degree to 360 degree).

• A toric shape (e.g. rugby ball) has different radii along individual meridians with the shortest radius being perpendicular to the longest radius.

A spherical shape has the same _____ at all meridians .

Radius

Toric or Cylindric Shape

• Axis of rotation (YY’) lies between the vertex (A) of the generating arc and its centre of curvature (C_T).

Barrel

• The barrel formation gives good off axis performance but is not particularly suited for mass production of lenses.

• YC_EY’ = axis of rotation

• DD’ = generating arc (meridian1) and CC’ = meridian 2 (perpendicular to meridian 1)

• C_T = centre of curvature of the generating arc

• A = vertex of the generating arc

The barrel formation gives good off axis performance but is not particularly suited for mass ______ of lenses.

Production

Toric or Cylindric Shape

• Axis of rotation (YY’) and the vertex (A) of the generating arc lie on opposite sides of the centre of curvature (CT).

Tyre

• The tyre formation lends itself to mass production and consequently, it is the most common surface found on standard ophthalmic lenses

• YC_EY’ = axis of rotation

• DD’ = generating arc (meridian1) and CC’ = meridian 2 (perpendicular to meridian 1)

• C_T = centre of curvature of the generating arc

• A = vertex of the generating arc

The _______ lends itself to mass production and consequently, it is the most common surface found on standard ophthalmic lenses.

Tyre Formation

Toric or Cylindric Shape

• Concave in one principal meridian (DD’) • Convex in second principal meridian (CC’)

• Axis of rotation (YY’) and centre of curvature (CT ) of the generating arc lie on opposite sides of the vertex (A)

CAPSTAN

• The capstan formation is rarely used in ophthalmic lenses (sometimes for solid bifocals)

• YC_EY’ = axis of rotation

• DD’ = generating arc (meridian1) and CC’ = meridian 2 (perpendicular to meridian 1)

• C_T = centre of curvature of the generating arc

• A = vertex of the generating arc

The _______ is rarely used in ophthalmic lenses (sometimes for solid bifocals)

Capstan Formation

Toric or Cylindric Shape

• Plano in one principal meridian (DD’)

• Convex in the second principal meridian (CC’)

Plano-Convex Cylinder

• YC_EY’ = axis of rotation

• DD’ = generating arc (meridian1) and CC’ = meridian 2 (perpendicular to meridian 1)

• C_T = centre of curvature of the generating arc

• A = vertex of the generating arc

Convex is the _______ principal meridian.

Second

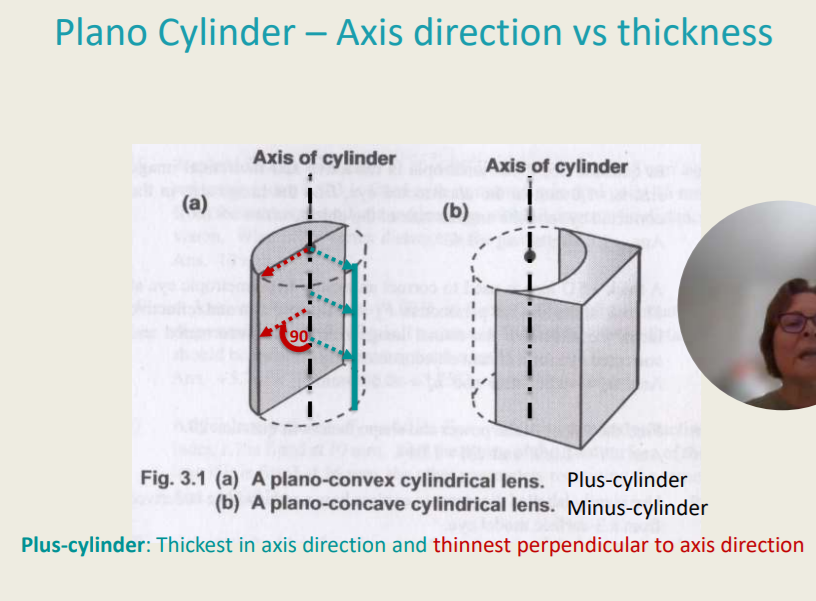
Plano Cylinder - Axis Direction vs Thickness

• Plus-cylinder: Thickest in axis direction and thinnest perpendicular to axis direction

• A plano-convex cyclindrical lens (Plus-cylinder)

• A plano-concave cylindrical lens (Minus-cylinder)

• Plus-cylinder: Thickest in axis direction and thinnest perpendicular to axis direction

• Minus-cylinder: Thinnest along axis direction and thickest perpendicular to axis direction.

A plano-convex lens is a _________ and a plano-concave lens is a _______.

Plus-cylinder; Negative-cylinder

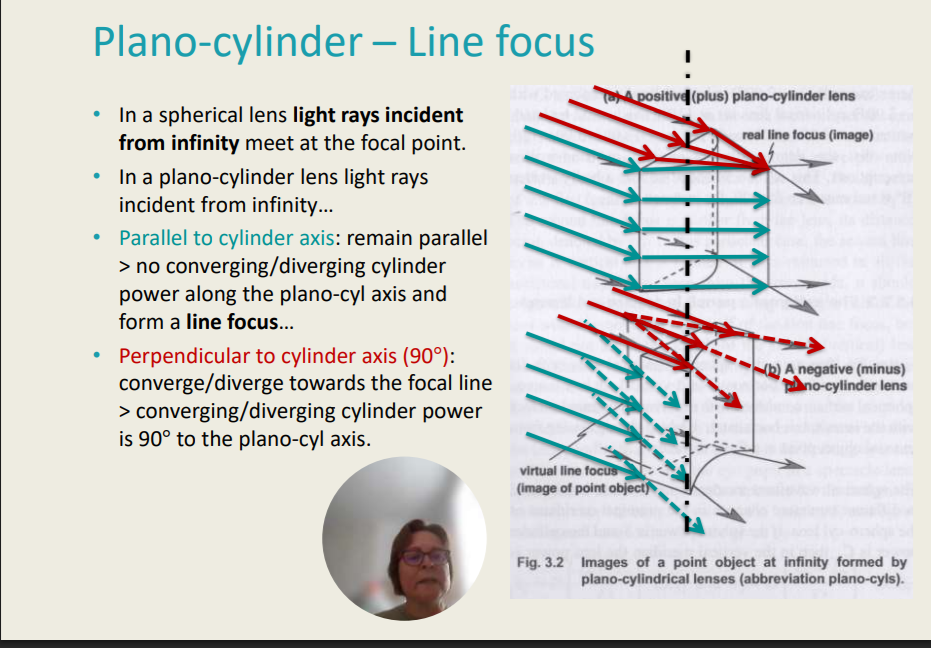
Plano-Cylinder - Line Focus

• In a spherical lens light rays incident from infinity meet at the focal point.

• In a plano-cylinder lens light rays incident from infinity…

• Parallel to cylinder axis: remain parallel > no converging/diverging cylinder power along the plano-cyl axis and form a line focus

• Perpendicular to cylinder axis (90°): converge/diverge towards the focal line > converging/diverging cylinder power is 90° to the plano-cyl axis

Parallel to cylinder ax is __________________ and perpendicular to cylinder axis is ______________.

Not a converging/ diverging cylinder power; Converging/ diverging cylinder power

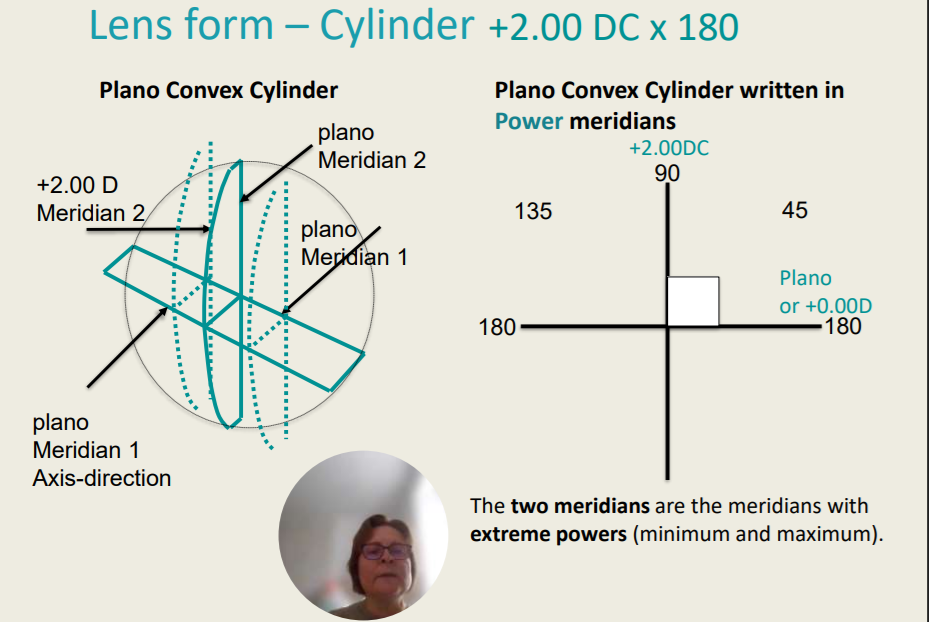
The two meridians are the meridians with extreme powers __________.

Minimum and Maximum

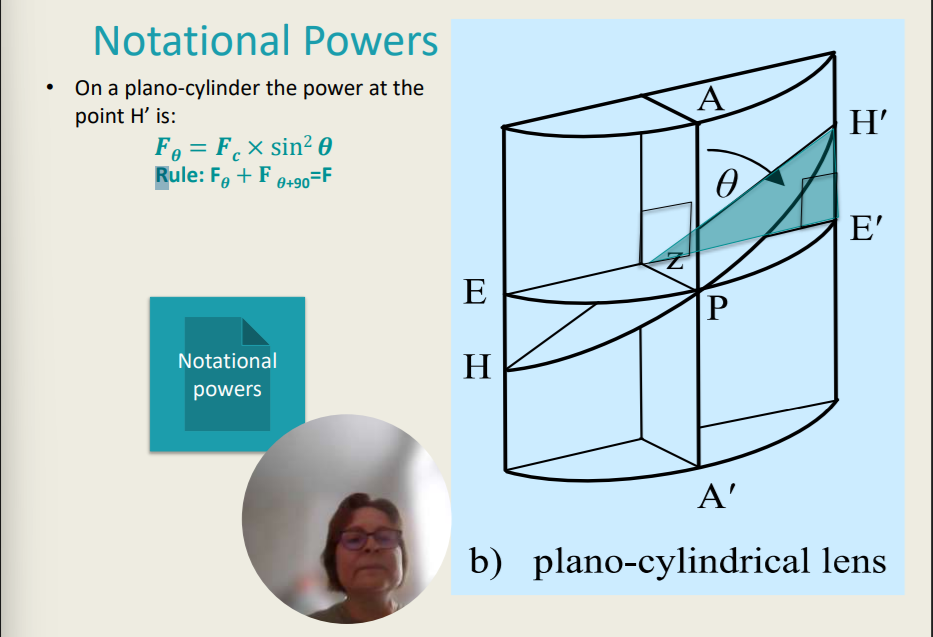
Notational Powers

• On a plano-cylinder the power at the point H’ is:

• 𝑭𝜽 = 𝑭𝒄 × sin2 𝜽

• Rule: F𝜽 + 𝐅 _𝜽+90 = F

On a _________ the power at the point H’.

Plano-cylinder

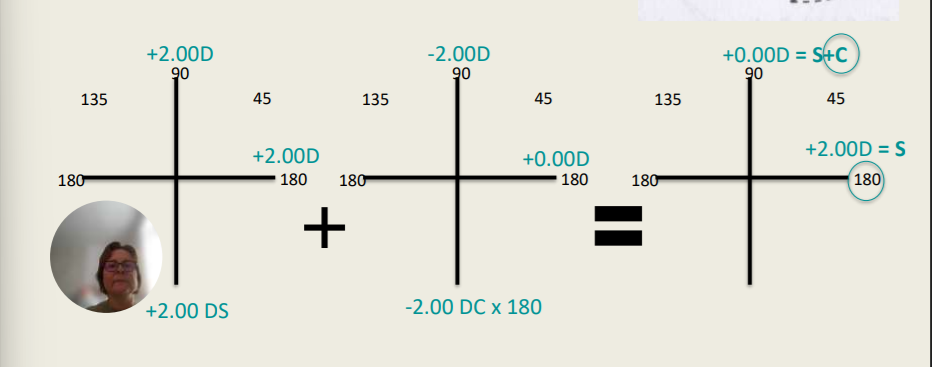
General Cylindrical Lenses

• Can be seen as a plano- convex=plus (or planoconcave=minus) spheric lens glued on to a planoconcave=minus (or plano-convex=plus) cylindrical lens.

• Hereby all combinations between spherical and cylindrical lens is possible.

See pictures. What is the final calculation?

+0.00DC; +2.00DS

Sphero-cylindrical Combination Power

• cylinder effect (power) in 90°

• In cylinder direction only sphere has effect 180°

See picture. What is the final calculation?

+2.00DS; +0.00DC

Sphero-cylindrical Combination Directions

• +2.00 DS/ -2.00 DC x 180° is named sphero-cylindrical combination and indicates the cylinder axis direction.

• The writing used in the picture refers to as “Minus-cylinder writing”.

• Clear lines in a focimeter indicate the direction of the cylinder axis.

• The lens is thinnest in the direction of the minus-cyl axis: 180°

• There is another way to write exactly the same relationship: ‘plus-cylinder writing

The writing used in the picture refers to as “_________ writing”.

Minus-Cylinder

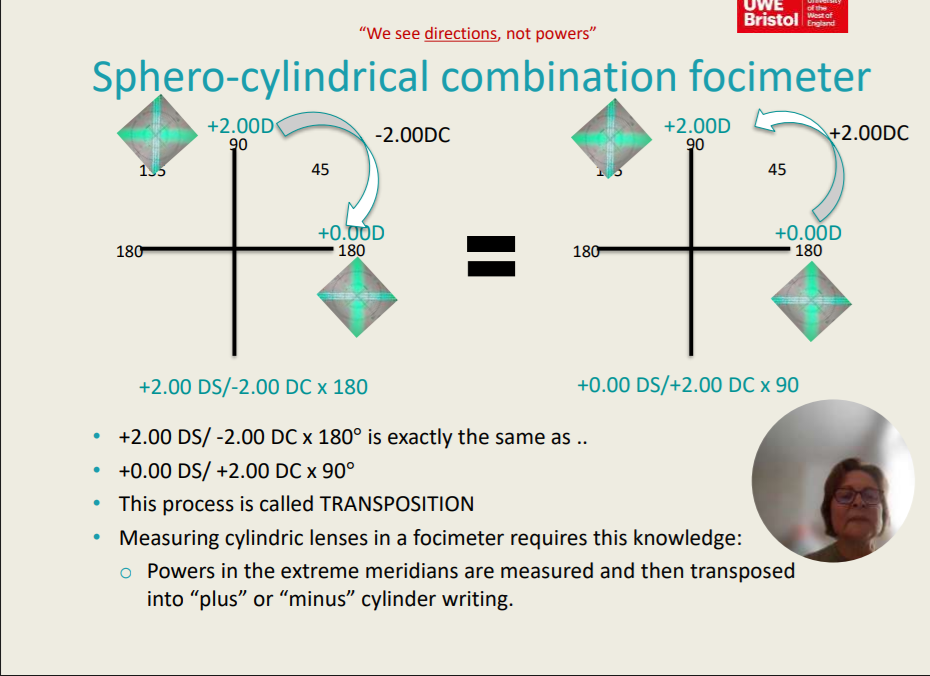
Sphero-cylindrical Combination Focimeter

• +2.00 DS/ -2.00 DC x 180° is exactly the same as ..

• +0.00 DS/ +2.00 DC x 90°

• This process is called TRANSPOSITION

• Measuring cylindric lenses in a focimeter requires this knowledge:

  • Powers in the extreme meridians are measured and then transposed into “plus” or “minus” cylinder writing.

Powers in the _______ are measured and then transposed into “plus” or “minus” cylinder writing.

Extreme Meridians

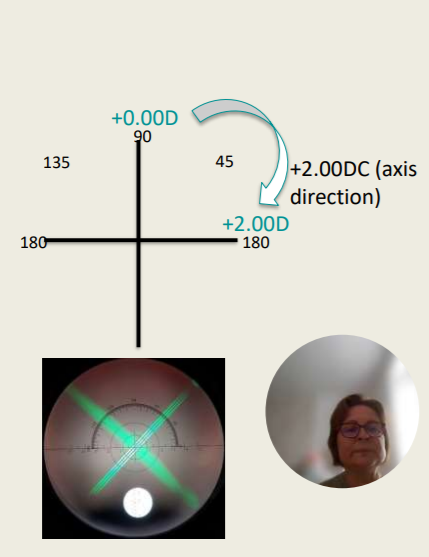
Transposition Scheme ‘+’ Cyl

• Sphere: least positive meridian power

• + Cyl: the most positive minus the least positive meridian power

• Axis: the axis of the most positive meridian

• Example:

  • Sphere: +0.00 DS

  • +Cyl: +2.00 – 0.00= +2.00 DC

  • Axis: 180

• Application: Focimetry

• The lines are clear along the meridian axis.

_______ ia the least positive meridian power.

Sphere

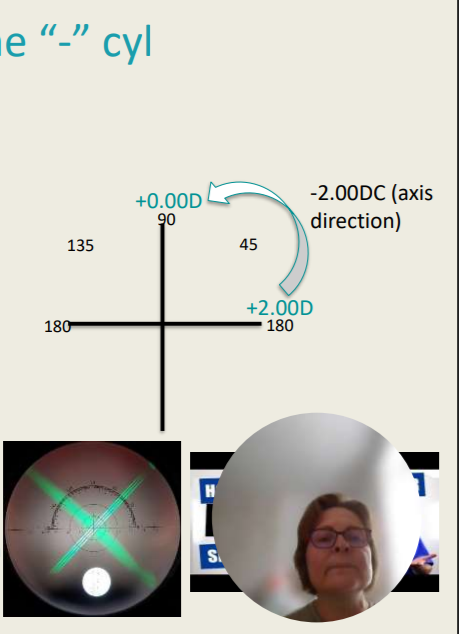
Transposition Scheme ‘-’ Cyl

• Sphere: most positive meridian power

• - Cyl: the least positive minus the most positive meridian power

• Axis: the axis of the least positive meridian

• Example:

  • Sphere: +2.00 DS

  • +-Cyl: +0.00 – (+2.00)= -2.00 DC

  • Axis: 90

• Application: Focimetry!

• The lines are clear along the meridian axis.

-Cyl is the ___________ the most positive meridian power.

Least Positive Minus

Transposition ‘+’ to ‘-’ Cyl

• transposed sphere (DS): Add DS to DC

• Transposed axis: is perpendicular to old axis

  • If old axis between 0 and 90: add 90

  • If old axis is between 91 and 180: deduct/subtract 90 degree

• Transposed cyl (DC): change the sign of DC

• Example:

  • +0.00DS + (+2.00 DC) = +2.00 DS

  • 180-90= 90

  • +2.00DC becomes -2.00 DC

+0.00 DS/+2.00 DC x 180 ← → +2.00 DS/-2.00 DC x 90

This is transposition ‘+’ to ‘-’ cyl.

Examples Transposition

• One power reading where lines of focimeter are clear is -0.75D/45 and the second power reading where the perpendicular lines are clear is +0.75/135

  • What is the sphero-cylindrical combination in minus-cylinder writing?

  • Transpose the result into plus-cylinder writing.

• One power reading where lines of focimeter are clear is +1.25D/5 and the second power reading where the perpendicular lines are clear is +0.75/95

  • What is the sphero-cylindrical combination in minus-cylinder writing?

  • Transpose the result into plus-cylinder writing.

Problem 1

• Minus - Cylinder Writing

  • Sphere: most positive meridian power (+)

    • +0.75DS

  • - Cyl: the least positive minus the most positive meridian power ([-] - [+])

    • -0.75D - (+0.75D) = -1.50DC

  • Axis: the axis of the least positive meridian (-)

    • 45 degrees

Final Answer = +0.75DS / -1.50DC x 45

• Plus - Cylinder Writing

  • Sphere: the least positive meridian (-)

    • -0.75D

  • +Cyl: the most positive meridian minus the least positive meridian ([+] - [-])

    • +0.75 - (-0.75D) = +1.50D

  • Axis: the axis of the most positive meridian (+)

    • 135 degrees

Final Answer = -0.75DS / +1.50DC x 135

Problem 2

• Minus - Cylinder Writing

  • Sphere: most positive meridian power (+)

    • +1.25DS

  • -Cyl: least positive minus the most positive meridian ([-] - [+])

    • +0.75D - (+1.25D) = -0.50DC

  • Axis:the axis of the least positive meridian (-)

    • 95

Final Answer = +1.25DS / - 0.50DC x 95

• Plus - Cylinder Writing

  • Sphere: least positive meridian power (-)

    • +0.75D

  • + Cyl: the most positive minus the least positive meridian power ( [+] - [-])

    • +1.25D - (-0.75D) = +2.00D

  • Axis: the axis of the most positive meridian (+)

    • 5

Final Answer = +0.75DS / +2.00DC x 5

Example Transposition

• One power reading where lines of focimeter are clear is -3.00D/25 and the second power reading where the perpendicular lines are clear is -1.75/115

  • What is the sphero-cylindrical combination in minus-cylinder writing?

  • Transpose the result into plus-cylinder writing.

• 4. One power reading where lines of focimeter are clear is -2.25D/160 and the second power reading where the perpendicular lines are clear is -1.5/70

  • What is the sphero-cylindrical combination in minus-cylinder writing?

  • Transpose the result into plus-cylinder writing.

Try to work the Calculations. What is the answer?

Problem 1

Minus-Cylinder Writing

• Sphere: the most positive (-1.75D)

• -Cyl: least positive - most positive (-3.00 - [-1.75]) = -1.25

• Axis: the least positive (25)

Final Answer = -1.75DS / -1.25DC x 25

Plus-Cylinder Writing

• Sphere: the least positive (-3.00D)

• +Cyl: most positive - least positive (-1.75D- [-3.00]) = +1.25D

• Axis: the most positive (115)

Final Answer = -3.00DS / +1.25DC x 115

Problem 2

Minus - Cylinder Writing

• Sphere: the most positive (-1.50D)

• -Cyl: least positive - most positive (-2.25 - [-1.50]) = -0.75D

• Axis: least positive (160)

Final Answer: 1.50DS / -0.75DC x 160

Plus - Cylinder Writing

• Sphere: the least positive (-2.25D)

• +Cyl: most positive - least positive (-1.50 - [-2.25]) = +0.75D

• Axis: most positive (70)

Final Answer = -2.25DS / +0.75DC x 70

Sturm’s Conoid - Image position and Image Sizes

• The line focus associated to the 90° meridian is along the 180 ° axis. For an image formed from an object in infinity.

• The line focus associated to the 180° meridian is along the 90 ° axis. For an image formed from an object in infinity.

  • TB= height object

  • LR=horizontal size object

  • L1’= vergence produced by power 90°

  • L2’= vergence produced by power 180°

• Disc of Least Confusion (DoLC) - also circle of least confusion Size: DoLC = TB x (L1’-L2’) / (L1’ +L2’)

• Size of line of foci 1: LF1 = LR x ((L1’- L2’) / L1’)

• Position DoLC: L_DoLC’ = (L1’ + L2’) / 2

• Size line of foci 2: LF2 = TB x ((L1’ - L2’) / L2’)

The line of focus associated with the 90° meridian is along the _______ axis.

180 °

An Astigmatic Eye - Best Sphere

• If you refract an eye with astigmatism, the first step is to find the “Best sphere” by using spherical lenses

• This is when the Disc of least Confusion (DoLC) lies at the retina

If you refract an eye with astigmatism, the first step is to find the “_______” by using spherical lenses.

Best Sphere

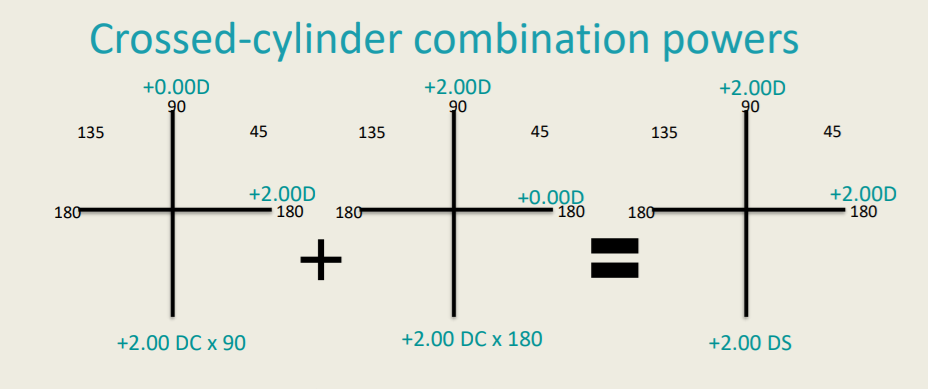
Crossed-Cylinder Combination Powers

• If two plus-cylinders (or minus cylinders) of the same power are added 90 degree perpendicular to each other, the result is a spherical lens of the power of these cylinders.

If two plus-cylinders (or minus cylinders) of the same power are added 90 degree perpendicular to each other the result is a ___________ lens of the power of those cylinders.

Spherical

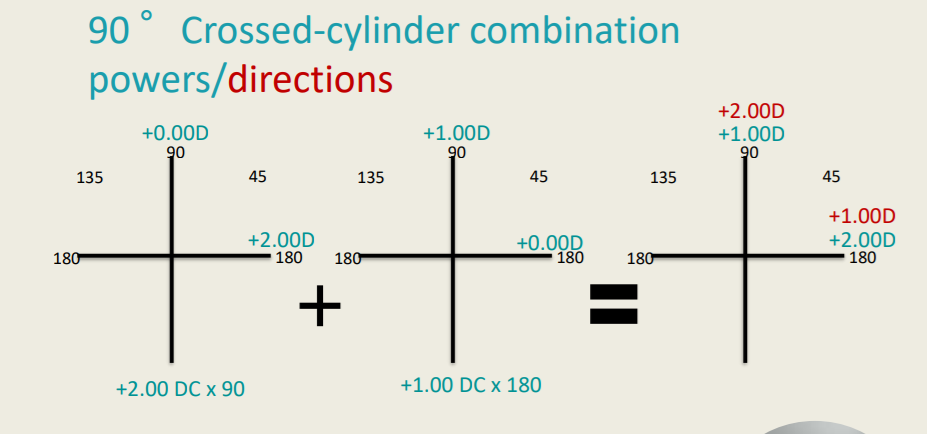
90° Crossed-cylinder Combination Powers/Directions

• Sphero-cylindrical combination is easy determined based on axis directions:

  • +2.00DS/-1.00DC x 180 OR +1.00DS/+1.00DC x 90

Come back to figure how to calculate this.

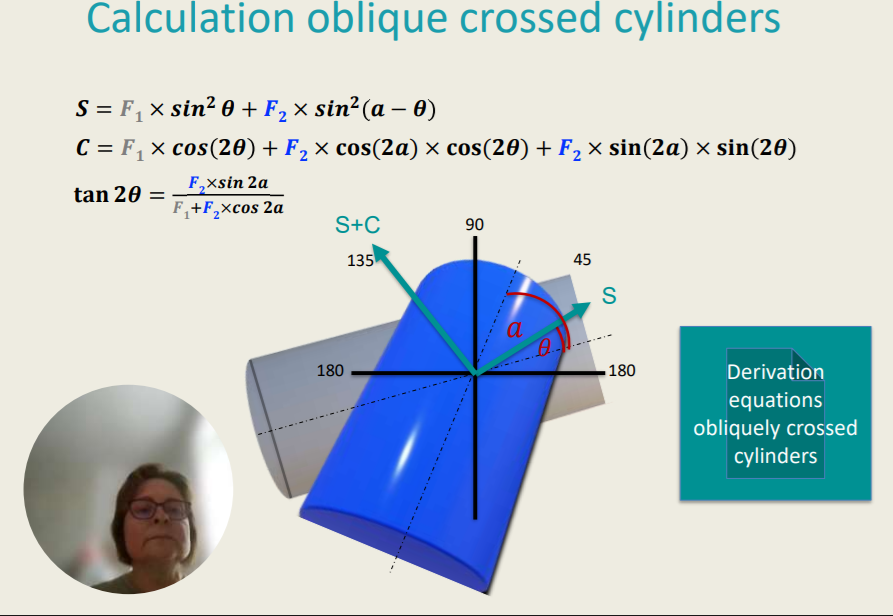
Oblique Crossed Cyinders

• If two cylinders are crossed at an angle ≠ 90°.

• An application of this is the “Stoke lens” in an autorefractor. It consists of two planocylinder lenses with equal magnitude plusand minus powers. The plano surfaces are mounted to be rotated in opposite directions.

• An implication of it is, that if the patient is not corrected in the exact axis position (i.e. subjective refraction, retinoscopy in astigmatism) a new cylinder will be produced (which is hardly predictable without calculation).

• 𝑺 = 𝑭𝟏 × 𝒔𝒊𝒏^𝟐 𝜽 + 𝑭𝟐 × 𝒔𝒊𝒏^𝟐 (𝒂 − 𝜽 )

• 𝑪 = 𝑭𝟏 × 𝒄𝒐𝒔 (𝟐𝜽) + 𝑭𝟐 × 𝐜𝐨𝐬(𝟐𝒂) × 𝐜𝐨𝐬(𝟐𝜽) + 𝑭𝟐 × 𝐬𝐢𝐧 (𝟐𝒂) × 𝐬𝐢𝐧 (𝟐𝜽)

• 𝐭𝐚𝐧 𝟐𝜽 = 𝑭𝟐 × 𝒔𝒊𝒏 𝟐𝒂 / 𝑭𝟏+𝑭𝟐 ×𝒄𝒐𝒔 𝟐𝒂

If the patient is not corrected in the exact axis position a new cylinder is produced. True or False?

True

The Jackson Cross- Cylinder

• A toric lens with the power meridians of the same magnitude, but plus and minus powers.

• L_CoLC’=0D (at the retina)

• Cylinder power of the example: -1.00 DC

• Sphero-cylindric combination of ±0.50𝐷 is +0.50 DS/- 1.00 DC

• If placed before an eye with minus-cyl axis in axis direction of the correcting minus-cyl it adds +0.50 DS and -1.00 DC in the eyes’ axis direction.

• If placed before an eye with minus-cyl axis perpendicular to axis direction of the correcting minuscyl it deducts +0.50 DS and -1.00 DC in the eyes’ axis direction.

• If flipped between in and perpendicular axis direction it adds or deducts -0.50 DC; depending on which position was clearer you will add or subtract -0.50 DC

The Jackson Cross-Cylinder is a _______ with the power meridians of the same magnitude, but plus and minus powers.

Toric Lens

Need to Know:

• Types of toric surfaces: barrel, tyre (most common toric surface), capstan

• Thickness toric lenses: plus-cylinder – thickest in axis direction; minus-cylinder - thickest perpendicular to axis direction

• Converging/diverging cylinder power is perpendicular (90°) to the cylinder axis.

• Sphero-cylindrical combination:

  • is how we write cylindric/toric lenses; can be written in plus- or minus-cylinder writing; the conversion from one to another is called transposition.

  • Has two extreme powers – one along and one perpendicular to cylinder axis; the powers in meridians between are “notational” powers

• Circle of least confusion: in refraction “best sphere”

• Jackson Cross-cylinder: ± 0.25 means a sphero-cylindrical combination of +0.25DS/- 0.50DC/axis along red line; flipping means a change of 0.25DC and placing before an eye vs taking it away means a change of +0.25DS/-0.50DC/axis (adding or deducting depending on where the minus axis is placed relative to the cylinder axis of the eye)

Converging/diverging cylinder power is _________ (90°) to the cylinder axis.

Perpendicular

Think for Yourself

How would you explain to a patient…

• A patient enters your practice and complains about the pair of spectacles s/he just had collected. Checking the prescription with the focimeter measurements shows that both values are in agreement. You carry out a refraction and, you find that the 1.75 D cylinder axis of the RE is by 10 degrees different from the one of your colleague. However, with your refraction results the patient vision is much better and more comfortable.

  • Besides the cylinder axis, which other components will be altered?

  • Explain to the patient what has happened during the previous refraction.

When the cylinder axis changes significantly (even by 10° with a moderate-to-high cylinder like 1.75 D), it doesn't just alter the axis — it also affects:

• The effective sphere power along the principal meridians.

• The effective cylinder at various meridians.

• The optical quality and orientation of the correcting lens.

• The location of the blur circle or image distortion.

This is because the spherocylindrical combination behaves differently when the axis rotates, especially with higher cylinders. So, even if the focimeter confirms that the prescription was filled correctly, a 10° axis error can cause significant discomfort, distortion, or blurred vision.

Thank you for coming in — I can understand how frustrating it must be to have new glasses that just don’t feel right. I’ve checked the glasses you were given, and they were made correctly according to the prescription. But when I rechecked your eyes today, I found that while most of your prescription matches, there’s a small difference in the orientation of one part of your lens — the cylinder axis — in your right eye.

The cylinder part of your glasses helps correct the astigmatism, which is like a difference in focus between different angles. Imagine trying to read a line that’s tilted the wrong way — it can look blurry or off. Even a small angle change can make your vision feel off-balance or strained, especially with stronger astigmatism like yours.

With the new axis we measured today, your vision was much clearer and more comfortable, which tells us that your eyes are sensitive to that orientation. It’s not unusual — small angle errors can make a big difference for some people.

I recommend we update your glasses with this new correction so you can get the clarity and comfort you need.