6-The electric potential

What is the expression for work done by an external force to move a charge q in an electric field E?

ds= the displacement element along the path.

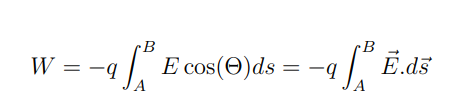
What is the significance of the dot product E⋅ds in the work done equation?

It ensures that only the component of the electric field along the displacement contributes to the work done.

Why is the work done independent of the path taken?

• The work is the same for any path because the electric field is conservative.

• This means the work depends only on the initial and final positions, not on the path taken.

How can you visualise path independence in an electric field?

Any path can be decomposed into:

1. Circular arcs perpendicular to E → No work done.

2. Radial sections parallel to E → Same work as the straight-line path.
   

   Thus, work is independent of the path.

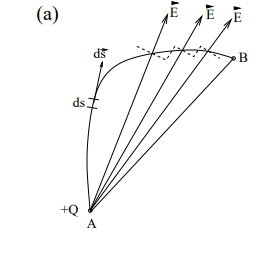
What does it mean for the electric force to be conservative?

• It means that the work done in moving a charge between two points is independent of the path taken

• The total work done in a closed loop is zero.

What does path independence imply in the context of electric fields?

Path independence means that the work done in moving a charge qqq between two points is the same, regardless of the path taken, as the electric field is conservative.

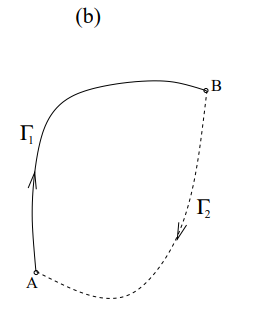
What is the result when the work done along two different paths Γ_1​ and Γ₂​ is considered?

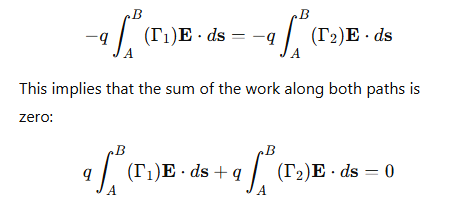
What is the Circuital Law?

• The Circuital Law states that the line integral of the electric field along any closed path is zero

• This applies to static electric fields.

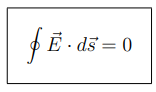
What does the circle in the notation ∮E⋅ds represent?

It indicates that the integral is taken along a closed path

What is the difference between the circuital law and Gauss’s law?

• The circuital law is a line integral around a closed path for a static electric field.

• Gauss’s law involves a surface integral over a closed surface related to the electric flux.

What are Gauss’s Law and the Circulation Law equivalent to?

Gauss’s Law and the Circulation Law together are equivalent to Coulomb’s Law in electrostatics.

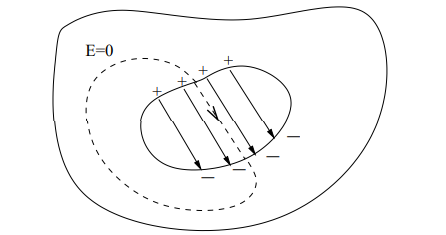
What is the electric field inside a hollow conductor?

The electric field inside a hollow conductor is zero, regardless of the conductor's shape.

Why is the electric field inside a hollow conductor zero?

Because all excess charge resides on the outer surface, and there is no charge on the inner surface.

What happens if there were both positive and negative charges on the inner surface of the hollow conductor?

• It would lead to a non-zero circulation of the electric field

• This would violate the Circulation Law ∮E⋅ds=0

What does the electric potential represent?

The electric potential at a point is the potential energy per unit charge at that point in an electric field.

How is the work done in moving a charge related to the potential energy?

• The work done in moving a charge q from point A to point B is equal to the change in potential energy of the charge.

• This is path-independent.

What is the expression for potential energy at point B?

• Γ is any path from A to B.

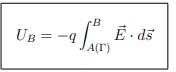
What is the definition of electric potential V_B at point B?

This is valid for any path between A and B.

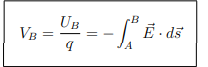
What are the units of electric potential V?

Volts

How does the superposition principle apply to electric potential?

It states that the electric potential at a point due to multiple charges is the algebraic sum of the potentials due to each individual charge.

What is the formula for potential difference (p.d.) between two points B and C?

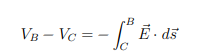
What is the significance of the potential difference between two points?

It represents the work needed to move a unit charge from one point to another

What is the reference point for electric potential around a point charge?

It is conventionally taken to be at infinity, where the potential is defined as zero.

What is the formula for the electric potential at a distance R from a point charge Q?

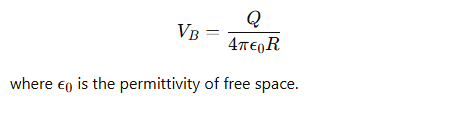
What is an equipotential surface?

• Its a surface where all points have the same electric potential.

• No work is required to move a charge along this surface.

What is the relationship between the electric field and equipotential surfaces?

• The electric field is always perpendicular to an equipotential surface at every point.

• No work is done when a charge moves along an equipotential because the electric field does no work in that direction.

What happens to the potential when the electric field is zero?

• When the electric field is zero, the potential must be constant.

• This is true for any region with no electric field, such as inside a conductor.

Why are conducting surfaces equipotential surfaces?

Because the electric field inside a conductor is zero in electrostatic equilibrium, meaning the potential must be constant throughout the conductor.

What can we deduce about the electric field just outside a conductor?

• The electric field just outside a conductor must be perpendicular to the surface because the conductor is an equipotential surface

• The electric field must be normal to equipotential surfaces.