Chapter 3 Theorems/ideas - Matrix Algebra

Theorem 3 - Row operations on Determinants

Let A be a n x n matrix:

• adding a multiple of one row to another does not change det A

• Swapping two rows multiplies det A by -1

• Multiplying a row by k multiples detA by k

Find det efficiently → row reduce, track swaps & scaling’s

Theorem 4 - Invertibility via Determinant

A is invertible ←> det A doesn’t = 0

Guarantees:

• Zero determinant = no inverse

• Links directly to the IMT

Theorem 5 - Determinant of a Transpose

det(A^T) = det(A)

Lets you freely switch rows and columns in determinant arguments

Theorem 6 - Determinant of a Product

det(AB) = (detA)(detB)

Guarantees:

• If either matrix is singular - product is singular

• Used heavily in linear transformation arguments

Theorem 7 - Cramer’s Rule

If A is invertible and Ax = b, then:

where A_i(b) replaces column i of A with b

• Mostly conceptual, not computational

  • Signals unique solution

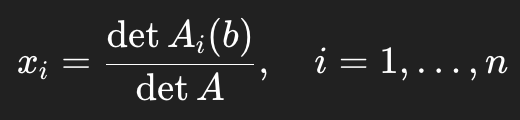
Theorem 8 - inverse via Adjugate

If A is invertible,

Guarantees:

• Inverse exists only if det A doesn’t = 0

• adjA = transpose of co-factor matrix

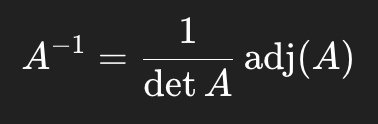
Theorem 9 - Determinant as Area / Volume

For 2 × 2 matrices:

|det A| = area of the parallelogram formed by columns

For 3 × 3 matrices:

|det A| = volume of the parallelpiped

• Determinant measures geometric scaling

Theorem 10 - Determinant & Linear Transformations

If T(x) - Ax then:

“What does det mean geometrically?” → scaling factor

Determinant of a Triangular Matrix

For triangular matrices:

det A = product o diagonal entries

After row reduction, stop immediately

Zero Row → Zero Determinant

If A has a row or column of all zeros, then:

det A = 0

Also, if the rows are identical or linear dependent or the matrix is not invertible

• Its a loss of dimension

Guarentee:

• Matrix is singular

• No Inverse