2-way ANOVA

When is a 2-way ANOVA used?

when the dependent variable is a single continous variable; when the independent variables are categorical variable (2 variables each with 2 or more groups)

Full Factorial Analysis

test people in all combinations of the variable

Factorial Design

data is collected in each cell of a table (full factorial analysis); variables should be independent of each other

Assumptions for factorial ANOVA

approximately equal sample sizes in each cell (factorial analysis is NOT robust to unequal sample sizes); residuals are distributed normally (factorial analysis is robust to slight deviations); variances are equal across subgroups; independence of data; all cells have samples

Ways to deal with Assumptions Violations

separate into individual one-way ANOVA’s; transformations; non-parametric methods

Superposition

total is sum of parts; combined effect was the additions of the 2 effects

Interaction Effects

the effects of 2 variables CAN’T be explained by superposition; difference in data that can’t be explained by adding the differences of its parts

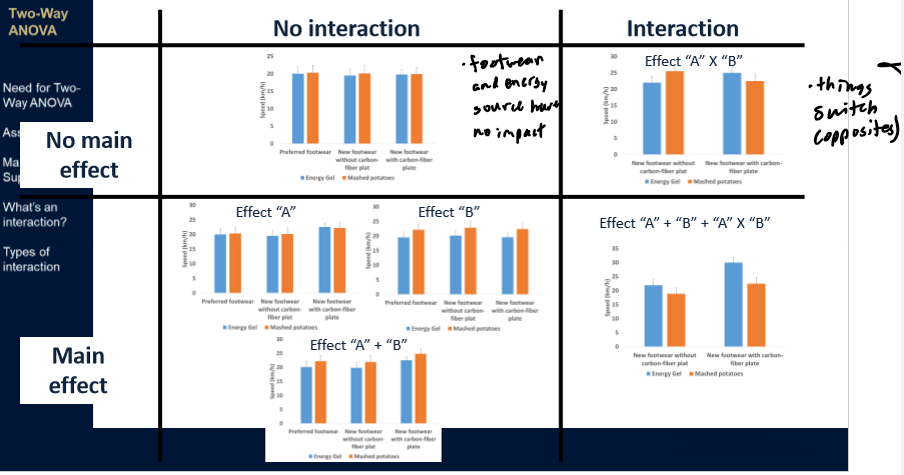
Types of Interaction Effects

1. combination of factors required to observe an effect

2. one factor reverses the effect of another factor

3. one group from A increases the impact of factor “B” or vice versa (synergistic effect)

4. one group from A reduces the impact of factor “B” or vice versa (interference effect) → might expect a certain result but get less than that

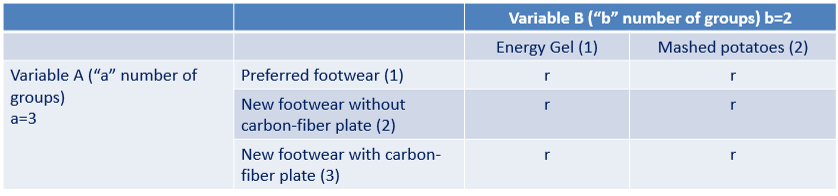
Notation

first subscript: group for variable “A”

second subscript: group for variable “B”

third subscript: trial (from 1 to “r”)

Dot in the Subscript

data was averaged across all values in that subscript

Hypotheses: Main Factors - Variable A

Ho: X1.. = X2.. = … = Xa.. (all group means are equal)

Ho: X1.. - X… = X2.. - X… = … = X1.. - X… = 0

Ha: at least 1 mean within group A deviates from the overall mean

Ha: X1.. - X… =/ 0 or X2.. - X… =/ 0 or Xa.. - X… =/ 0

Hypotheses: Main Factors - Variable B

Ho: X.1. = X.2. = … = X.b. (all group means are equal)

Ho: X.1. - X… = X.2. - X… = … = X.b. - X… = 

Ha: at least 1 mean within group B deviates from the overall mean

Ha: X.1. - X… =/ 0 or X.2. - X… =/ 0 or X.b. - X… =/ 0

Hypothesis Testing: Interaction Effects

absence of superposition

Ho: all sub-group averages are explained by superposition of A and B effects

Ho: Xij. - X… = (Xi.. - X…) + (X.j. - X…) or X11. - X1.. - X.1. + X… = 0 or

X21. - X2.. - X.1. + X… = 0 or X12. - X1.. - X.2. + X… = 0 

Ha: superposition doesn’t fully describe at least one of the group averages

Process for Hypothesis Testing

1. calculate sum of squares for variable A, variable B, interaction (A*B), and error

2. determine df (for A, B, A*B, and error)

3. calculate F-ratio for A, B, and A*B

4. determine critical F-ratio from table (A, B, and A*B)

5. compare calculated to critical F-ratio to evalulate hypothesis

Partitioning Sum of Squares

partitiions it into clever bits

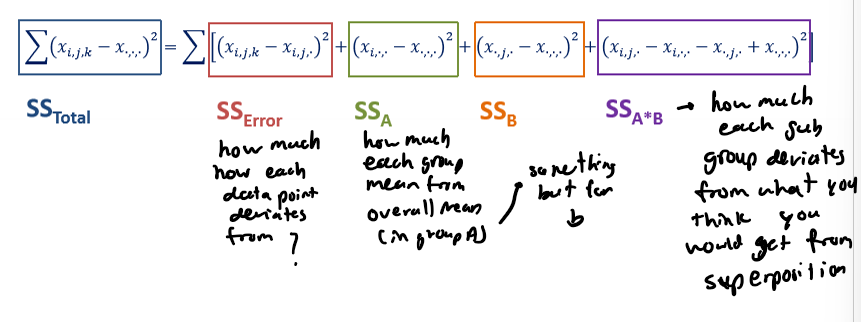
SS(A)

r*b*sum (i = 1 → a) (Xi.. - X…)²; there are r*b trials fro each group within variable A (nj = r*b)

SS(B)

r*a*sum (j=1 to b) (X.j. - X…)²

SS(A*B)

sum (i=1 to a) sum (j=1 to b) * r * (Xij. - Xi.. - X.j. + X…)²; each group combination of (i,j) has r trials in it

SS(error)

sum (i=1 to a) sum (j=1 to b) * (r-1) * sd²ij

sum (i=1 to a) sum (j=1 to b) sum (k=1 to r) * (Xijk - Xij.)²

sdij is the standard deviation across values for the ith group of variable A and jth group of variable B

Degress of Freedom

A = a - 1

B = b - 1

A*B = (a - 1)*(b -1)

Error = N - a*b

Total = N -1 

Mean of Squares

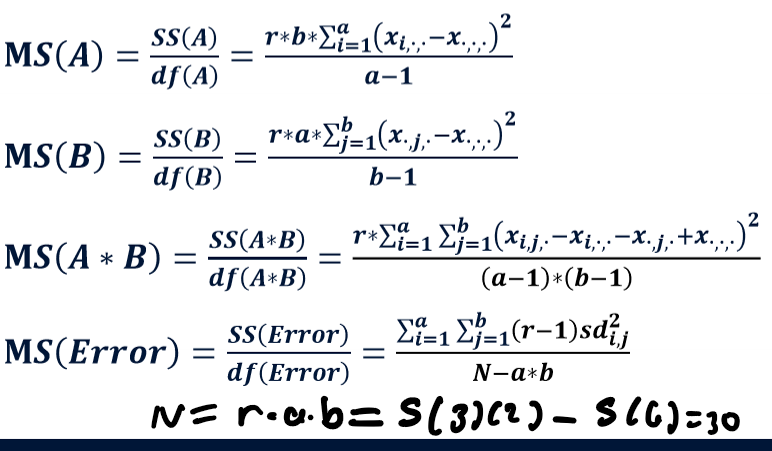
F-ratio

will have 3 of these; all use same error (metric of uncertainity won’t change) and all use same df error

Hypothesis Testing

reject Ho is F > Fcrit