moving charges and magnetism

magnets

inside current carrying conductor, electric field is zero

The electric field inside a current carrying conductor is not zero; it is the electric field outside the conductor that is zero in static conditions.

force on charge outside current carrying element must be zero at rest and constant velocity because electric field is zero

no, force on charge is not zero if it has constant velocity because the magnetic field may exert a force on the moving charge.

tesla and gauss relation

1 T= 10⁴ Gauss

Magnetic field vector or scalar and unit and dimension

Vector

unit Tesla si and Gauss cgs

M¹L⁰T^-2A^-1

small current element IdL is vector or scalar

vector

Biot savarts law

B= u₀/4n IdLsin0/ r²

vector form of biot savarts law

vector form

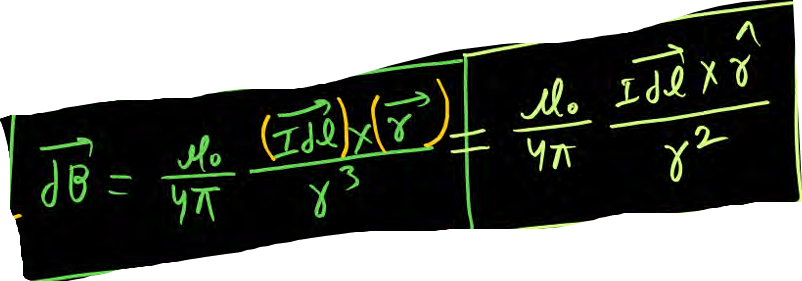
permeability of free space numerical value and dimension

u₀ = 4n x 10^-7

MLT^-2A^-2

permittivity e₀  dimensional formula

M^-1L^-3T⁴A²

Magnetic field characteristics

1. long range field

2. produced by vector component IdL unlike electric field which is produced by a scalar source charge q

3. direction of B is perpendicular to position vector r and current element IdL

4. medium dependent

5. follow superposition theorem

6. follows inverse square law

7. it depends on angle

magnetic field at centre of any circle upto angle theta

B= u₀I/2R (0/2n)

for full circle u₀I/2R

magnetic field at centre for half circle, 1/4th circle and 120 degrees circle

u₀I/ 4R

u₀ I/8R

u₀ I/6R

1. Magnetic field if n number of loops kept together keeping radius contant

2. If same wire is bent into n loops

nB

n²B

magnetic field due to finite straight wire

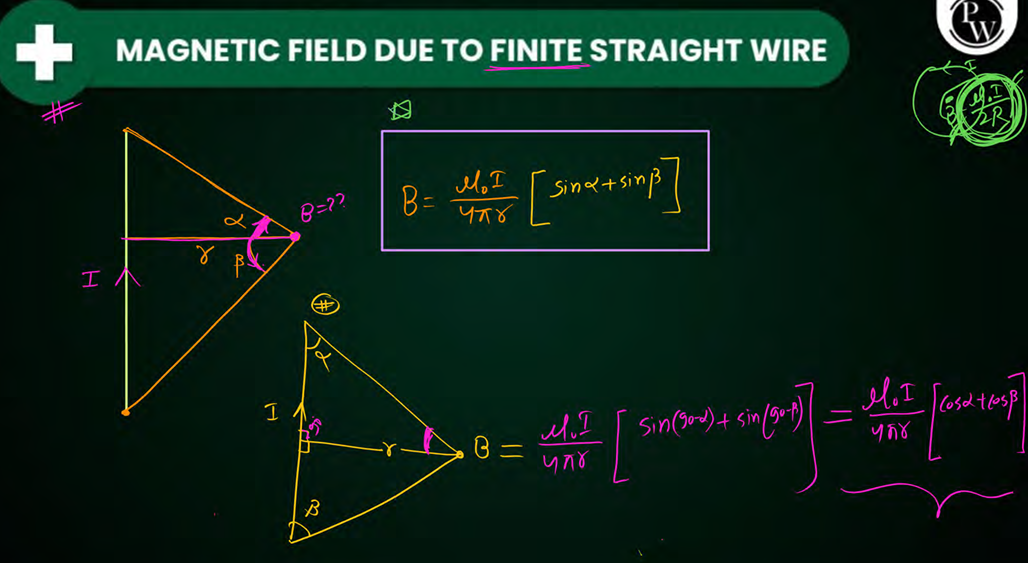
magnetic field due to infinite straight wire

u₀I/2pieR

If concentric circles with radius r, 2r, 4r, 8r, 16r kept with dirn of current opposite in alternate circles. Find field at centre

u₀I/3R

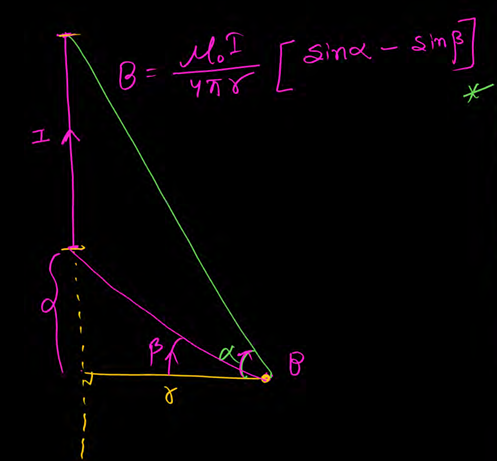
If point taken at lower side of a finite wire then mag field

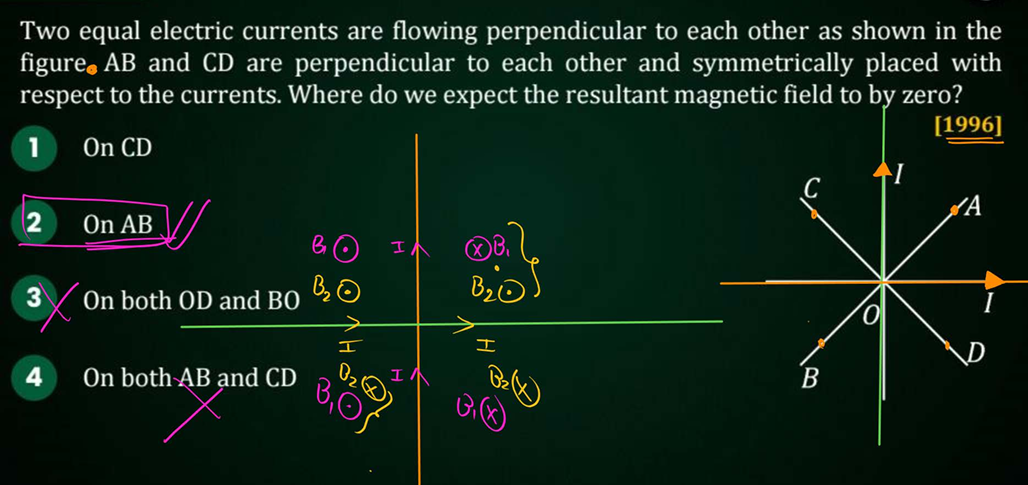
dont panic with so many things just mark the direction of mag field by the two current elements

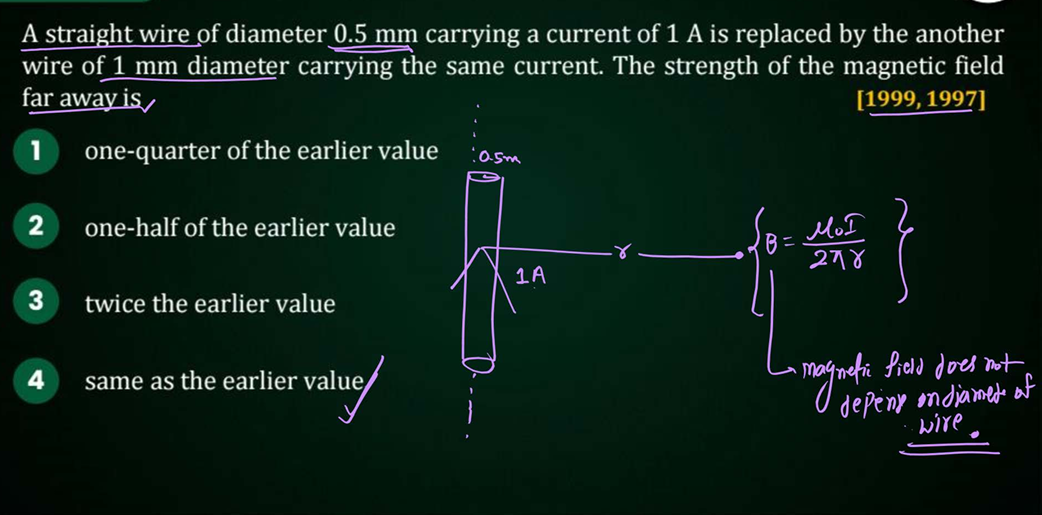
the magnetic field does not depend on diameter of conductor only the distance between conductor and point

Two current components I and nI are in same direction. Find distance from I where field will be zero

x= r/n+1

Two current components I and nI are in different direction. Find distance from I where field will be zero

x= r/n-1

field at centre of current carrying square

2root2 u₀I /  nL

field at centre of current carrying hexagon

root3 u₀I /  nL

three identical current carrying loops placed perpendicular to each other with current I and radius R. find mag field at centre

root3 u₀I/2R

root2 u₀I/2R if two circular loop

dimension dekh lo ya ye dekhlo ki distance d plane se perpendicular hai to root le lenge current i1 i2 ka

field at centre of a square loop where current enters through a and exits through a

Bnet not equal to zero

only zero for current aana jana from different location

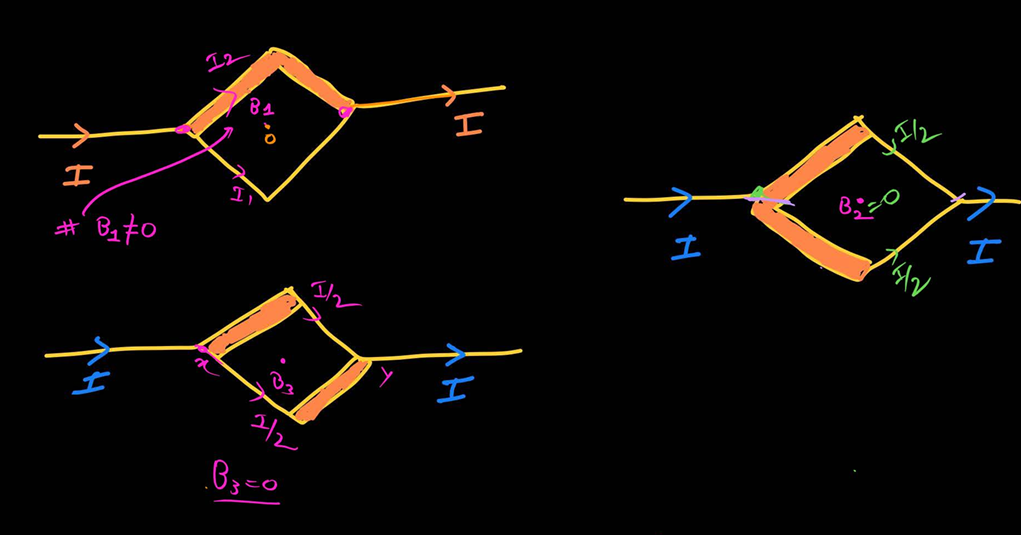
why Bnet not equal to zero in first case

because if we section it into 2 halves along the current then we get two unequal conductors of two width

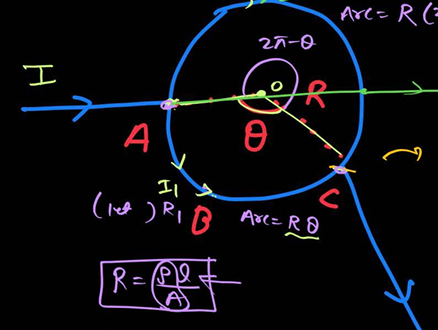
find field due to arc abc

B= u₀i1/2R (0/2n)

where i1 = i(2n-0) / 2n

first mark direction of B1 and B2 then find resultant

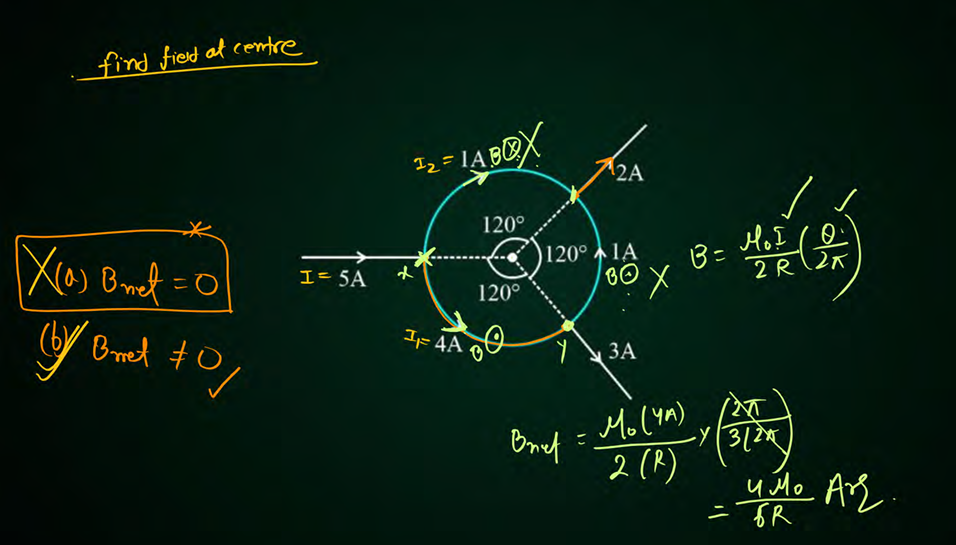
Bnet at centre

Bnet at centre is not zero as 3 arrows present

two current elements with opposite direction will get cancelled

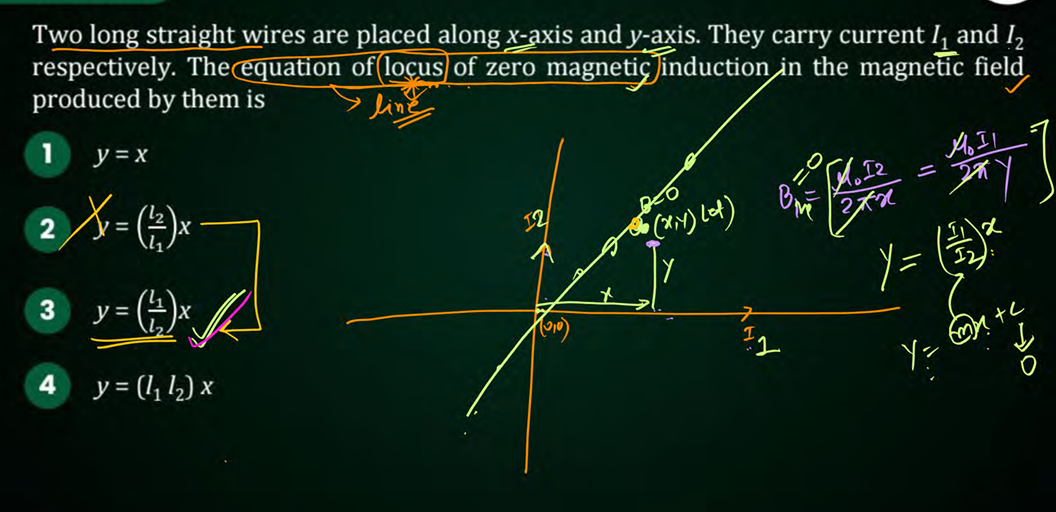
locus nikalne bola hai bss current and distance ka relation nikalo

Magnetic field on axis of circular loop

u₀IR² /2(R²+x²)^3/2

graph for magnetic field on axis of ring

difference b/w gauss law and amperes cicuital law

flux through closed surface= o = E.dA = q_in/ e_o

this is gauss law for 3d objects like sphere cube cylinder

it is not always applicable to calculate elec field only for symmetrical charge distribution

B.dL= u₀ I_in

this is amperes circuital law for loops like ring, square loop not for closed surface

always valid always applicable for symmetric current distribution

magnetic field inside infinite hollow cylindrical wire carrying current i and outside mag field

B inside= 0

B outside= same as infinite wire

magnetic field inside infinite solid cylindrical wire carrying current i and outside mag field

B= u₀Ir/2pieR²

find B.dL for the loops

torque= MB sin0

MB sin0= NIA Bsin0

where N= no of turns

I= current

A= area

B= mag field strength

angle not 30^o because area vector is up and not horizontal with magnetic field

Torque is produced when there is uniform magnetic field and

emf is produced when there is change in magnetic flux so emf not produced

torque and potential energy vector or scalar 

torque vector

potential energy scalar

find time taken by circular loop to turn by angle 90 and become parallel to magnetic field

T= 2n |root i/MB| 

time to turn 360 degrees = T in shm

time for 90 degrees= T/4

so time taken= 2n |root i/MB| /4

angular speed of square coil if it turns by 90 degree and becomes parallel to magnetic field

each arm of square of mass m and length l

root 3iB/m

where i= moment of inertia

B= magnetic field

m= mass of arm

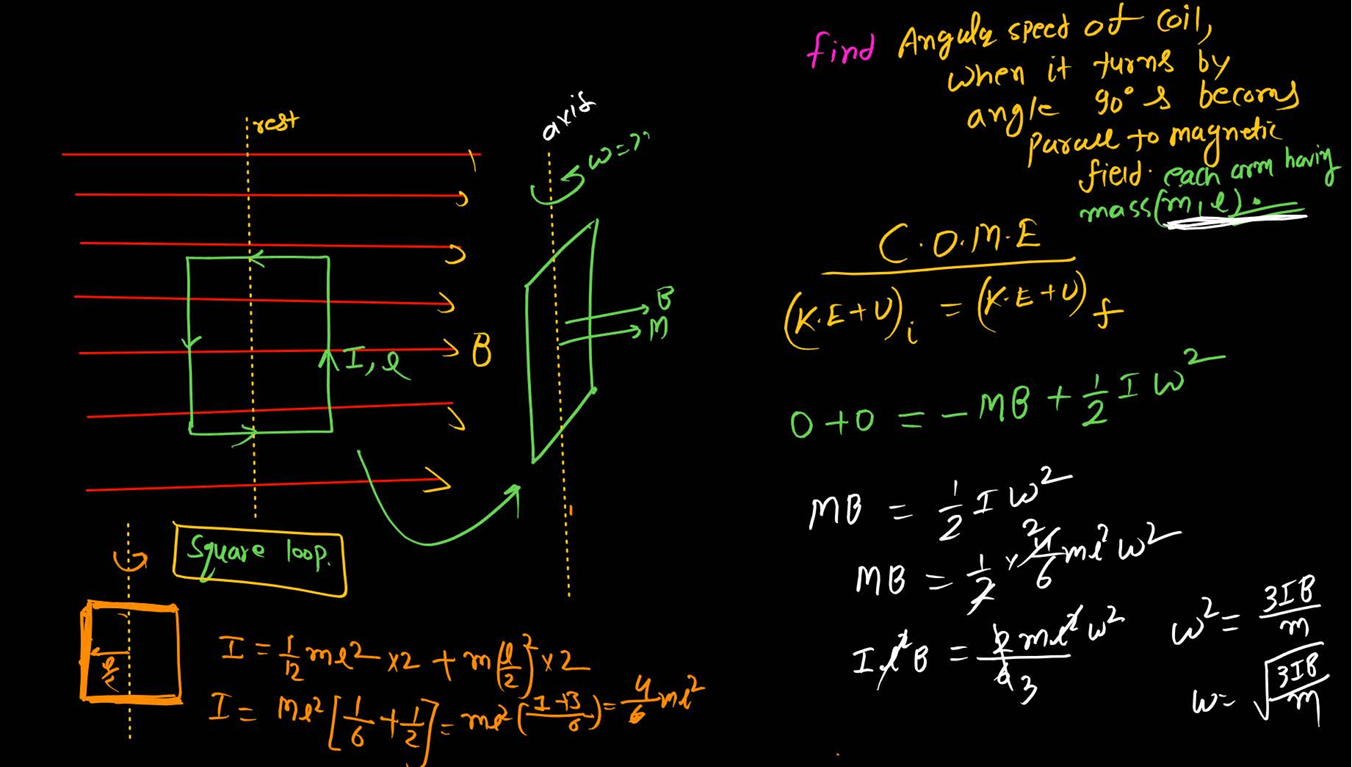
angular speed of circular coil if it turns by 90 degree and becomes parallel to magnetic field

root 4niB/m

i= moment of inertia

m= mass