binomial expansion(y2)

binomial expansion when n is not a positive integer

only works when |x| < 1 as it is an infinite series and will converge to infinity otherwise
works the same if x is bx, but only valid if |bx| < 1 (aka |x| < 1/b)

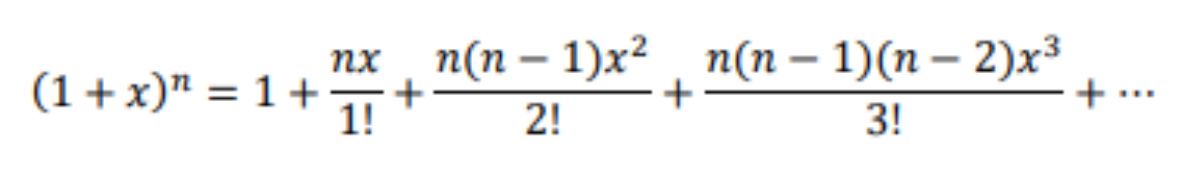
b.e. when n != positive integer and a != 1

the expression must be manipulated into (1 + bx)^n
only valid if |bx/a| < 1 (aka |x| < a/b)

changing (a + bx)^n to (1 + bx)^n

(a + bx)^n = (a(1 + (b/a)x))^n = a^n(1 + (b/a)x)^n
then calculate for (1 + bx/a)^n and multiply the result by a^n

rearranging fractions into binomials (n != posint)

p/(a - bx) rearranges to p(a - bx)^-1 which can be expanded binomially
p can be a single value or can be a binomial itself

partial fractions and binomial expansion

when partial fractions are split, the result is the sum of multiple binomial expressions