Review- Ch 3 Statistics

r

r=Correlation coefficient, the average cross product of z scores

Definition

• Measures the relationship BETWEEN 2 numeric variables

• Strength and association

  • Measures direction(+-) and strength (-1 to 1), not shape

• HOW closely points cluster around the “center” of data

Data

• Univariate data→ mean

• bivariate data→ regression line

• Unitless, so changing the units does nothing

• r must be BETWEEN -1 and 1, with 1 meaning perfect correlation

• Not affected by which variable(x,y) is changing units

• SAME Sign(+-) as the direction of the slope

• STRONGLY affected by extreme values

• If 1 variable has an equattion→ use it

  • (s-x) and (x) have a negative correlation because there is a negative

Math

r= Σ ((x-x̄)/s_x)*(y-ȳ)s_y)) / (n-1)

= Σ( z_x^- z_y) / (n-1)

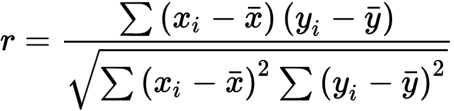
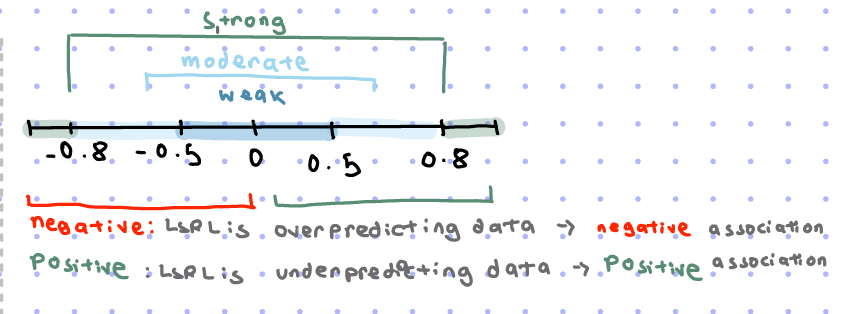
Strength of r

STRENGTH of r, correlation coefficient

Numbers

0 to 0.5 →weak

0.5-0.8 →moderate

0.8 onwards→strong

• A negative: LRSL is overpredicting data→ negative association

• A positive: LRRSL is underpredicting data→ positive association

Least Square Regression Line(LSRL)

• Estimates and predictions, not actual values

• reasonable only WITHIN the domain of the data(Interpolation

• MUST pass through the mean(x̄, ȳ)

• Regression OUTLIERS

  • indicated by a point falling far away from the overall pattern

  • points with relatively large discrepancies BETWEEN the value of the response variable, y, and a predicted value for the response variable,ŷ

Math

LSRL=ŷ =a+bx

• a =y intercept

• b=slope

b=r(s_{y /}s_x)

SSE= Σ(y-ŷ)

• y= Actual

• ŷ=predicted

r²

r^{2=Coefficient of determination}

• Calculates the proportion of the variance(variability) of one variable that is PREDICTED by the other variable

  • “ r² as a 5 of the total variation in Y can be explained by the linear relationship BETWEEN X and Y in the regression line. “

• What % of total data can be explained by the regression line?

• Greater r^2% → Better fit

Math

1-r^{2 ₌} HOW much variability in Y is unaccountable by the regression line.

Describing Scatterplots

SOFA

S:Strength( Strong, Moderate, Weak, variability and Heteroscedasticity)

O: Outliers( in x, y direction, or BOTH)

F: Form(Linear or curved)

A: Association (Positive, negative, or no composition")

• Describing SOFA relationship BETWEEN variables

STEPS

1. Identify the variables, cases, and scale of measure

2. Describe overall shape

3. Describe the trend through the slope

4. describe strength

5. Generalization

6. Note any lurking variables OR causation
   

Heteroscedasticity

• Unequal variation in the plot

• “Fanning left/right”

• Doesn’t cause bias in the coefficient estimates, but make them less precise.

  • Lower precision increases the likelihood that the coefficient estimates are further from the correct population value.

• tends to produce p-values that are smaller than they should be

Scatterplots

Graph

• change can be seen in frequency bar charts

• clusters→ modes(peaks, which can also show bimodal)

• Scatterplots are only for bivariate data

Z score

• Standardised Z

• x, y values will be based on their +-, meaning their points location on the 4 quadrants of the coordinate plane, the origin (0,0) being the intersection

Regression

• HOW 2 numerical variables AFFECT each other

• (x, y) are not interchangeable

• “Casual” affect, but NOT causation

• Positive when independent and dependent variables are both increasing or decreasing together

• Negative when independent and dependent variables are going opposite ways(ie. one is increasing the other is decreasing)

Mean

• the regression to the mean: in ANY elliptical cloud of points whenever the correlation, r, is not perfect

  • A line fitting through this elliptical cloud has a slope of 1

Interpolation

Predicting data value within the dataset

Extrapolation

Predicting data value Outside the dataset

Slope interpretation

“for every 1 unit increase in the explanatory variable, x, there is a slope increase/decrease in the response variable, y.

SSE

The sum of square residual error

Residuals

*distance measurement

• The net sum of residual and mean=0

• The DIFFERENCE between an observed Y value and its predicted value from the regression line

  • Decreases when the regression line fits MORE data

Math

Residual= Y-ŷ

Positive output: linear model UNDERestimated the actual response variable

Negative output: linear model OVERestimated the actual response variable

Residual Plots

• Scatter plot of regression residuals AGAINST the predicted y values

• a “barometer” for HOW well the regression lines fit the data

• curvature →sign of curvature in the original plot, meaning the original was a nonlinear regression

rules for regression

1. The sum of residuals=0

2. horizontal line: mean of residuals=0

3. Residual Scattered=better fit for data

4. Residual have pattern/curve= Not an appropriate line

Missed features in Scatterplots

• These points will change the measurement

• Influential points

• High leverage points

• outliers

• lurking variables

Influential points

• examples: Outliers, high-leverage

• removal of points→sharply CHANGE the regression line

• High leverage

  • x values are far from x̄

  • line up with pattern: doesn’t influence equation, strengthens correlation, r, and determination, r²

  • Not line up with pattern: dramatically CHANGES the equation, an influential point

• Outliers

  • may cause r² and S to CHANGE

• lurking variables

  • Correlation ≠ causation

Slope Changing Transformations

• Line of fit to a scatterplot should be considered for a plot with curvature → adjust the plot using transformations

• Nonlinear transformations change the shape of the graph, linear won’t

  • in terms of slope and correlation,r

• ONLY required if a linear model/scatterplot has curvature

  • use log(ln) or log(log) depending on the plot

  • exponential and power

Exponential transformation

y=ab^x

New equation: log y=log a +x log b

• generally used for growth in population

Power Transformation

y= ax^b

New Equation: log y-log a+b log x

• need to log the variable → final answer is 10^ans

• generally used for relationships BETWEEN height and weight

Common Transformations

Power Transformations

Calculator interpretation

Variable =x, explanatory variable

coefficient constant=y intercept, a

coefficient with variable= slope, b

Error SS=SSE

Residual:SSE