Math - Chapter 2.1 - 2.3

Simplify the following:

a) (3x² + 4x - 10) + (4x² - 10x - 2)

b) (2x² - 5x + 3) - (x² - 2x - 2)

c) (2x² + 6x - 1) - (4x² - 2x - 5) + (3x² - 5x - 1)

a) 7x² - 6x - 12

b) x² - 3x + 5

c) x² + 3x + 3

Determine whether the following functions are equivalent

f(x) = (2x² - 7x - 2) - (3x + 7)

g(x) = (x² + 12) + (x² + 4x - 17)

f(x) ≠ g(x)

Simplify:

a) (3x² - 7x + 5) + (x² - x + 3)

b) (x² - 6x + 1) - (-x² - 6x + 5)

c) (2x² - 4x + 3) - (x² - 3x + 2) + (x² - 1)

a) 4x² - 8x + 8

b) 2x² - 4

c) 2x² - x

Show that f(x) and g(x) are equivalent by simplifying each:

f(x) = (2x - 1) - (3-4x) + (x + 2)

g(x) = (-x + 6) + (6x - 9) - (-2x - 1)

• f(x) = 7x - 2

• g(x) = 7x - 2)

• f(x) = g(x)

Kosuke wrote a mathematics contest consisting of 25 multiple-choice questions. The scoring system gave 6 points for a correct answer, 2 points for not answering a question and 1 point for an incorrect answer. Kosuke got x correct answers and left y questions unanswered.

a) Write an expression for the number of questions he answered incorrectly.

b) Write an expression in simplified form, for Kosuke’s score

c) Use the equation you wrote in parts a) and b) to determine Kosuke’s score if he answered 13 correctly and 7 incorrectly

a) 25 - x - y

b) 5x + y + 25

c) 95

The two equal sides of an isosceles triangle each have a length of 2x + 3y - 1. The perimeter of the triangle is 7x + 9y. Determine the length of the third side.

• 3x + 3y + 2

Tino owns a small company that produces and sells cell phone cases. The revenue and cost functions for Tino’s company are shown below, where x represents the selling price in dollars.

Revenue: R(x) = -50x² + 2500x

Cost; C(x) = 150x + 9500

a) Write the simplified form of the profit function

b) What profit will the company make if it sells the cases for $12 each

a) P(x) = -50x² + 2350 - 9500

b) $11 500

What are the different types of factoring

• common

• grouping

• Trinomial a = 1

• Trinomial a ≠ 1

• Perfect square trinomial (PST)

• Difference of Squares

What is an example of common factoring

• 6x² + 9x = 3x(2x + 3)

What is an example of grouping

• x² + 5x + 2x + 10 = (x+5)(x+2)

What is an example of trinomial a = 1 factoring

• x² + 7x + 12 = (x + 3)(x + 4)

What is an example of Trinomial a ≠ 1 factoring

• 2x² + 7x + 3 = (2x + 1)(x + 3)

What is an example of perfect square trinomial (PST) factoring

• x² + 6x + 9 = (x + 3)²

What is an example of differences of squares factoring

• x² - 16 = (x + 4)(x - 4)

Factor the following and identify the type of factoring you used:

a) 2x² - 10x

b) x² - 9x + 18

c) x³ + 3x² + 2x + 6

d) 4x² + 2x - 6

e) x² - 64

f) x² - 10x + 25

g) 18x² - 50

h) 10x² - x - 3

a) 2x(x - 5) → common factoring

b) (x - 6)(x - 3) → Trinomial a = 1

c) (x² + 2)(x + 3) →Grouping

d) 2(2x - 3)(x - 1) → Common factor and Trinomial a ≠ 1

e) (x - 8)(x + 8) →Differences of squares

f) (x - 5)² → Perfect square trinomial (PST)

g) 2(3x - 5)(3x + 5) → Common factor and differences of squares

h) (5x - 3)(2x + 1) →Trinomial a ≠ 1

Factor and name type of factoring used:

a) x² - 6x - 27

b) 25x² - 49

c) 4x² + 20x + 25

d) 6x² - x - 2

a) (x + 3)(x - 9) →Trinomial a = 1

b) (5x - 7)(5x + 7) →Differences of squares

c) (2x + 5)² → Perfect square trinomial

d) (2x + 1)(3x - 2) →Trinomial a ≠ 1

Factor and list type of factoring used:

a) x² - 3x - 28

b) 36x² - 25

c) 9x² - 42x + 49

d) 2x² - 7x - 15

a) (x - 7)( x + 4) →Trinomial a = 1

b) (6x - 5)(6x + 5) → Differences of squares

c) (3x - 7)² → Perfect square trinomial (PST)

d) (2x + 3)(x - 5) →Trinomial a ≠ 1

Factor and list type of factoring used:

a) 5x(2 - x) + 4x(2x - 5) - (3x - 4)

b) 4t(t² + 4t + 2) - 2t(3t² - 6t + 17)

a) (x - 4) (3x - 1) →Grouping and Trinomial a ≠ 1

b) -2t(t - 13)(t - 1) → Common factor and Trinomial a = 1

Factor and list type of factoring used:

a) x² - 5x - 14

b) x² + 4xy - 5y²

c) 6m² - 90m + 324

d) 2y² + 5y - 7

e) 8a² - 2ab - 21b²

f) 16x² + 76x + 90

a) (x + 2)(x - 7) →Trinomial a = 1

b) (x + 5y)(x - y) →Trinomial a = 1

c) 6(m - 6)(m - 9) → Common factor and trinomial a = 1

d) (2y + 7)(y - 1) →Trinomial a ≠ 1

e) (4a - 7b)(2a + 3b) → Trinomial a ≠ 1

f) 2(2x + 5)(4x + 9) → Common factor and trinomial ≠ 1

Factor and list the type of factoring:

a) x² - 9

b) 4n² - 49

c) x⁸ - 1

d) 9(y - 1)² - 25

e) 3x² - 27(2 - x)²

f) -p²q² + 81

a) (x - 3)(x + 3) →Differences of squares

b) (2n - 7)(2n + 7) →Differences of squares

c) (x - 1)(x + 1)(x² + 1)(x⁴ + 1) →Differences of squares

d) (3y + 8)(3y - 2) → trinomial a ≠ 1

e) -12(2x - 3)(x - 3) →common and Trinomial a ≠ 1

f) -(pq - 9)(pq + 9) → Differences of squares

Factor and list the types of factoring used:

a) ax + ay + bx + by

b) x³ + x² - x - 1

c) 1 - x² + 6x - 9

d) a² - b² + 25 + 10a

a) (a + b)(x + y) → Grouping

b) (x - 1)(x + 1)² → Grouping and difference of squares

c) (x - 2)(4 - x) →Trinomial a ≠ 1

d) (a + 5 + b)(a + 5 - b) → Perfect square trinomial (PST) and difference of squares

Factor:

a) 2x(x - 3) + 7(3 - x)

b) x³ - x² - 4x + 4

c) y² - 49 + 14x - x²

a) (2x - 7)(x - 3)

b) (x - 2)(x + 2)(x - 1)

c) (y - x)(y + x) + 7(2x - 7) = (y - x + 7)(y + x - 7)

Sedna has designed a fishpond in the shape of a right triangle with two sides of length a and b and hypotenuse of length c.

a) Write an expression in factored form for a²

b) The hypotenuse is 3m longer than b, and the sum of the lengths of hypotenuse and b is 11m. What are the lengths of the sides of the pond

a) a² = (c - b)(c + b)

b) a = √33m b = 4m c = 7m

Expand and simplify the following:

a) 2(x² - 3x + 2) - 3(2x² - 3)

b) 2(x - 4)² - 2x(3x - 2)

a) -4x² - 6x + 13

b) -4x² - 12x + 32

Determine a simplified function that represents the volume of the given box

h = x + 3

l = x + 1

w = x + 2

• V(x) = x³ + 6x² + 11x + 6

A rectangle is twice as long as it is wide. Write an expression for the change in area if the length of the rectangle is increased by 1 and the width is decreased by 1.

• The change in the area (Anew - Aog) is

  • -w - 1

Expand and simplify

a) 4(n - 4)(3 + n) - 3(n - 5)(n + 8)

b) 3(2x - 1)² - 5(4x + 1)²

c) 2(3a + 4)(a - 6) - (3 - a)² + 4(5 - a)

a) n² - 13n + 72

b) -68x² - 53x - 2

c) 5a² - 26a - 37

A cylinder with a top and bottom has a radius of 2x + 1 and height of 2x - 1. Write an expression for its:

a) Surface area, where SA = 2πr² + 2πrh

b) Volume, where V = πr²h

a) 16πx² + 8πx

b) 8πx³ + 4πx² - 2πx - π

Expand and simplify:

2(x + 1)² - 3(2x - 1)(3x - 5)

• -16x² + 43x - 13

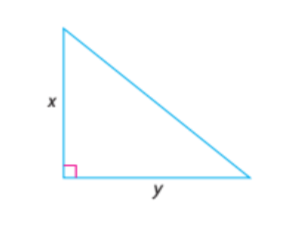
The two sides of a right triangle have lengths x and y. Represent the change in the triangle’s area if the length of one side is doubled and the length of the other side is halved.

0