T-tests

What is a t-test

Used to compare two means (or medians) 

Not good for repeated comparisons (use ANOVA) 

ex: performing 3 t-tests for same data 

What are the types of t-tests

1. one sample t-test

2. student’s (unpaired) t-test

3. paired t-test

Describe one-sample t-test

Compares a sample mean to a given population mean 

• Requires normally distributed population and population mean is known 

  • Population doesn’t need to be the overall population, can be a subset within the population 

  • Sample SD won’t have a normal distribution because it is NOT a population SD 

• Still need two means (one is yours (sample) and the other is the population) 

  • One sample is compared to a population 

  • Is there a significant difference between the sample and population? 

• Can be one-tailed OR two-tailed 

• NEED:  

  • Sample mean, sample SD, population mean, sample size (n), table of critical t-values or simple computer statistical program 

• Ex: The six students get scores of 67, 89, 77, 68, 83, 98. Can the professor be at least 95% certain that the mean score for the class on the test would be at least 70? 

  • Sample = the 6 students 

  • Population = the class 

CLASS:

ONLY ONE THAT SAMPLE IS COMPARED TO THE POPULATION

• compared to larger population/larger group/subset of larger group

• sample mean vs population mean

Describe a student’s t-test

Compares two sample means. Therefore is a TWO sample t-test 

• Two sample groups 

• Is one sample mean significantly different from the other? 

• Requires two normally distributed but independent populations, population mean is unknown 

  • Is there a difference between control group and experimental group 

• Needs: 

  • Two sample, means, two sample SD, both sample sizes (n), & table of critical t-values or stats program 

• Ex: An experiment is conducted to determine whether a new gasoline additive can increase the gas mileage of SUVs. SUVs were chosen randomly and put into either the “additive” group or “no additive” group. Gas mileage was determined for the vehicles in each group 

  • Sample 1= Additive group 

  • Sample 2= no additive group 

CLASS:
Comparing 2 samples to each other

• looking at the same dependent variable in both samples (ONLY 2 SAMPLES)

Describe a paired t-test

Compares one set of measurements with a second set of measurements from the SAME sample (“goes together”) 

• Requires a set of paired observations from a normal population 

• More powerful than an unpaired because most extraneous values will be the same across both treatment conditions 

  • Limited amount of growth or change in the extreme values (example: if you have a 90 can only get 10 more points on a test) 

• Compare the “before” and “after” of the same sample 

  • Two sample groups 

• Ex: Does a week of tutoring help a group of students improve their scores on a calculus test? 

  • Sample 1= Before tutoring 

  • Sample 2= After tutoring  

CLASS:
ONE SAMPLE @ 2 DIFFERENT POINTS IN TIME

• before and after activity/research experiment

• SAME SAMPLE at 2 different points in time

  • If there is 3 points in time (it is repeated measures ANOVA)

What are the 4 assumptions made when performing t-tests

1. Normal/gaussian distribution 

2. Randomly sampled 

3. Equal variances 

   • Large sample with larger variances, test is less powerful 

     • Concern if null is not rejected 

   • If smaller sample has large variance, type 1 error increases 

     • Concern if null is rejected 

   • t-test with unequal variances can be modified to compensate (Welch corrected) 

4. Data measured on interval or ratio scale 

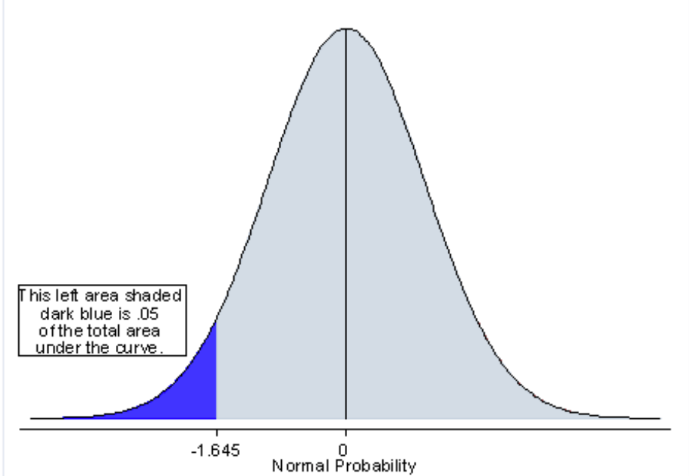
What is a one-tailed test

One-tailed = a directional hypothesis 

• Expect to see one group to shift in a particular direction 

• Put 0.05 on one side of the curve 

• More likely to make type 1 error 

  • Because don’t travel as much from the start to 0.5 end 

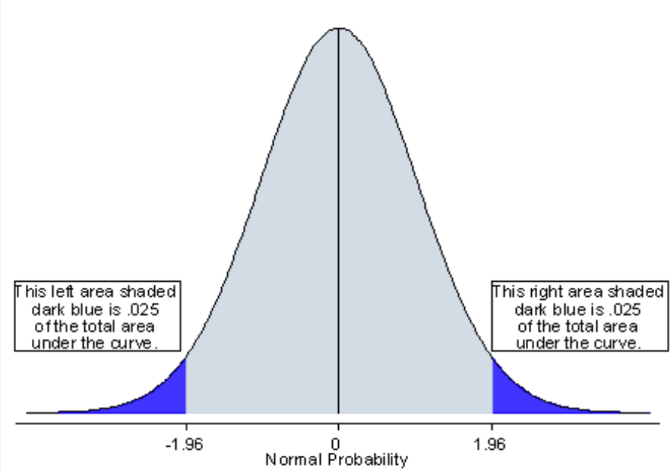
What is a two-tailed test

Two-tailed = more conservative than one-tailed because it takes a more extreme stat to reject null hypothesis 

• Splits the 0.5 on both sides of the curve 

  • 0.25 on each end of the curve 

• Bigger difference between 0 (start point) to the 0.25 region 

What are some scenarios you would use a particular “tailed” test

One tailed test = must be specific reason why you would only expect a difference in one direction 

Two tailed test = if there’s a possibility that the difference could be in either direction, even if hypothesis is directional  

How do you interpret a p value in context to a research question

Alpha = 0.05 

If P is less than 0.05, then results ARE significant 

Null hypothesis rejected 

If P is greater than 0.05, then results are NOT significant 

Because too great of a chance to have a false positive 

Null hypothesis accepted 

Given a research question or scenario, pick the appropriate statistical test to analyze the data

think of examples from class

one-way = 1 sample in the study that will be compared to the population

student’s = 2 different samples (control and experimental) that are compared to each other

paired = 1 sample that is measured twice. Ex: the weight of a group “before” and “after” testing Ozempic