Chapter 2: Syntax and Semantics of Propositional Logic

Sentence letters are…

P, Q, R, P₁, Q₁, R₁, P₂, Q₂, R₂ and so on

Sentences of 𝐿₁ are…

All sentence letters,

If Φ and Ψ are, then ¬Φ, (Φ ∧ Ψ), (Φ ∨ Ψ), (Φ → Ψ) and (Φ ↔ Ψ) are too,

Nothing else.

Bracketing convention 1

The outer brackets may be omitted from a sentence that is not part of another sentence.

Bracketing convention 2

The inner set of brackets may be omitted from a sentence of the form ((φ∧ψ) ∧χ) and analgously for ∨.

Bracketing convention 3

Suppose ⬦∈{∧, ∨}and ⚬∈{→, ↔}. Then if (φ⚬(ψ⬦χ)) or ((φ⬦ψ)⚬χ) occurs as part of the sentence that is to be abbreviated, the inner set of brackets may be omitted.

An 𝐿₁-structure is…

an assignment of exactly one truth-value (T or F) to every sentence letter of 𝐿₁.

Truth in an 𝐿₁-structure.

Truth tables for each logical connective

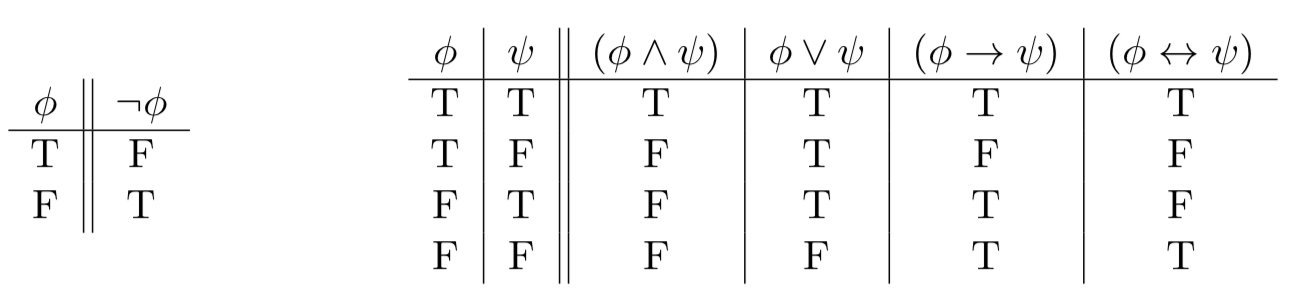
A sentence Φ of 𝐿₁ is logically true iff…

Φ is true in all 𝐿₁-structures.

Any sentence Φ of 𝐿₁ is a contradiction iff…

Φ is not true in any 𝐿₁-structure.

A sentence Φ and a sentence Ψ are logically equivalent iff…

Φ and Ψ are true in exactly the same 𝐿₁-structures.

Logical Validity

Let Γ be a set of sentences of 𝐿₁ and Φ a sentence of 𝐿₁. The argument with all sentences in Γ as premisses and Φ as conclusion is valid if and only if there is no 𝐿₁-structure in which all sentences in Γ are true and Φ is false.

An 𝐿₁-structure is a counterexample…

to the argument with Γ as the set of premisses and Φ as conclusion if and only if |Ψ|A = T for all Ψ ∈ Γ and |Φ|A = F. Therefore, an argument in 𝐿₁ is valid if and only if it does not have a counterexample.

A set Γ of 𝐿₁-structures is semantically consistent iff…

there is an 𝐿₁-structure A such that |Φ|A = T for all sentences Φ of Γ.