Week 7-9 - Uncertainty Handling

Week 7-9 - Uncertainty Handling

This arises when the available information is incomplete, unreliable, or conflicting.

Uncertainty

Examples of Uncertainty:

• A medical expert system diagnosing a disease might not have full patient data.

• A network security system detecting an attack may only have partial evidence.

Uncertainty arises when the available information is ?

• incomplete

• unreliable

• conflicting

TRUE OR FALSE

It is common in expert systems where reasoning is based on probabilities rather than absolute truths.

TRUE

This deals with imprecise or vague information, often found in linguistic terms.

Fuzziness

Examples of Fuzziness:

• A thermostat set to "warm" instead of a precise temperature.

• A cybersecurity rule stating "high network traffic may indicate an attack."

Fuzziness deals with imprecise or vague information, often found in?

linguistic terms

TRUE OR FALSE

Unlike uncertainty, which is about the lack of knowledge, fuzziness concerns gradual changes rather than strict classifications.

TRUE

ENUMERATE: Techniques for Handling Uncertainty

• Probability Theory (Bayesian Networks)

• Dempster-Shafer Theory

• Certainty Factors (CF)

A technique for handling uncertainty that uses probabilities to model uncertain events.

Probability Theory (Bayesian Networks)

Example: In medical diagnosis, a Bayesian network can calculate the probability of a disease given symptoms.

A technique for handling uncertainty that extends probability theory by allowing belief representation with unknown probabilities.

Dempster-Shafer Theory

Example: An intrusion detection system assigns belief to different threat sources.

A technique for handling uncertainty used in MYCIN (a medical expert system) to handle expert knowledge uncertainty.

Certainty Factors

In certainty factors, each rule has a certainty factor ranging from ?

-1 (false) to +1 (true).

Example: "If fever → flu (CF = 0.8)" means the system is 80% confident.

ENUMERATE: Techniques for Handling Fuzziness

• Fuzzy Logic

• Membership Functions

• Fuzzy Inference Systems (FIS)

A technique for handling fuzziness that uses degrees of truth rather than binary (true/false) logic.

Fuzzy Logic

Example: In an expert system for air conditioning, instead of "hot" or "cold," fuzzy logic allows "somewhat hot" or "moderately cold."

A technique for handling fuzziness that define how input values belong to fuzzy sets.

Membership Functions

Example: "Tall people" can have a membership function where 5'8" is 0.5 tall, and 6'5" is 1.0 tall.

A technique for handling fuzziness that uses fuzzy rules (IF-THEN statements) to infer conclusions.

Fuzzy Inference System (FIS)

Example: A cybersecurity expert system might use rules like:

"IF network traffic is high AND suspicious activity is moderate, THEN threat level is medium."

Differences Between Uncertainty and Fuzziness

Application of understanding Uncertainty and Fuzziness in Expert Systems

• Medical Diagnosis (Uncertainty in patient symptoms)

• Network Security (Fuzzy rules for intrusion detection)

• Weather Forecasting (Probability-based predictions)

• Industrial Automation (Fuzzy control for machine adjustments)

ENUMERATES: Types of Uncertainty in AI

• Aleatoric Aleatoric Uncertainty (Statistical Uncertainty)

• Epistemic Uncertainty (Model Uncertainty)

• Ontological Uncertainty (Conceptual Uncertainty)

A type of uncertainty in AI that is due to inherent randomness in data.

Aleatoric Uncertainty (Statistical Uncertainty)

Example: A self-driving car’s vision system struggles with foggy conditions.

A type of uncertainty in AI that is due to lack of knowledge or insufficient data.

Epistemic Uncertainty (Model Uncertainty)

Example: A medical AI model misclassifies a rare disease due to a lack of training examples.

A type of uncertainty in AI that is due to poorly defined or evolving concepts.

Ontological Uncertainty (Conceptual Uncertainty)

Example: Cybersecurity AI detecting "zero-day" attacks with no prior knowledge.

Solution to Aleatoric Uncertainty (Statistical Uncertainty)

Probabilistic models like Gaussian Processes

Solution to Epistemic Uncertainty (Model Uncertainty)

• Bayesian neural networks (BNNs)

• Monte Carlo Dropout

Solution to Ontological Uncertainty (Conceptual Uncertainty)

• Continual learning

• Fuzzy logic

It deals with gradual transitions and linguistic vagueness instead of binary classification.

Fuzziness

Unlike uncertainty, which is about unknown information, fuzziness allows?

soft decision boundaries

Example:

Instead of classifying email spam as "spam" or "not spam", fuzzy logic allows classification like:

• "Highly likely spam (0.9)", "Somewhat spam (0.5)", "Not spam (0.1)"

Uses membership functions to assign degrees of truth.

Implements fuzzy rules (IF-THEN statements).

Useful in control systems, recommendation systems, and AI-driven automation.

Fuzzy Logic in AI

ENUMERATES: Techniques for Handling Uncertainty in AI and ML

• Probabilistic Models (Bayesian Inference)

• Monte Carlo Dropout (Uncertainty Estimation in Deep Learning)

• Fuzzy Logic for Handling Fuzziness

• Dempster-Shafer Theory (Belief Theory)

• Gaussian Processes (GPs) for Uncertainty Estimation

A techniques for handling uncertainty in AI and ML that uses probability distributions to estimate uncertainty.

Probabilistic Models (Bayesian Inference)

Example: Bayesian Neural Networks (BNNs) estimate confidence in predictions.

A techniques for handling uncertainty in AI and ML where dropout layers randomly disable neurons during training and inference.

It helps quantify uncertainty in neural network predictions.

Monte Carlo Dropout (Uncertainty Estimation in Deep Learning)

Example: AI in medical imaging can predict lung disease probability with confidence scores.

It is the uncertainty estimation in deep learning.

Monte Carlo Dropout

In Monte Carlo Dropout, these randomly disable neurons during training and inference.

dropout layers

A techniques for handling uncertainty in AI and ML that maps continuous input variables to fuzzy categories.

Fuzzy Logic for Handling Fuzziness

Example: AI-based climate control system adjusting temperature based on "warm," "hot," "cool" instead of precise degrees.

A techniques for handling uncertainty in AI and ML that assigns degrees of belief rather than precise probabilities.

Dempster-Shafer Theory (Belief Theory)

Example: AI in network security detects potential cyber threats with confidence intervals.

A techniques for handling uncertainty in AI and ML that is used in reinforcement learning and robotics. It predicts outputs along with uncertainty estimates.

Gaussian Processes (GPs) for Uncertainty Estimation

Example: AI-driven self-driving cars navigating uncertain road conditions.

Applications of Uncertainty and Fuzziness in AI

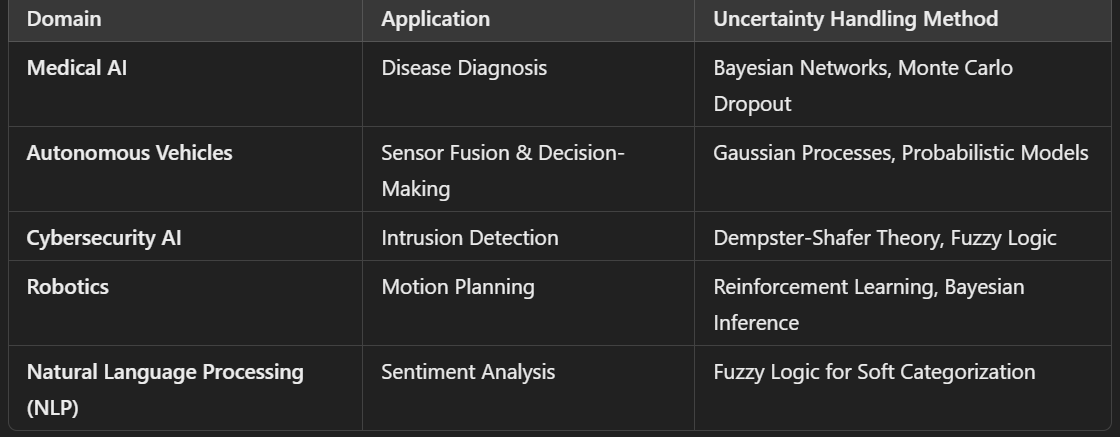
Scenario: AI-Based Intrusion Detection System (IDS)

• A cybersecurity AI detects threats based on network traffic patterns.

• Challenges:

  • Attack data is incomplete.

What is the uncertainty that is displayed?

Epistemic Uncertainty

Scenario: AI-Based Intrusion Detection System (IDS)

• A cybersecurity AI detects threats based on network traffic patterns.

• Challenges:

  • Traffic behavior is random

What is the uncertainty that is displayed?

Aleatoric Uncertainty

Scenario: AI-Based Intrusion Detection System (IDS)

• A cybersecurity AI detects threats based on network traffic patterns.

• Challenges:

  • Some attacks use new patterns

What is the uncertainty that is displayed?

Ontological Uncertainty

Cybersecurity AIScenario: AI-Based Intrusion Detection System (IDS)

• A cybersecurity AI detects threats based on network traffic patterns.

• Challenges:

  • Attack data is incomplete (Epistemic Uncertainty).

  • Traffic behavior is random (Aleatoric Uncertainty).

  • Some attacks use new patterns (Ontological Uncertainty).

Provide Solutions

Solution:

1. Probabilistic Model (Bayesian Networks)

   • Predicts attack likelihood based on observed patterns.

2. Fuzzy Logic

   • Classifies threats as low, medium, or high risk instead of binary detection.

3. Monte Carlo Dropout

   • Estimates uncertainty in deep learning-based anomaly detection.

Deep learning models are often used for complex decision-making, but real-world data is inherently?

uncertain and fuzzy

TRUE OR FALSE

Handling uncertainty and fuzziness in deep learning is crucial for improving model reliability, interpretability, and robustness.

TRUE

ENUMERATE: Types of Uncertainty in Deep Learning

• Aleatoric Uncertainty (Data Uncertainty)

• Epistemic Uncertainty (Model Uncertainty)

• Ontological Uncertainty (Conceptual Uncertainty)

A type of Uncertainty in Deep Learning that arises from random noise in data.

Aleatoric Uncertainty (Data Uncertainty)

• Example: A self-driving car's camera struggles with foggy weather, leading to uncertain object detection.

• Solution: Model learns to predict uncertainty alongside predictions (e.g., heteroscedastic models).

A type of Uncertainty in Deep Learning due to lack of knowledge or insufficient data.

Epistemic Uncertainty (Model Uncertainty)

• Example: A medical AI misclassifies rare diseases due to limited training data.

• Solution: Bayesian Neural Networks (BNNs), Monte Carlo Dropout (MC Dropout).

A type of Uncertainty in Deep Learning due to uncertainty in problem definition or evolving concepts.

Ontological Uncertainty (Conceptual Uncertainty)

• Example: A cybersecurity AI struggles to detect zero-day attacks (never seen before).

• Solution: Continual learning, fuzzy logic-based reasoning.

ENUMERATE: Techniques for Handling Uncertainty in Deep Learning

• Bayesian Deep Learning

• Monte Carlo Dropout (MC Dropout)

• Gaussian Processes in Deep Learning

This estimate uncertainty in weights instead of fixed values.

Bayesian Neural Networks (BNNs)

• Example: AI predicting medical diagnoses also provides a confidence level for each prediction.

Using this during inference estimates uncertainty in deep learning predictions.

Monte Carlo Dropout

Introduces stochasticity by keeping dropout active during inference.

Monte Carlo Dropout (MC Dropout)

• Example: AI for pneumonia detection outputs a probability score with uncertainty range.

Helps quantify uncertainty in classification and regression tasks.

Monte Carlo Dropout (MC Dropout)

• Example: AI for pneumonia detection outputs a probability score with uncertainty range.

This provide a distribution over predictions, rather than single-point estimates.

Gaussian Processes in Deep Learning

• Example: A robot using a deep RL model for navigation estimates uncertainty to avoid risky movements.

Used in reinforcement learning (RL), robotics, and decision-making.

Gaussian Processes in Deep Learning

• Example: A robot using a deep RL model for navigation estimates uncertainty to avoid risky movements.

Deep learning models are typically ______, but real-world problems involve gradual changes rather than strict categories.

crisp classifiers

Deep learning models are typically crisp classifiers, but real-world problems involve ________ rather than strict categories.

gradual changes

This allows deep learning models to handle gradual transitions and imprecise categories.

Fuzzy Logic

• Example: AI classifies movie reviews as "very positive," "somewhat positive," "neutral," "negative," instead of a strict positive/negative classification.

Combines fuzzy logic with deep learning for better uncertainty handling.

Fuzzy Neural Networks (FNNs)

• Example: AI-based air quality monitoring predicts pollution levels using fuzzy categories (low, moderate, high, very high).

Converts raw predictions into fuzzy membership values for better interpretability.

Fuzzy Neural Networks (FNNs)

Applications of Uncertainty and Fuzziness in Deep Learning

This method in expert systems refers to a probabilistic simulation technique that relies on random sampling to approximate solutions to complex problems.

Monte Carlo Method

The Monte Carlo Method in expert systems refers to a probabilistic simulation technique that relies on ________ to approximate solutions to complex problems.

random sampling

It is commonly used in uncertain reasoning, decision-making, and risk assessment within expert systems.

Monte Carlo Method

ENUMERATE: How Monte Carlo Methods Work in Expert Systems

• Problem Representation

• Random Sampling

• Simulation & Computation

• Aggregation of Results

This part in Monte Carlo Methods in Expert Systems is where the expert system models an uncertain environment using probability distributions.

Problem Representation

This part in Monte Carlo Methods in Expert Systems is where a large number of random samples are generated based on these probability distributions.

Random Sampling

This part in Monte Carlo Methods in Expert Systems is where the system evaluates each sample using statistical or decision-making algorithms.

Simulation & Computation

This part in Monte Carlo Methods in Expert Systems is where the results from multiple simulations are combined to estimate probabilities, expected values, or optimal decisions.

Aggregation of Results

Applications of Monte Carlo in Expert Systems

• Medical Diagnosis: Estimating the likelihood of diseases based on uncertain symptoms.

• Network Security: Predicting attack probabilities in cybersecurity.

• Financial Risk Analysis: Assessing risks in investment decisions.

• AI Decision Support: Optimizing AI-driven decision-making under uncertainty.

Key Features of Monte Carlo Methods

• Uses random inputs to explore possible outcomes.

• Suitable for probabilistic or complex problems.

• Becomes more accurate with a larger number of simulations.

• Applied in fields like finance, physics, AI, and cryptography.

ENUMERATE: Types of Monte Carlo Algorithms

• Monte Carlo Integration

• Monte Carlo Optimization

• Monte Carlo Simulation

A types of Monte Carlo Algorithm is used to approximates definite integrals.

Monte Carlo Integration

A types of Monte Carlo Algorithm is used to solves optimization problems (e.g., Simulated Annealing).

Monte Carlo Optimization

A types of Monte Carlo Algorithm is used to models complex systems in finance, engineering, etc.

Monte Carlo Simulation

ENUMERATE: How This Handles Uncertainty in an Expert System

1. Simulates variations in medical test accuracy and disease prevalence using random sampling.

2. Models real-world uncertainty in expert systems where test results are not 100% reliable.

3. Estimates probabilities dynamically, instead of relying on fixed values, making the system more adaptive.

ENUMERATE: Why Use Monte Carlo in Expert Systems?

• Handles uncertainty and incomplete information well.

• Provides approximate solutions when exact solutions are infeasible.

• Improves decision-making accuracy by considering multiple scenarios.

TRUE OR FALSE

Both Monte Carlo simulations and "What If" scenarios are used for decision-making under uncertainty, but they differ in methodology and application.

TRUE

Uses random sampling and probabilistic models to simulate multiple possible outcomes.

Monte Carlo Simulation

Evaluates uncertainty by running thousands/millions of simulations with different random inputs.

Monte Carlo Simulation

Provides a distribution of possible results instead of a single outcome.

Monte Carlo Simulation

Analyzes specific hypothetical situations by manually changing input variables.

"What If" Scenarios

Helps understand the impact of specific decisions or events.

"What If" Scenarios

Focuses on a few predefined scenarios, not random variations.

"What If" Scenarios

This is a fundamental concept in probability theory used to update beliefs in the presence of new evidence.

Bayes’ Theorem

It helps in handling uncertainty by quantifying how the probability of an event changes when new data is available.

Bayes’ Theorem

Formula of Bayes’ Theorem:

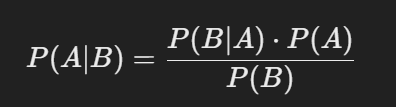
• P(A∣B) →_______

• P(B∣A) → _________

• P(A) → ________

• P(B) → __________

• P(A∣B) → Posterior Probability (updated probability after evidence)

• P(B∣A)P(B∣A) → Likelihood (probability of evidence given event)

• P(A)P(A) → Prior Probability (initial belief before evidence)

• P(B)P(B) → Evidence Probability (total probability of the evidence occurring)