Engng Math 145 Differential Equations
0.0(0)
0.0(0)
Card Sorting
1/3
There's no tags or description
Looks like no tags are added yet.
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
4 Terms
1
New cards
Seperable differential equations & solving
Put ouput variable on LHS and input on RHS
Times both side by dx and integrate (only RHS gets +C)
Make output variable subject of equation if possible
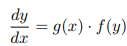
2
New cards
Linear differential equations & solving
Calculate I(x) = e∫P(x)dx (integrating factor)
[Multiply boths sides by I(x)]
Then: y = (1 / I(x)) * ∫ I(x) Q(x) dx
When calculating e∫P(x)dx no +C needed.
![<ol><li><p>Calculate I(x) = e<sup>∫P(x)dx</sup> (integrating factor)</p></li><li><p>[Multiply boths sides by I(x)]</p></li><li><p>Then: y = (1 / I(x)) * ∫ I(x) Q(x) dx</p></li></ol><p>When calculating e<sup>∫P(x)dx</sup> no +C needed.</p>](https://knowt-user-attachments.s3.amazonaws.com/992c189a-c67f-4b4d-a2da-be911eb2f600.png)
3
New cards
Word differential equations
Example:
Form V(t) = …
dy/dt = rate in - rate out → dy/dt = (ratein * concin) - (rateout * xconc) / V(t)
4
New cards
Differential equation notes
y’ = dy/dx & y’’ = d2y/dx2
“Initial value” is just values that should be used to find C.
For “solutions”, input into DE and see if equivalent.