meccanica - corpi rigidi

dammi la definizione di corpo rigido

Un corpo si dice rigido se la distanza tra qualsiasi sua coppia di punti è fissa. Ciò è dovuto ai legami interatomici che tengono fermi gli atomi.

quanti gradi di libertà ha un corpo rigido?

Fissato un punto A nel corpo rigido, abbiamo 3 coordinate (xyz).

Fissato un secondo punto B esso ha 2 gradi di libertà, perché ha distanza fissa da A.

Fissato un terzo punto C esso ha 1 grado di libertà, perché può solo che ruotare attorno la congiungente A-B.

Quindi in totale un corpo rigido ha 3 + 2 + 1 = 6 gradi di libertà

quali sono i tipi di moto che può compiere un corpo rigido? Dimostra una certa proprietà legata alle velocità

in generale il moto è una successione di coppie rotazione + traslazione infinitesime. In generale l’asse di rotazione cambia nel tempo, infatti viene detto asse di rotazione ISTANTANEO.

Quindi basta conoscere la velocita e la velocità angolare rispetto un asse del corpo per conoscere il suo moto in un istante.

La velocità dipende dalla psizionedella particella del corpo rispetto all’asse di rotazione, ma la velocità angolare no perché descrive l’angolo spazzato in un certo tempo

DIMOSTRAZIONE

Scelgo due punti all’interno del corpo, P e Q, mentre O è il punto per cui passa l’asse di rotazione, allora:

• v_P = v_o + w x OP

• v_Q = v_o + w x OQ

• v_P - v_Q = w x (OP-OQ = w x QP

  quindi v_P = v_Q + w x QP

per cui la velocità angolare è la stessa anche se ho scelto l’asse che passa per Q.

posizione del centro di massa per un corpo rigido?

dato che ρ = dm/dV e che m = ∫dm = ∫ρdV

r_CM = ∫rdm/∫dm = ∫rρdV/ ∫ρdV = 1/m ∫rρdV

se il corpo è OMOGENEO, quindi con ρ costante:

r_CM = ρ/m ∫rdV

quali sono le condizioni necessarie affinché avvenga l’equilibrio?

la somma vettoriale di tutte le forze esterne deve essere nulla, così come la somma di tutti i momenti delle forze esterni

quanti gradi di libertà ci sono nelle rotazioni attorno ad un asse fisso?

quando fisso un punto dell’asse perdo tre gradi di libertà, mentre se ne fisso un’altro (andando quindi a determinare l’asse di rotazione) ne perdo altri 2.

Dai sei gradi di libertà iniziali ne tolgo 5, per cui servirà un’unica equazione per determinare il moto di rotazione attorno ad un asse fisso.

rotazioni intorno ad un asse fisso: determina il momento assiale

uso la seconda equazione cardinale dL_o/dt = M_o

moltiplicandola per il versore u_z ottengo

dL_z/dt = dL_o u_z/dt = M_o u_z = M_z

rotazioni intorno ad un asse fisso: trova la formula che lega L_z a I_z, ovvero il momento angolare al momeno d’inerzia rispetto l’asse z. Cosa succede integrando ancora?rotazioni intorno ad un asse fisso:

So che ogni elemento ruota con velocità v = w x R (w perp. R)

Inoltre il momento angolare di dm è

• dL = r x p = r x dm v = r dm v u_T = r dm w R u_T

u_T = versore perpendicolare a r e v

• dL_z = dL u_z = r dm w R u_T u_z = r dm w R cos(pi/2 - θ) =

  r dm w R sinθ = dm w R²

integro:

• ∫dL_z = L_z = ∫ w R² dm = ∫ w (x² + y²) ρdV = I_z w

integrando ancora:

dL_z/dt = I_z dθ/dt = I_z α = M_z

rotazioni intorno ad un asse fisso: parla del moto del CM

il moto del CM è determinato perché dista R_CM dall’asse di rotazione, per cui:

• a_CM,T = α R_CM

• a_CM,N = w² R_CM

• v_CM = w R_CM

rotazioni intorno ad un asse fisso: ricava l’energia cinetica

K = ∫ ½ dm v² = ∫ ½ ρ v² dV = ∫ ½ ρ w² R² dV = ½ I_z w² = ½ L_z²/I_z

rotazioni intorno ad un asse fisso: teorema delle forze vive e potenza

dW = dK = I_z w dw = I_z dφ/dt dw = I_z dw/dt dφ = M_z dφ

P = dw/dt = M_z w

rotazioni intorno ad un asse fisso: generalizzazione di L_z

Se il moto è completamente determinato dal momento delle forze M_z, lo stesso non vale per il momento angolare L_z. Abbiamo che il momento angolare sia soltanto L_z solo nel momento in cui l’asse di rotazione è l’asse di simmetria.

L = I_z w

momento d’inerzia rispetto un asse di rotazione fisso

I = ∫ R² dm

dove R = distanza punto infinitesimo di massa dm-asse.

= ∫_V ρ R² dV

= ∫_V ρ (x²+y²) dV

momento d’inerzia rispetto all’asse di simmetria di un asta di lunghezza L

I = ∫_-L/2^L/2 x² dm = ∫ ρ x² dx = ρ (L³/24 + L³/24) = m L² / 12

momento d’inerzia rispetto all’asse di simmetria di un anello sottile di raggio R

I = ∫₀^2pi R² dm = ∫ ρ R² dl = ρ R² ∫ dl = ρ R² 2 pi R

circonferenza cerchio

ρ * circonferenza = massa, per cui

I = m R²

oppure

m = ρ * 2 pi R

I = ∫₀^2pi R² dm = ∫ R² R dθ ρ = 2 pi R³ ρ = m R²

momento d’inerzia rispetto all’asse di simmetria di un disco di raggio R

so che ρ = m / pi R²

I = ∫₀^R dr ∫₀^2pi dθ r r² ρ = 2 pi R⁴/4 ρ = ½ m R²

momento d’inerzia rispetto ad un asse di simmetria di un cilindro di raggio R e altezza L

ρ = m / pi R² L

I = ∫₀^R dr ∫₀^2pi dθ r ∫₀^L dz r² s =

= R⁴/4 2 pi L ρ = ½ m R²

momento d’inerzia rispetto ad un asse di simmetria di una sfera di raggio R

ρ = m / 4/3 pi R³

sin²θ = 1 - cos²θ

sinθdθ = -d cosθ

I = ∫₀^R dr ∫₀^pi dθ r sinθ ∫₀^2pi dφ (rsinθ)² ρ =

= 2 pi R⁵/5 ∫_-1¹ d cosθ (1 - cos²θ) ρ =

= 2 pi R⁵/5 (2-2/3) = 2 pi R⁵/5 4/3 m/(4/3 pi R³) = 2/5 R² m

enuncia e dimostra il teorema di Huygens - Steiner

il momento d’inerzia di un corpo rigido rispetto ad un asse che di trova a distanza D dal CM è dato dalla somma del momento di inerzia rispetto ad un asse parallela ma passante per il CM I₀ e del prodotto mD²

I = I₀ + mD²

DIMOSTRAZIONE

nuove coordinate di P:

z’ = z

x’ = x

y’ = y + D

I = ∫_V (x²+y²) dm =

passo alle coordinate del nuovo asse di rotazione

∫ [x’² + (y’ - D)²] dm =

svolgo il quadrato di binomio

∫ [x’² + y’² - 2Dy’ + D²] dm =

= ∫ (x’² + y’²) dm + D² ∫ dm - 2D ∫ y’ dm

• momento d’inerzia rispetto l’asse z’

• mD²

• nullo, perché =my’_CM con y’_CM la coordinata del CM è posta = 0

applicazione di huygens-steiner: calcola il momento d’inerzia di un’asta con punto fisso in uno degli estremi

I = I₀ + mD² = m L² / 12 + m L²/4 = m L² / 3

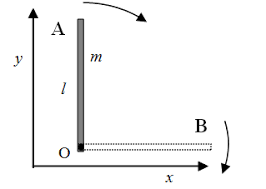
applicazione di huygens-steiner: calcola il momento d’inerzia di un disco con punto fisso in un estremo

I = I₀ + mD² = ½ m R² + mR² = 3/2 m R²

applicazione di huygens-steiner: calcola il momento d’inerzia di una sfera con punto fisso in un estremo

I = I₀ + mD² = 2/5 R² m + m R² = 7/5 R² m

applica il teorema di Huygens-Steiner all’enercia cinetica nel caso di una rotazione attorno ad un asse fisso che non passa per il centro di massa

K = ½ I w² =(H-S)= ½ (I_CM + mD²) w² = ½ I_CM w² + ½ m v²

Va a spiegare il teorema di Konig per l’energia cinetica, infatti

• energia cinetica NEL CM

• energia cinetica DEL CM

quando abbiamo un moto di precessione?

quando il momento angolare non è parallelo alla velocità angolare.

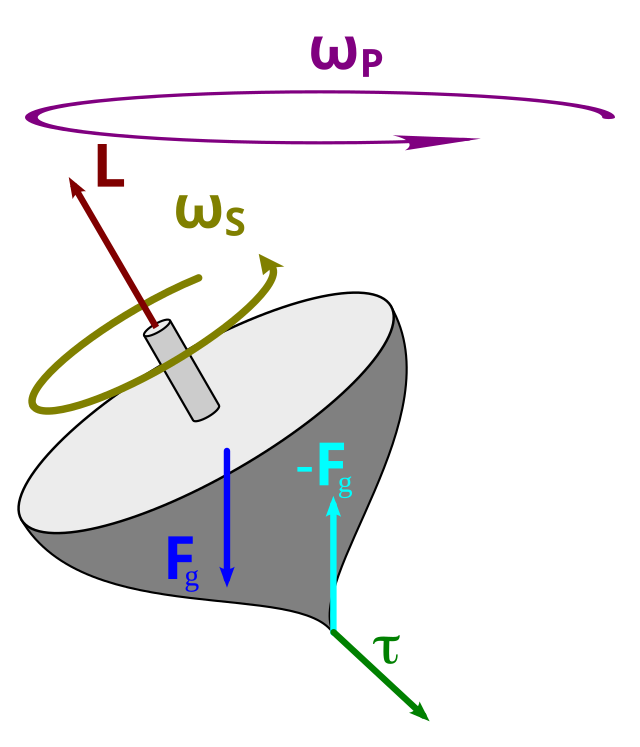
dimostra che la velocità angolare di precessione = velocità angolare di rotazione

considero due masse attaccate da un asta che ruotano sull’asse di rotazione che passa per il centro dell’asta, inclinato di un angolo θ rispetto l’asse.

so che la componente perpendicolare all’asse di rotazione del momento angolare L_p * w = 0

Poiché il moto delle due masse è circolare ci deve essere una forza che le spinge costantemente verso l’interno, ma:

• momento delle forze con forza peso: (r₂ = -r₁)

  r₁ x mg + r₂ x mg = (r₁ - r₁) x mg = 0

allora calcolo per una generica F, sapendo che F₂ = -F₁

• r₁ x F₁ + r₂ x F₂ = r₁ x F₁ + (-r₁) x (-F₁) =

  = 2r₁ x F₁ = M_tot

Che sappiamo essere perpendicolare al piano individuato da r e F (verso individuato dalla regola della mano destra)

Adesso studio il verso z:

dL_z/dt = M_z = 0 perché M è perpendicolare a w

quindi L_z si conserva

L = r₁ x mv₁ + r₂ x mv₂ = 2r₁ x mv₁

quindi L è perpendicolare al piano individuato dai vettori r e v.

F perp v

r x F perp r x v = M perp L = dL/dt perp L

per cui dz/dt = 0 e L * dL/dt = 0

quindi tutto L si conserva → anche L_p

Uso la formula di Poisson per cui esiste Ω perp a L_p e dL_p/dt tale che Ω x L_p = dL_p/dt

Ma L è perpendicolare alla sbarra e ruota con essa, quindi anche L_p ruota con w e pertanto w = Ω

quando avviene un moto di puro rotolamento?

Quando un corpo ruota senza strisciare attorno al punto di contatto

Come si calcola l’energia cinetica di un corpo in moto di puro rotolamento?

K = ½ I_c w² = (H-S) = ½ m v²_CM + ½ I_CM w²

= ½ m (wR)² + ½ I_CM w²