binomial expansion (y1)

binomial expansion

the process of expanding (a+b)^n expressions

pascal’s triangle

used to help binomial expansion- the (n+1)th row gives the coefficients in the expansion of (a+b)^n

formed by adding adjacent pairs of numbers to find the numbers on the next row

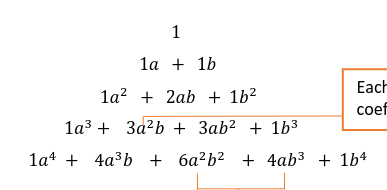
factorial notation

n! used to help binomial expansion, quicker than Pascal's Triangle for larger indices

nCr

nCr = n!/r!(n-r)!

gives the coefficient for the rth term for (kx+c)^n

the rth entry in the nth row of pascal's triangle is given by (n-1)C(r-1)

binomial expansion

a rule allowing for the quick expansion of brackets e.x.

(a+b)^n = a^n + (nC1)a^(n-1)b + (nC2)a(n-2)b^2 ...

finding coefficiencts

the coefficient of x^n in the binomial expansion (kx + c)^m is:

(mCn)(k^n)(c^(m-n))

binomial estimation

when x is less than 1, larger powers can be ignored to produce an estimation of the value of a binomial expression as their value will be negligible

the amount of terms to include in the estimation will usually be provided, but if it is not 3 terms is a suitable number