AP Statistics Ultimate Review

Observational Studies claim….

Correlation! (not causation)

how to design an experiment

S- start with the subjects

R- randomly assign them (big bag shake well)

T- treatments (state them)

M- measure

E- each subjects response to them

C- compare their

A/P- average or proportion

Experiments

Can claim causation if they have control, randomization, and repetition

Types of Experiments

Completely Randomized- each participant is assigned to a treatment group randomly.

Randomized block- participants are divided into blocks based on a trait, and randomization occurs within each block.

Matched Pairs- participants are paired based on similar characteristics, and each receives a different treatment. (think twins)

What are Factors and Levels

Factors- independent variables (treatments) in an experiment that are manipulated. (Ex. Exercise)

Levels- the different values or conditions of a factor. (ex. High, medium, low)

Confounding vs. Lurking Variables

Confounding- affect both the treatment and the response, making it difficult to determine the true effect of the treatment.

Lurking- variables that are not included in the study, but may affect the outcome.

Measures of Spread and Outliers

IQR: middle 50% of the data found by Q3-Q1

Upper Fence/ Outliers: Q3+1.5(IQR)

Lower Fence/ Outliers: Q1-1.5(IQR)

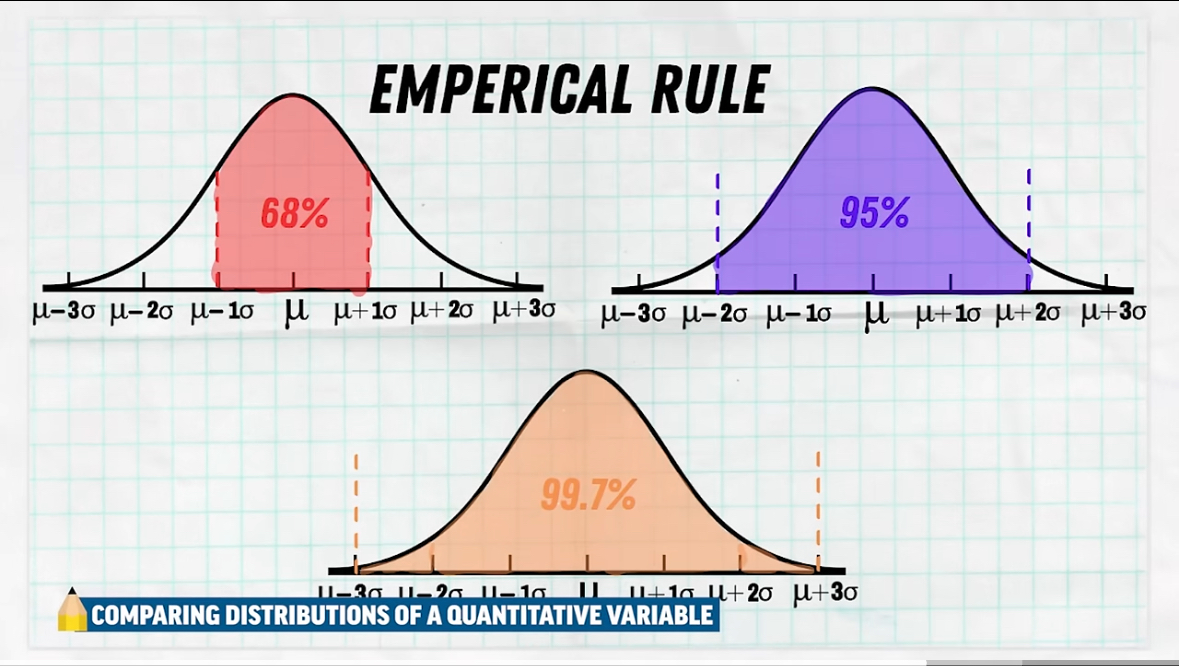
Normal Model Information

Outliers: Mean ± 2(standard deviation)

Describing linear association (r-value)

There is a (strength), (positive or negative), linear relationship between x and y (in context)

interpret the coefficient of determination (r²)

___% of the variation in y (in context) can be explained by the changes in x (in context)

interpret the slope

for every 1 increase in the x (in context) the predicted y (in context) increases or decreases this much

interpret the y intercept

when the x is zero the predicted y is this (list x and y in context)

extrapolation

making a prediction outside of the domain of the provided data. this is dangerous!

leverage point on LSRL

point far away from the mean of x

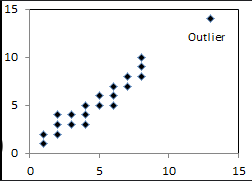
influential point on LSRL

point with high leverage that is not in line with the rest of the data removing it has a significant impact on the slope the LSRL

Standard deviation of the residuals

average amount the actual y varies from the predicted y in LSRL

how to compute residual

Actual y- Predicted y

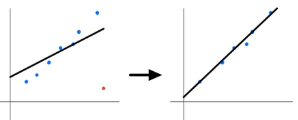
what does a pattern on a residual plot mean

A linear model is not appropriate

Understand how to read a computer printout

To find LSRL equation without a table

slope= r(std. deviation of y/ standard deviation of x)

then set up an equation using x bar and y bar to solve for y intercept.

Geometric Distribution

go until a success

Binomial distribution

success out of a set number of trials.

How to check for independence

P(A)= P(A|B)

what is given probability/ P(A I B)

P(A and B) / P(B)

What is the difference between U and Upside down U

U= “or”/addition

Upside Down U= “and”/ multiply

What is the sum of all probabilities

ONE

what are disjoint/ mutually exclusive events

Events that cannot happen at the same time.

If events are disjoint then P(A or B)= P(A)+P(B)

what are independent events

Events where the occurrence of one does not affect the probability of the other. For independent events, P(A and B) = P(A) × P(B).

If events are not disjoint (“or” formula)

P(A(or B) = P(A) + P(B) - P(A and B)

If events are not independent (“and” formula)

P(A and B)= P(A) x P(B|A)

when to use geometric pdf

when looking for the probability of an EXACT place of the first success

when to use geometric pdf (up to place of success)

to find probability of 1st success happening on or before a certain place

when to use 1- geometric cdf (lower part you don’t want)

to find probability of 1st success happening on or after a certain place

when to use binomial pdf

to find probability of an exact number of successes

when to use binomial cdf (up to and including the # of successes you want)

to find the probability of less than or at most a certain # of successes

when to use 1- binomial cdf (lower part you do not want)

to find the probability of more than or at least a certain # of successes

How to find an expected value

multiply each x by their frequency and add all together.

x₁(p₁)+x₂(p₂)+…= M_x

What is center effected by

addition, subtraction, multiplication, and division

What are measures of spread (standard deviation) affected by

Multiplication and division

How do you combine means together

add or subtract them like normal

how do you combine (add or subtract) standard deviations

std.dev_x+y= sqrt. of ((std. dev x)² + (std.dev y)²)

describing the shape of a sampling distribution (for proportions)

Shape: unimodal, symmetric

Outliers: N/A

Center: M_{p hat}= P (aka population proportion)

Spread: standard deviation of the population ( sqrt. of ((p(1-p)/n)0

describe the distribution (for means)

Shape: unimodal, symmetric

Outliers: N/A

Center: M_{x bar}= M (aka population mean)

Spread: standard deviation of the population (standard deviation/ sqrt. of n)

Assumptions and conditions (proportions)

Random- stated or assumed

Independent- n ≤ 10% of population

Large Enough- np ≥ 10

n(1-p) ≥ 10

Assumptions and conditions (means)

Random- stated or assumed

Independent- n ≤ 10% of population

Large Enough- n >30

what is PANIC used for and what does it stand for

runs a confidence interval

P- State the parameter(s) (M= or P=)

A- Assumptions and Conditions

N- Name of the interval

I- find/calculate the interval

C- write conclusion

what to do if n isn’t >30 (means)

make a frequency dot plot and determine if it is

S- Somewhat Symmetric

U- Unimodal

N- No outliers

if it is and other conditions are met then approx. normal model applies

calculating a one proportion z-interval

statistic ± z* (standard deviation)

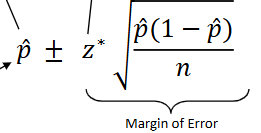
to find critical value (z-distribution)

invnorm(onetail)

ex. z* for 95% confidence interval= invnorm(.025)

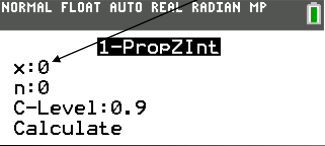
one proportion z-interval in calculator

x: number of successes

n: total number of trials

c-level: desired confidence level

two proportion z-interval formula

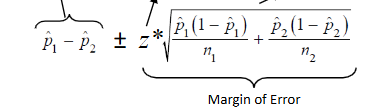
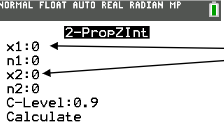
two proportion z interval calculator

x1: number of successes

n1: total number of trials

x2: number of successes

n2: total number of trials

c-level: desired confidence level

Confidence interval 1 proportion conclusion

i am % confident that the true proportion of ____ is between ___% and ___%

Confidence interval 2 proportion conclusion

i am % confident that the true proportion of ____ is between ___% and ___% lower/higher for __-.

AND

Since zero is not in the interval there is evidence of a significant diff. between ___ and ____

OR

Since zero is in the interval there is not evidence of a significant diff. between ___ and ___.

Effects of higher confidence level

larger critical value and wider interval

what to do if no p-value is given

“dont cry use .5”

What is PHANTOMS and what does it stand for

model for hypothesis test

P- parameter(s) (P= or M=)

H- Hypothesis (H_o= 0 or no difference, H_a= new claim)
A- Assumptions (get RIL)

N- name of test

T- find test statistic

O- obtain p-value

M- make decision (reject or fail to reject H_o)
S- state conclusion

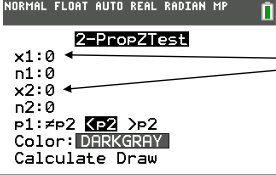
one proportion z-test formula

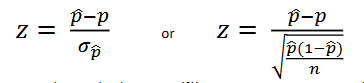
two proportion z test calculator

x1: number of successes

n1: total number of trials

x2: number of successes

n2: total number of trials

p1: ≠p2, <p2, >p2

when to reject H_o

when p-value is < alpha (.05)

when to fail to reject H_o

when p-value is > alpha (.05)

when to use t- distribution

when we do not have the standard deviation of the population.

how to calculate degrees of freedom (t-distribution)

df=n-1

one mean t-interval formula

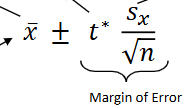
computing critical value (t distribution)

invT(one tail)

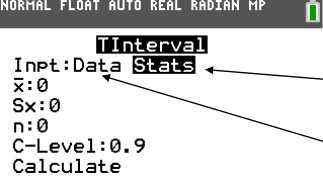
one mean t-interval calculator

STATS-

x̅: sample average

S_x: standard error

n: sample size

c-level: desired confidence level

IF GIVEN TABLE-

enter data into L1and L2 and use “Data” instead

hypothesis test conclusion

Since p value is ___ I reject/fail to reject H_o.

There is/is not significant evidence proving H_a (in context)

two mean t-interval formula

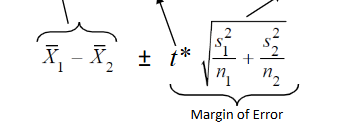
two mean t-interval conclusion

i am % confident that the true average of ____ is between ___ and ___ lower/higher for __-.

AND

Since zero is not in the interval there is evidence of a significant diff. between ___ and ____

OR

Since zero is in the interval there is not evidence of a significant diff. between ___ and ___.

one mean t-test formula

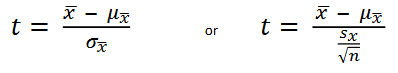
one mean t test calculator

H_o: null hypothesis

x̅: sample mean

S_x: standard error

n: sample size

M: ≠ H_{o, <} H_{o, >} H_o

2 sample t test calculator

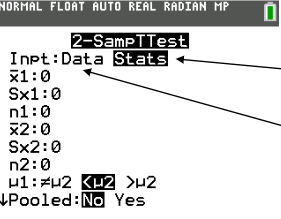
when to use matched pairs

1 sample of subjects and 2 pieces of related data. you are interested in the DIFFERENCE in between the data. ( in your calculator you will use a 1 mean t-test/interval and enter the data of the difference)

Matched pairs interval conclusion

I am ___% confident that the average difference in ___ is between ___ and ___ lower/higher for ___

Matched pairs test conclusion

Since p-value is ___ I reject/ fail to reject H_o.

There is/ is not evidence that the average difference in ___ is significantly different.

Assumptions for two samples of data

Get RIL for each data sample AND include that the samples are independent of each other (in context)

Type 1 error

Rejected the null hypothesis when it was actually true

Type 2 error

Not rejecting the null hypothesis when it is actually false.

What is Power

the probability of rejecting the null hypothesis when it is false

What is the relationship between Power and Beta

Power+Beta=1

What is Beta

Probability of a Type 2 error

What is alpha

probability of a Type 1 error

Effects of increasing alpha

probability of a Type 1 error increases

probability of a type 2 error decreases

Power increases

Effects of increasing sample size

probability of type 1 error stays the same

probability of type 2 error decreases

power increases

when to run chi square Goodness of fit test

• one sample

• one categorical variable

H_o= the claimed distribution is correct

when to run chi square test of homogeneity

• 2 samples (from different populations)

• one categorical variable (checking for sameness)

H_o= each population is having the same rate for every category of the variable

Expected values for chi square test formula

((row total)(column total))/(total toal)

Chi square degrees of freedom formula

df= (row-1)(column-1)

when to run chi square test of independence

• one sample

• two categorical variables (sorted by categories)

H_o= the two variables are independent of each other/ no association/ no relationship

Empirical rule