AP Calc Flashcards

DIsplacement of the particle or net distance traveled by the particle, over the time interval [a,b]

$$\int_{t1}^{t2}\!v\left(t\right)\,dt$$

Is defined as the difference between the final and initial positions of the particle. It can be calculated as the integral of the velocity function over the given interval.

Total Distance traveled by the particle over the time interval [a,b]

$$\int_{t1}^{t2}\!\left|v\left(t\right)\right|\,dt$$

Neglects the (-) b/c of the absolute.

Position

x(t) or s(t)

$$\int_{}^{}\!v\left(t\right)\,dt$$

Velocity

v(t) or s’(t)

$$\int_{}^{}\!a\left(t\right)\,dt$$

Acceleration

v’(t) or s’’(t)

Average value over a continuous function f over an interval [a,b]

$$\frac{1}{b-a}\int_{a}^{b}f\left(x\right)\!\,dx$$

Is calculated by taking the integral of the function over the interval and then dividing by the width of the interval.

When do limits exist?

Limits exist only if the left and right are equal

Cases when limits DNE

• $$\frac{\left\vert x\right\vert}{x}$$

  • Behavior differs from left-hand ≠ right-hand

• $$\frac{1}{x}$$

  • Vertical Asymptote (infinite limit) [unbounded behavior]

• $$Sin\left(\frac{1}{x}\right)$$

  • Oscillation: “Bouncing between multiple values”

Derivative Rule for $e^{x}$

$$e^{x}$$

Derivative Rule for $\ln x$

$$\frac{1}{x}$$

Derivative Rule for $\sin x$

$$\cos x$$

Derivative Rule for $\cos x$

$$-\sin x$$

Derivative Rule for tan x

sec² x

Derivative Rule for sec x

sec x tan x

Derivative Rule for csc x

-csc x cot x

Derivative Rule for cot x

-csc² x

Inverse Trig Derivatives: arcsin x

$$\frac{1}{\sqrt{1-x^2}}$$

Inverse Trig Derivatives: arccos x

$$\frac{-1}{\sqrt{1-x^2}}$$

Inverse Trig Derivatives: arctanx

$$\frac{1}{1+x^2}$$

Inverse Trig Derivatives: arccot x

$$\frac{-1}{1+x^2}$$

Inverse Trig Derivatives: arcsec x

$$\frac{1}{x\sqrt{x^2-1}}$$

Inverse Trig Derivatives: arccsc x

$$\frac{-1}{x\sqrt{x^2-1}}$$

The position vector at time t is

r(t) = <x(t), y(t)>

The velocity at time t is

v(t) = <x^’(t), y^’(t)>

The displacement vector

<\int_{a}^{b}\!x^{^{\prime}}\left(t\right)\,dt,\int_{a}^{b}\!y^{^{\prime}}\left(t\right)\,dt>

Speed of the particle at time t

$$s\left(t\right)=\sqrt{\left\lbrack x^{^{\prime}}\left(t\right)\right\rbrack^2+\left\lbrack y^{^{\prime}}\left(t\right)\right\rbrack^2}$$

The distance traveled

$$\int_{a}^{b}\sqrt{\left\lbrack x^{^{\prime}}\left(t\right)\right\rbrack^2+\left\lbrack y^{\prime}\left(t\right)\right\rbrack^2}\!\,dt$$

The acceleration vector of the particle

a\left(t\right)=<x^{\doubleprime}\left(t\right),y^{\doubleprime}\left(t\right)>

The relationship between polar coordinates & standard rectangular coordinates (x,y) #1

$$x=r\cos\theta$$

The relationship between polar coordinates & standard rectangular coordinates (x,y) #2

$$y=r\sin\theta$$

The relationship between polar coordinates & standard rectangular coordinates (x,y) #3

$$r^2=x^2+y^2$$

The relationship between polar coordinates & standard rectangular coordinates (x,y) #4

$$\tan\theta=\frac{y}{x}$$

What is a sequence

A function f(n) whose domain consists only of nonnegative integers.

a_n = f(n)

When does a sequence converge to L

$\lim_{n\rightarrow\infty}$ a_n = L & diverges if this limit is $\infty$ or DNE

Test: n^th Term Test

A method to determine the convergence or divergence of a series by examining the limit of its terms as n approaches infinity. If the limit does not equal zero, the series diverges; if it equals zero, the test is inconclusive.

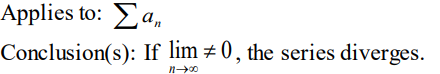
Test: Integral Test

Used to determine convergence or divergence of series with positive terms by comparing it to an improper integral.

Test: Direct Comparison Test

A method for assessing the convergence or divergence of a series by comparing it to a second series, which is known to converge or diverge. If the first series is smaller than a convergent series, it also converges; if larger than a divergent series, it diverges.

Test: Limit Comparison Test

A convergence test used to compare the limit of the ratio of the terms of two series as n approaches infinity. If the limit is positive and finite, both series either converge or diverge together.

Test: Alternating Series Test