Math Formulas (Secant/Tangent/Area/Variation)

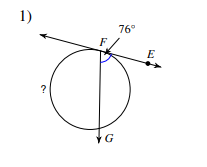
Secant - Tangent (INSIDE ANGLE)

Arc / 2 = Angle

Secant - Tangent (OUTSIDE ANGLE)

(Major arc - Minor Arc) / 2 = Angle

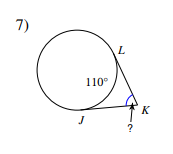
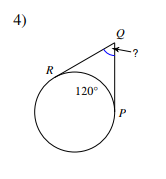
Tangent - Tangent (OUTSIDE ANGLE)

(Major arc - Minor Arc) / 2 = Angle

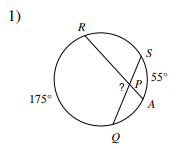
Secant - Secant (FORMS AN X)

(Arc + Arc) / 2 = Angle

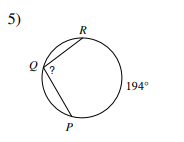
Secant - Secant (ANGLE POINT IS ON THE CIRCLE)

Arc / 2 = Angle

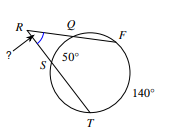
Secant - Secant (ANGLE OUTSIDE)

(Arc - Arc) / 2 = Angle

Area Circle Formula

π radius²

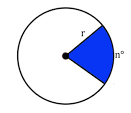
Area of a Sector

(measure of the arc / 360) (π radius²) = Sector

Area of a Triangle

(Height)(Base) / 2 = Area

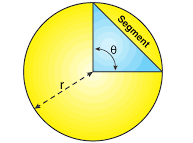
Area of a Segment

(measure of the arc / 360) (π radius²) - (B)(H) / 2 = Segment

Direct Variation

Y varies directly as X, or Y is directly proportional to X, also K is there as a constant.

Y = KX

Usually whatever is mentioned first takes the place of Y

Finding K or the Constant

K = Y / X

Inverse Variation

Y varies inversely as X, or Y is inversely proportionate to X, also K is there as a constant.

Y = K / X

Finding K

K = XY

Joint Variation

If the ratio of Y to the product of two or more variables is constant, then Y varies jointly as the other variables. Y varies jointly as X and Z, also K is there as a constant.

Y = KXZ

*UNLIKE DIRECT OR INVERSE YOU DON’T FLIP THE FORMULA FOR K!

Y = 32, X = 8, Z = 2

32 = K(8)(2) → 32 = 16K → Divide by 16 to isolate K → 2 = K

Combined Variation

Y varies directly with X and inversely with Z, also K is there as a constant.

Y = KX / Z

Finding K

*UNLIKE DIRECT OR INVERSE YOU DON’T FLIP THE FORMULA FOR K!

Y = 10, X = 5, Z = 2

10 = K(5) / 2 → Multiply by 2 on both sides to remove fraction → 20 = 5K → Divide by 5 to isolate K → 4 = K

Radical to Exponent and reverse

^n√a^m → a^n/m

n = index
m = radicand’s exponent
a = radicand

n becomes the denominator of m in exponent form.

³√8² → 8²/³

RADICAL MULTIPLICATION 3 CASES

1) Same index, different Radicand.

Multiply the insides and outsides then simplify.

√2 x √2 = √4 → 2

2) Different index, same radicand.

Multiply the index, add the index, simplify.

√2 × ³√2 → (3 × 2) and (3 + 2) → ^6√2^5 → ^6√32

3) Different Index, Different Radicand

FORMULA: ^n√a x ^m√b = ^n(m)√a^m x b^n

*Basically the exponents swap.

√3 x ³√2 → ^6√3³x2² → ^6√108

RADICAL DIVISION

FORMULA: ^n√a / ^n√b = ^n√a / b

CONJUGATION

Getting the inverse of the equation then multiplying them together using FOIL.