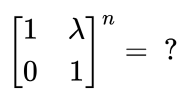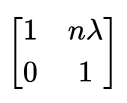Matrices and Determinants

What’s an Idempotent Matrix?

An idempotent matrix is a square matrix that, when multiplied by itself, yields the same matrix. In other words, if A is an idempotent matrix, then A² = A.

What’s an Involuntary Matrix?

An involuntary matrix is a square matrix that, when squared, yields the identity matrix. This means that if B is an involuntary matrix, then B² = I, where I is the identity matrix.

What’s an Orthogonal Matrix?

An orthogonal matrix is a square matrix whose rows and columns are orthogonal unit vectors. This implies that when an orthogonal matrix is multiplied by its transpose, the result is the identity matrix.

What’s a Periodic Matrix?

A matrix where A^k+1 = A

‘k’ is the period of the matrix.

What’s a Nilpotent Matrix?

A nilpotent matrix is a square matrix N such that for some positive integer k, N^k = 0, where 0 is the zero matrix. This indicates that the matrix becomes zero when raised to a certain power.

Important: N^k-1 ≠ 0.

What is the determinant of an Idempotent Matrix?

The determinant of an idempotent matrix is either 0 or 1.

What is the determinant of an Involuntary Matrix?

The determinant of an involutory matrix is either 1 or -1.

What is the determinant of an Orthogonal Matrix?

The determinant of an orthogonal matrix is either 1 or -1.

What is the periodicity of an Idempotent Matrix?

An idempotent matrix has a periodicity of 1.

What is the determinant of a Nilpotent Matrix?

The determinant of a nilpotent matrix is always 0.

(A^T)^T = ?

A

(A+B)^T = ?

A^T + B^T

(ABC)^T = ?

C^TB^TA^T

(kA)^T = ?

k(A)^T

Maximum number of different elements a symmetric matrix can have?

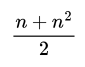
What is the trace of a matrix?

The trace of a matrix is the sum of the elements on its main diagonal. It is only defined for square matrices.

Tr(A+B) = ?

Tr(A) + Tr(B)

Tr(A^T) = ?

Tr(A)

Tr(λA) = ?

λTr(A) for scalar λ

Tr(AB) = ?

Tr(A)Tr(B) for compatible matrices A and B.

Also Tr(AB).

|A^T| = ?

|A|

If any two rows/columns are identical, how does that affect the value of the determinant?

The determinant is equal to zero, indicating that the matrix is singular.

The interchange of any two consecutive rows or columns will affect the value of the determinant how?

The determinant will change its sign.

If a scalar is multiplied to the determinant:

The scalar will be multiplied to any one row or column.

|kA| = ?

kⁿ |A|, where n is the order of the matrix.

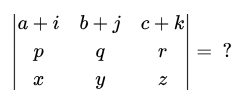
That’s why row operations work!

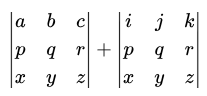
|AB| = ?

|A| |B|

if they are of the same order then it’s also |BA|

|A^T| = ?

|A|

|kA| = ?

kⁿ|A|, where n is the order of matrix A.

|Aⁿ| = ?

|A|ⁿ

A * adj(A) = ?

|A|I, where I is the identity matrix.

adj(A^T) = ?

[adj(A)]^T

adj(AB) = ?

adj(B) * adj(A)

adj(adj(A)) = ?

|A|^n-2 A, where n is the order of the matrix.

adj(kA) = ?

k^n-1 adj(A), where n is the order of the matrix.

|adj(A)|

|A|^n-1, where n is the order of the matrix.

|adj(adj(A))|

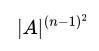
|adj(…..(adj(A)))| = ?

where it occurs ‘r’ times.

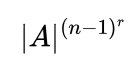
|A * adj(A)|

|A|ⁿ where n is the order of the matrix A.

adj(adj(A)) for 2×2 matrices?

A

adj(adj(adj(A))) for 2×2 matrices?

adj(A)

A^-1 = ?

adj(A)

|A|

(A^-1)^-1 = ?

A

(A^T)^-1 = ?

(A^-1)^T

(A^-1)ⁿ = ?

(Aⁿ)^-1

(AB)^-1 = ?

B^-1 A^-1

(kA)^-1 = ?

k^-1 A^-1 = A^-1/k

|A^-1| = ?

|A|^-1 = 1/|A|

How do you find the characteristic equation of a matrix?

|A - λI| = 0

You can tell the order of a matrix from its characteristic equation how?

The order of a matrix is the degree of its characteristic polynomial, which corresponds to the highest power of λ in the equation |A - λI| = 0.

In the characteristic equation of a matrix, the coefficient of I (Identity matrix) is:

(-1)ⁿ |A|, where n is the order of the matrix.

How do you know if a homogenous system of equations has a unique solution?

Δx = Δy = Δz = 0 and Δ≠0

This is called a trivial solution.

How do you know if a homogenous system of equations has infinite solutions?

Δx = Δy = Δz = 0 and Δ=0

This is called a non-trivial solution.

Do you know how to differentiate a determinant, or multiply two determinants?

Yes please!