A5 Galilean and Special Relativity

Galilean and Special Relativity

A5.1 Speed of Light

3×10⁸ ms^-1

A5.2 Reference frames

Viewpoint; set of coordinates to record position and time of events, at this point, stationary, everything else is moving relative to you.

A5.3 Inertial reference frames

Non-accelerating; constant velocity with respect to each other; No such thing as an absolute reference frame in the universe. No place completely stationaey; everything moves relative to everything else.

A5.4 Dumbass calculating relative v’s

V_ab = speed of a relative to b
V_ba = -V_ab.
V_ab + V_bc = V_ac

A5.5 Newton’s 1st postulate

Laws of physics are same in any inertial reference frame, every reference frame is correct, no absolute one.

A5.6 Galilean transformation explained

For small speeds much smaller than c:

Velocity, position (and time), appear differently from different reference frames

x , y , t is reference frame S.
x^’ , y^’ , t^’ in S^’

A5.7 Equations Galilean

x^’ = x - vt
y = y^’. , z = z^’ t = t^’

u^’ = u - v

v + u^’ = u = v_ag + v_gb = v_ab
(u = v_ab) ( u^’ = v_gb) (v = v_ag)

A5.8 Space time relativity

Close to speed of light; space and time become relative; time/length dependant on ref. frame.

A5.9 2^nd postulate of relativity

Speed of light in vacuum is constant in all inertial reference frames. never anything large than c, and flashlight is same speed of light whether in moving frame or stat.

A5.10 Lorentz factor

Correcting galilean transformations for speeds close to c, by multiplying by scaling factor; Lorentz ; γ = ¹/ sqrt (1 - v²/_c²)

always greater than 1. Needed for time dilation and length contractions

A5.11 Lorentz Transformation

x = γ (x^’ + vt^’), ——— x^’ , t^‘ is as measured from moving frame.

x^’ = γ (x - vt)

t = γ (t’ + ^vx’/_c²)

t’ = γ (t - ^vx/_c²)

y = y’, z = z’

A5.12 Velocity addition transformations (Lorentz)

u’ = ^(u+v)/_{(1- uv/c²)}
u ^{= (u’+v)}/_1+u’v/c²

u = v_ag, u’ = v_ab, v = v_gb

A5.13 Space-Time-Intervals

(delta)s. Reference frames non absolute. Some quantities invariant in all inertial reference frames; Proper time: t_o, Proper length: L_o, Space time interval: (delta)s
s² = ct² - x² (t,s,x are delta’s; changes in)
s = invariant

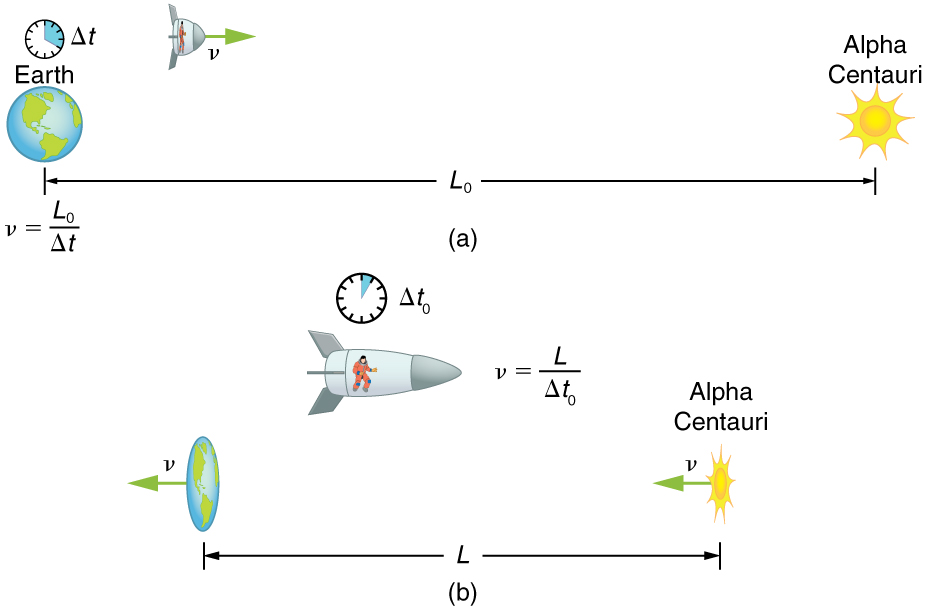
A5.14 Proper time/length

t_o = time interval between 2 events measured from reference frame in which the events are in same place (ref frame of moving object - rocket; S’)
t = t_oγ (dilated)

(time goes by slower when moving faster)

L_o = length measured in ref. frame where object is at rest (to observer) - earth: S
L = L_o/γ (contracted)

(lengths are smaller when moving faster)

A5.15 Simultaneity

Whether two spatially simultaneous (same t) events happen at the same time is not absolute, but depends on the observer's reference frame 

use spacetime to determine.

A5.16 Space-time diagrams

Represent objects motion in time

ct vs x
Lines drawn = worldlines: any ct’
Grad of ct’ = ^c/_v (v = ^x/_t) = steep=slow
ct = x = speed of light.
if any point below v = c line; non causual events
Grad never below 1.
ct’ and x’ represent coordinate in S’ frame (moving at v rel. to S)
Parralel lines to x’ and ct’ help to determine coordinate

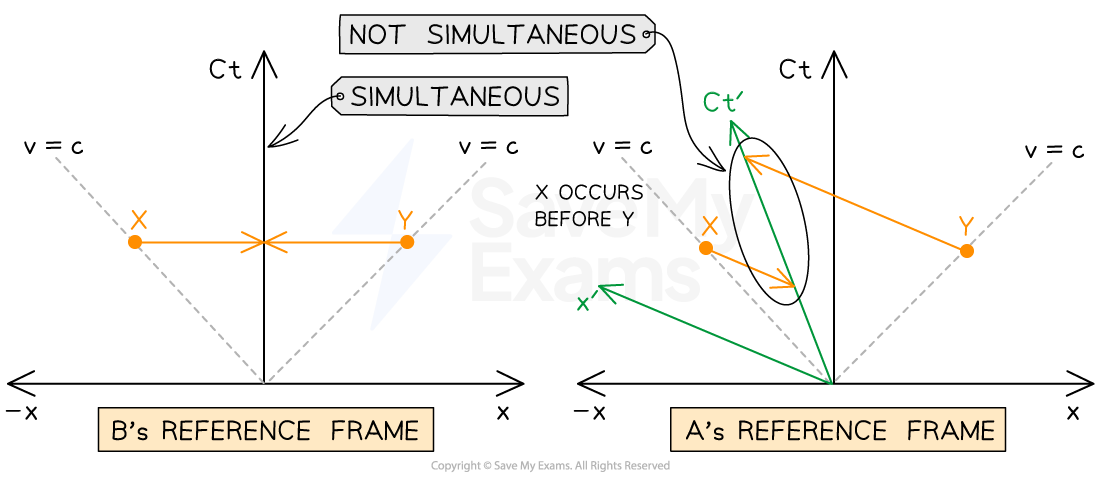
A5.17 Simultaneity in diagrams

dependent on ref. frame whether 2 or more events are simultaneous, see diagram

A5.18 Length contr Time dil in diagrams

If in S ref frame same place t_o seperated, see that in S’ event t seperated; bigger, and happens to the left of the first events.

If in S ref frame length L_,

A5.20 Muons

Muon: unstable subatomic particle , 200x mass of e^- . Travel at 0.98c and half life of 1.6 µs. Distance of one half life - 470 m. But, then we wouldnt detect any on earth, but we do… (10km from emission to detection). We expect like very little muons because 21 half lives in that spacetime. The fact that we detect muons even is due to time dilation:

A5.21 Muon decay; time dilation

γ = 5.
Therefore on earths ref frame; t = 4.3 half lives, instead of 21. So more muons detected than expected through Newtonian physics.
L measured by muon is also less than 10km; 2km actually, so 4.3 half lives