geometry regents

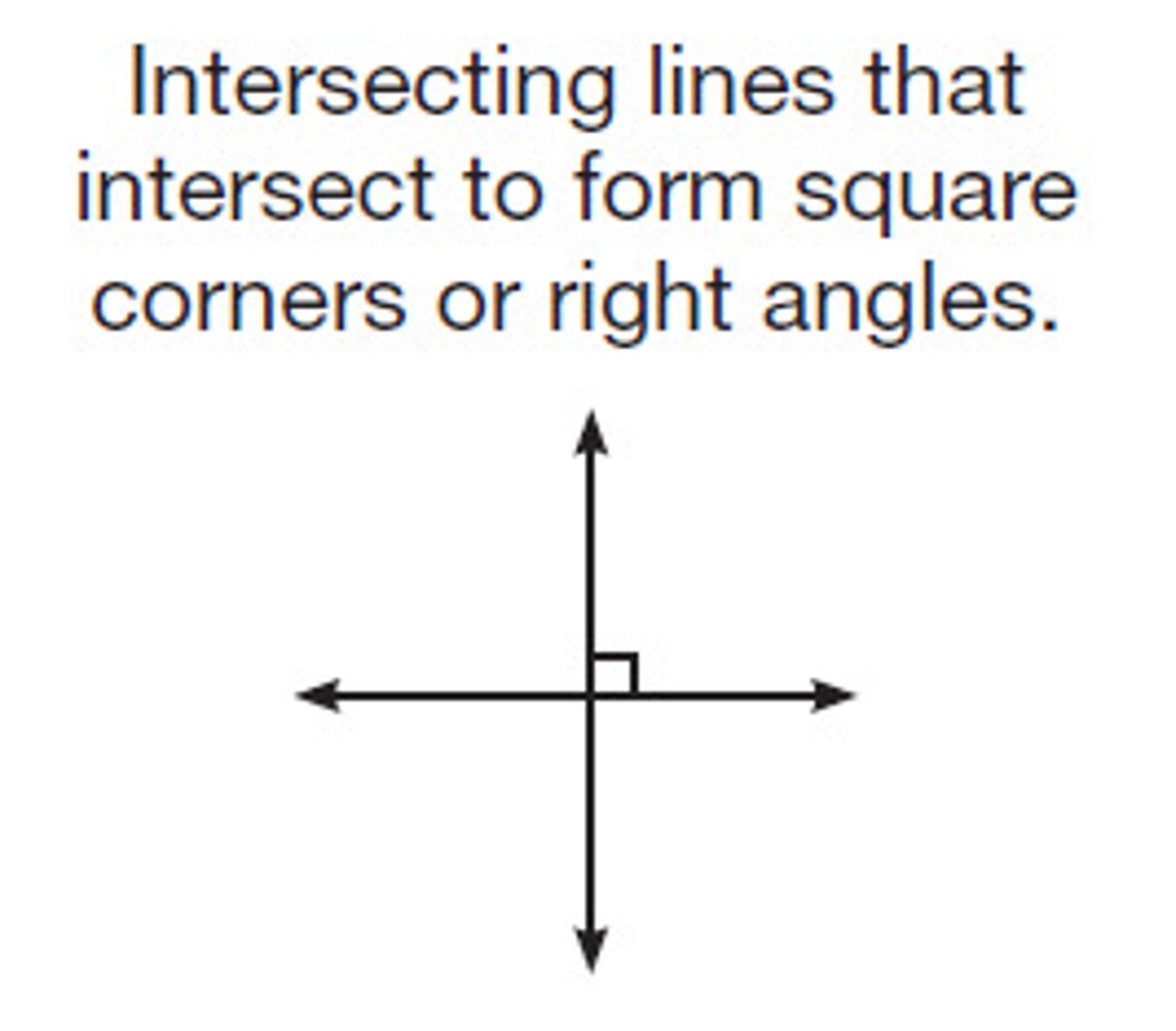
Perpendicular lines form what angles?

Right angles

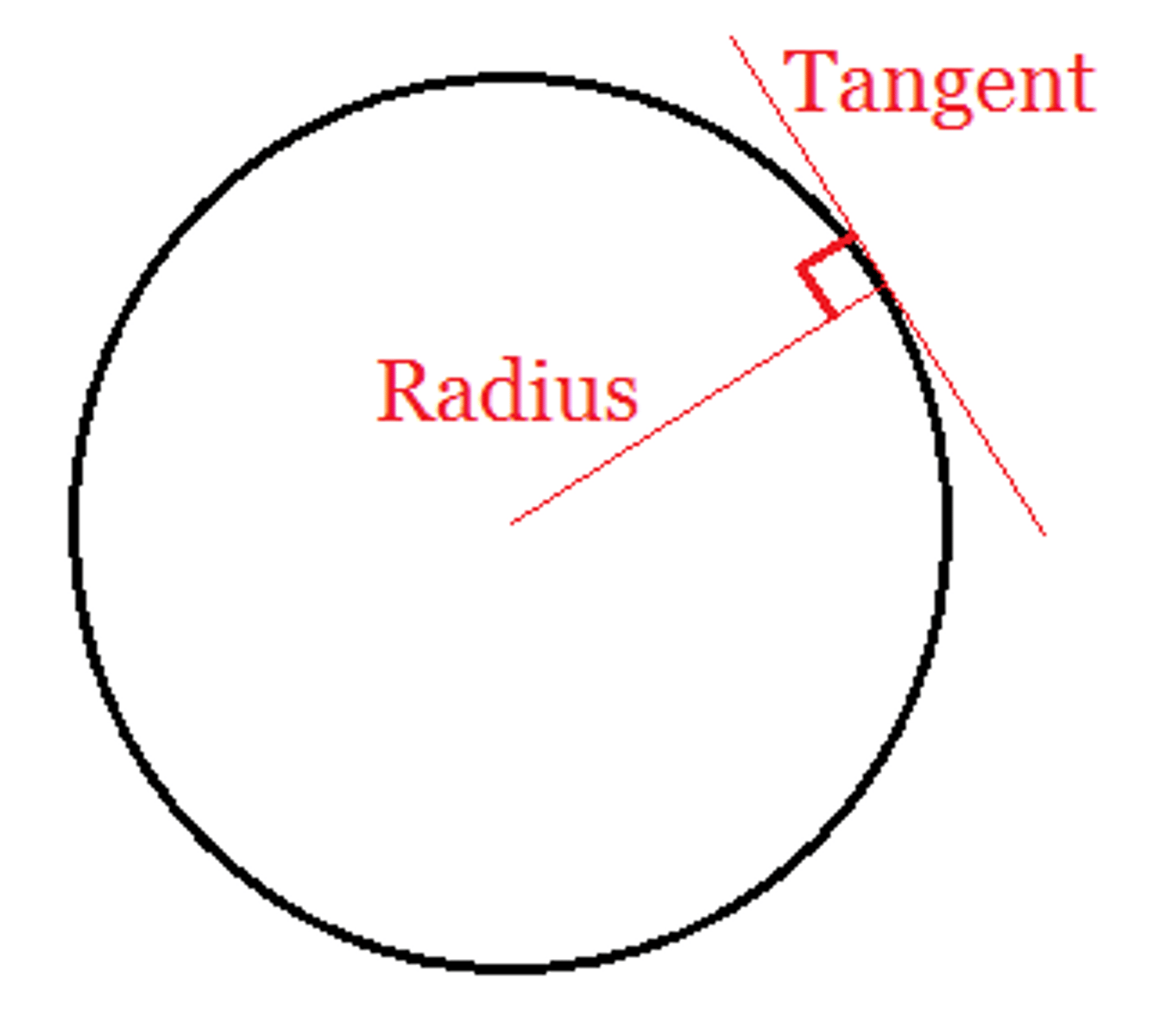
Radii and tangents in circles form what angles?

Right angles

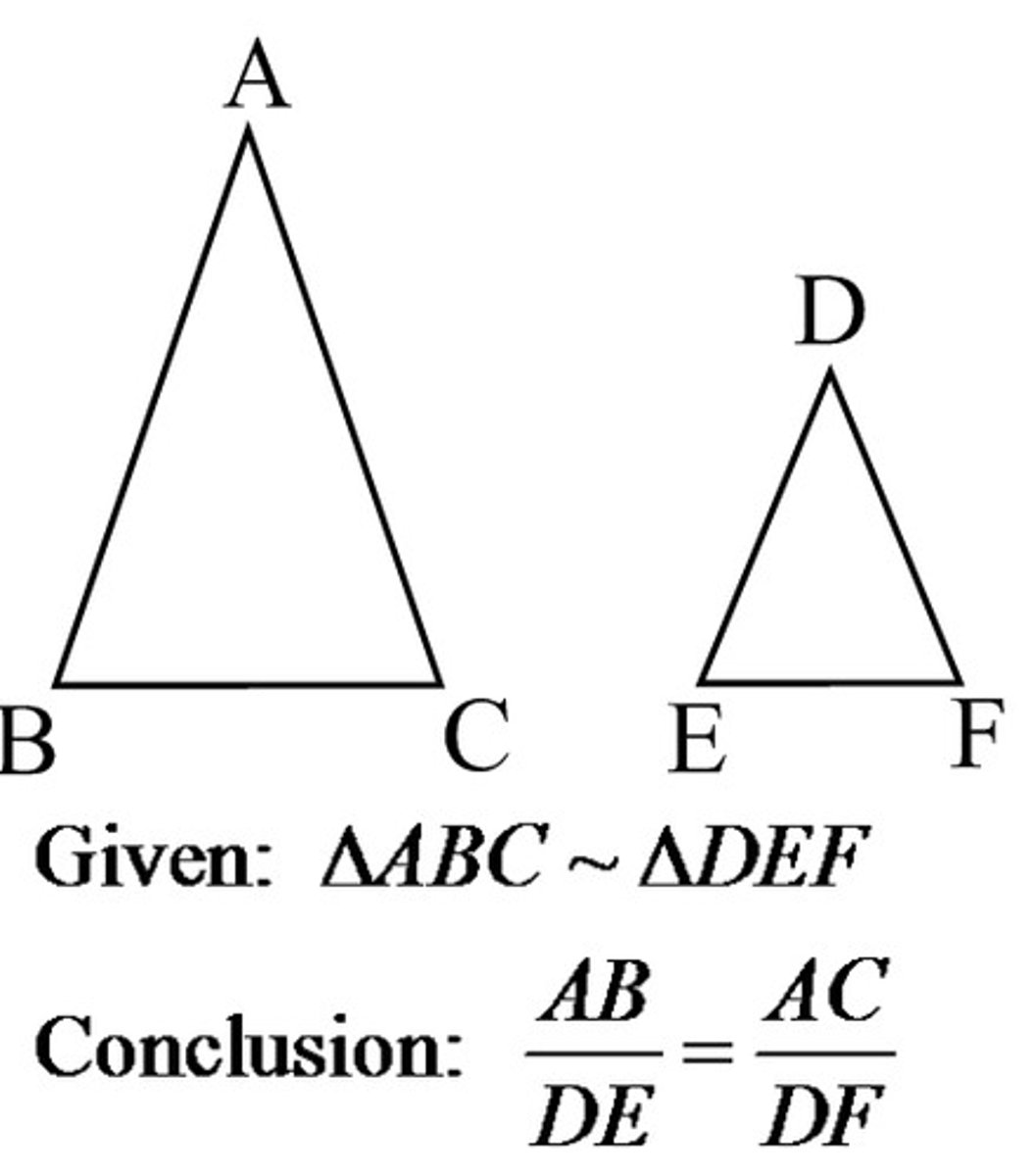
Corresponding sides of similar triangles are ____?

Proportional

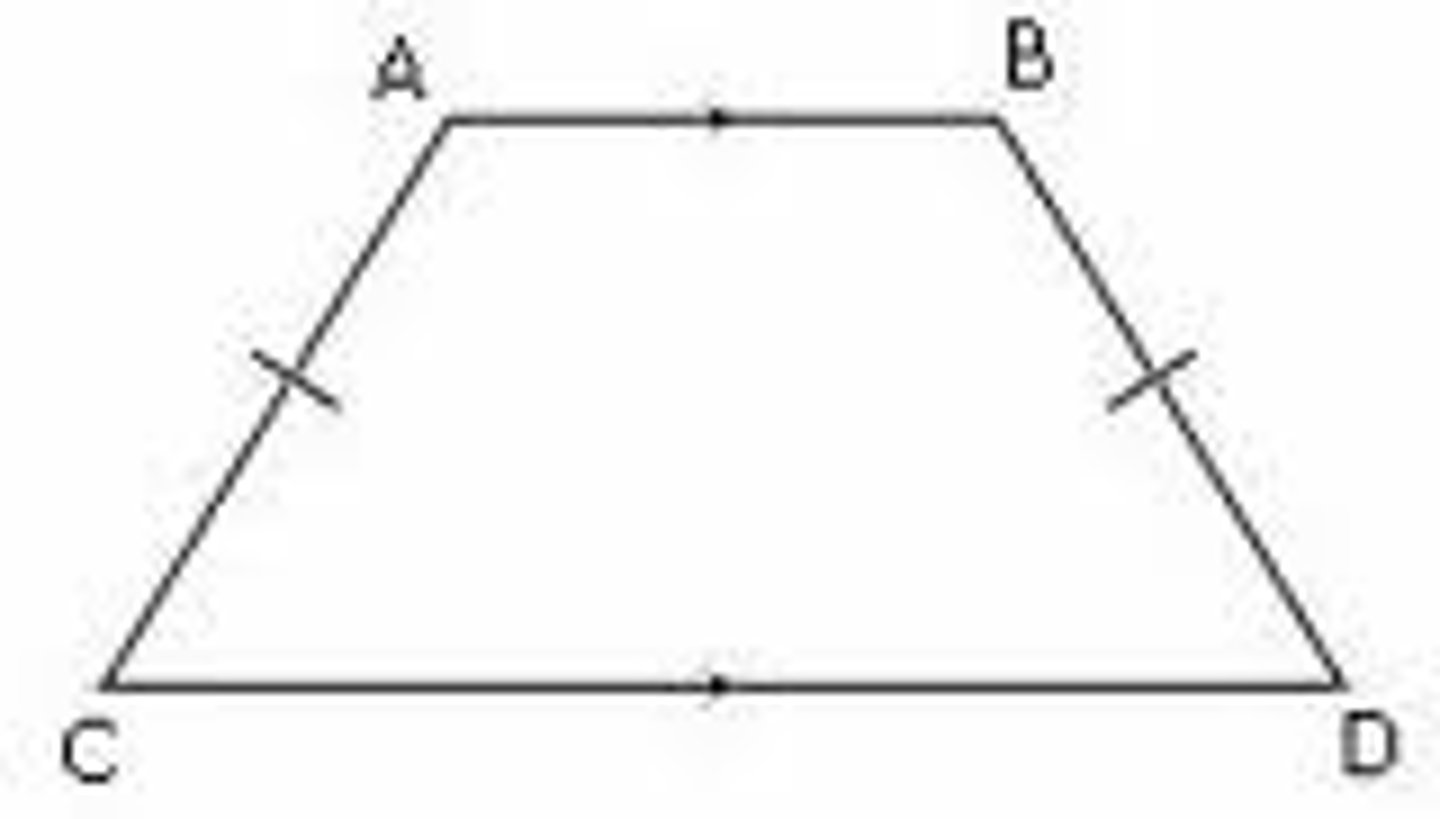
Legs in an isosceles trapezoid are

Congruent

if 2 parallel lines are cut by a transversal the alternate angles are ___?

Congruent

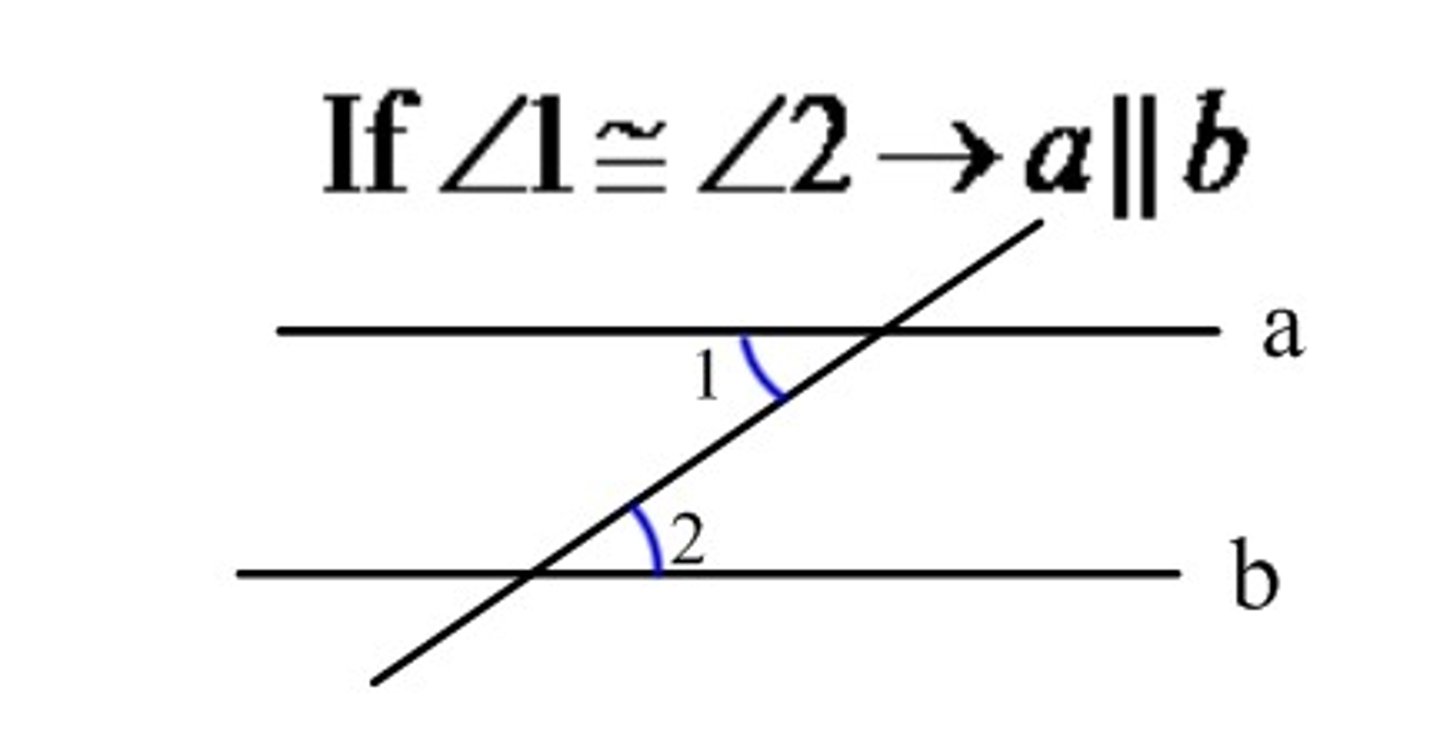
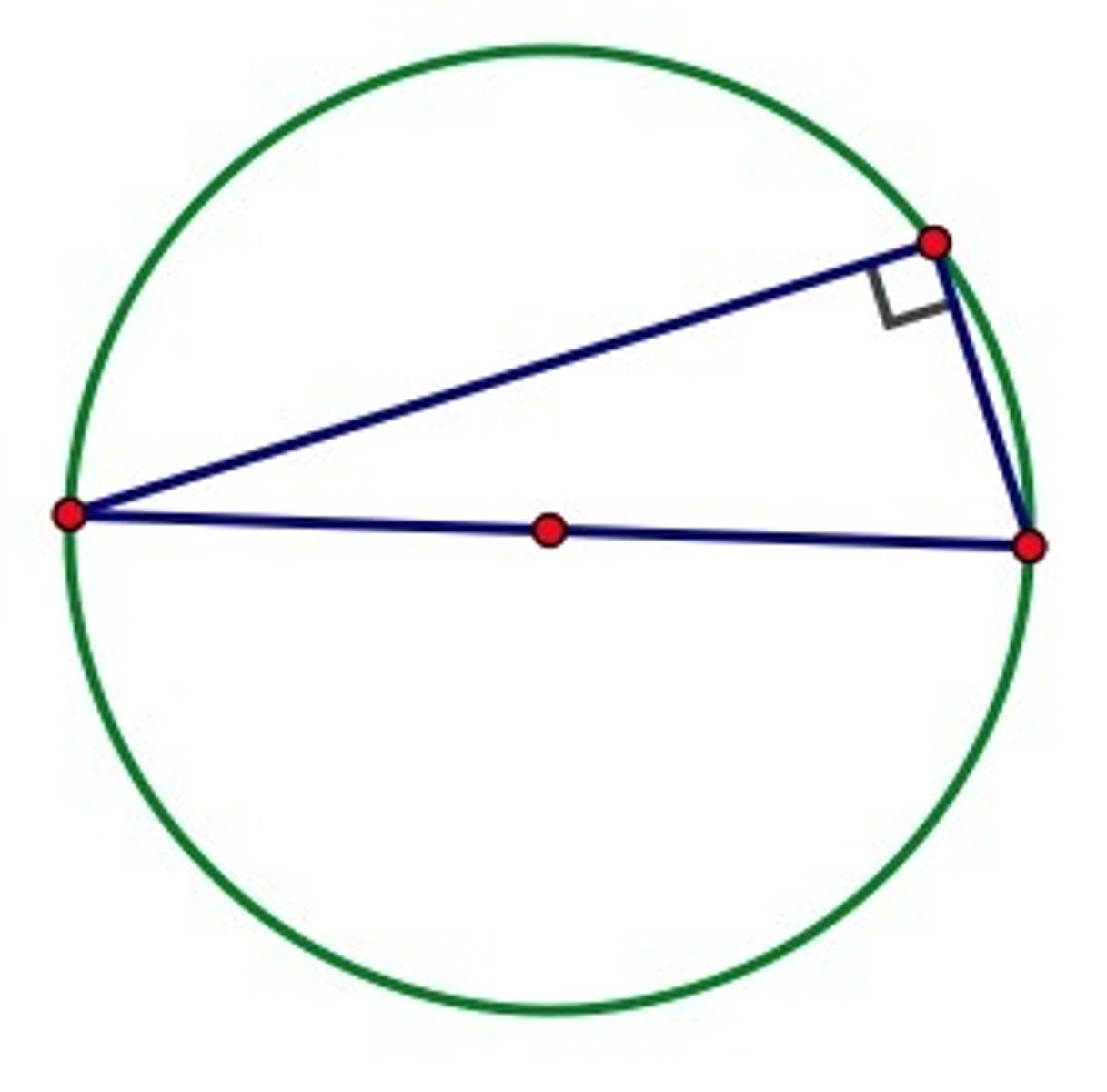
Skip (Need Therum to add)

Is a right angle.

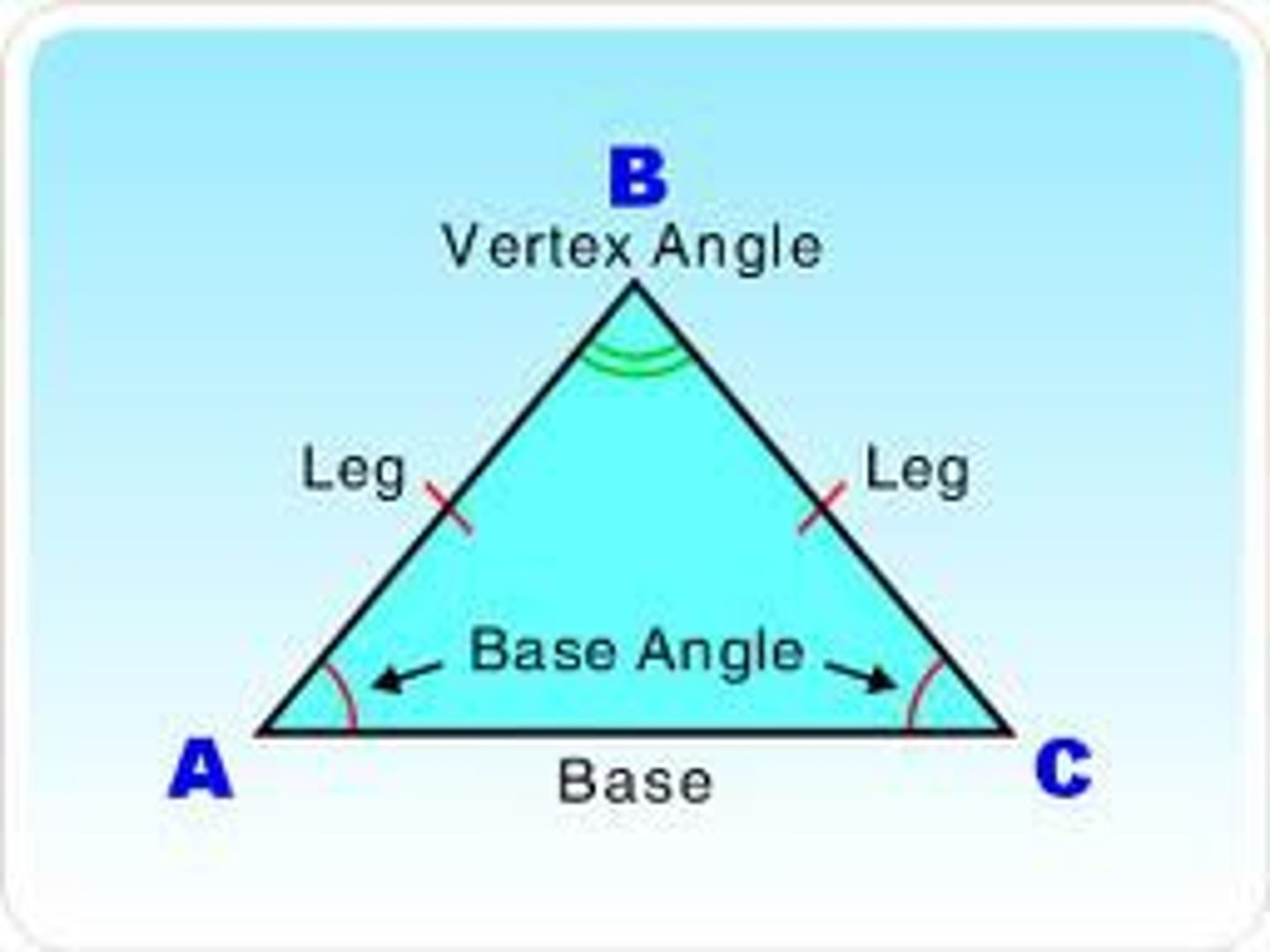
Base angles of any isosceles shape are ___?

Are congruent.

What are complementary angles?

Angles that add up to 90 degrees.

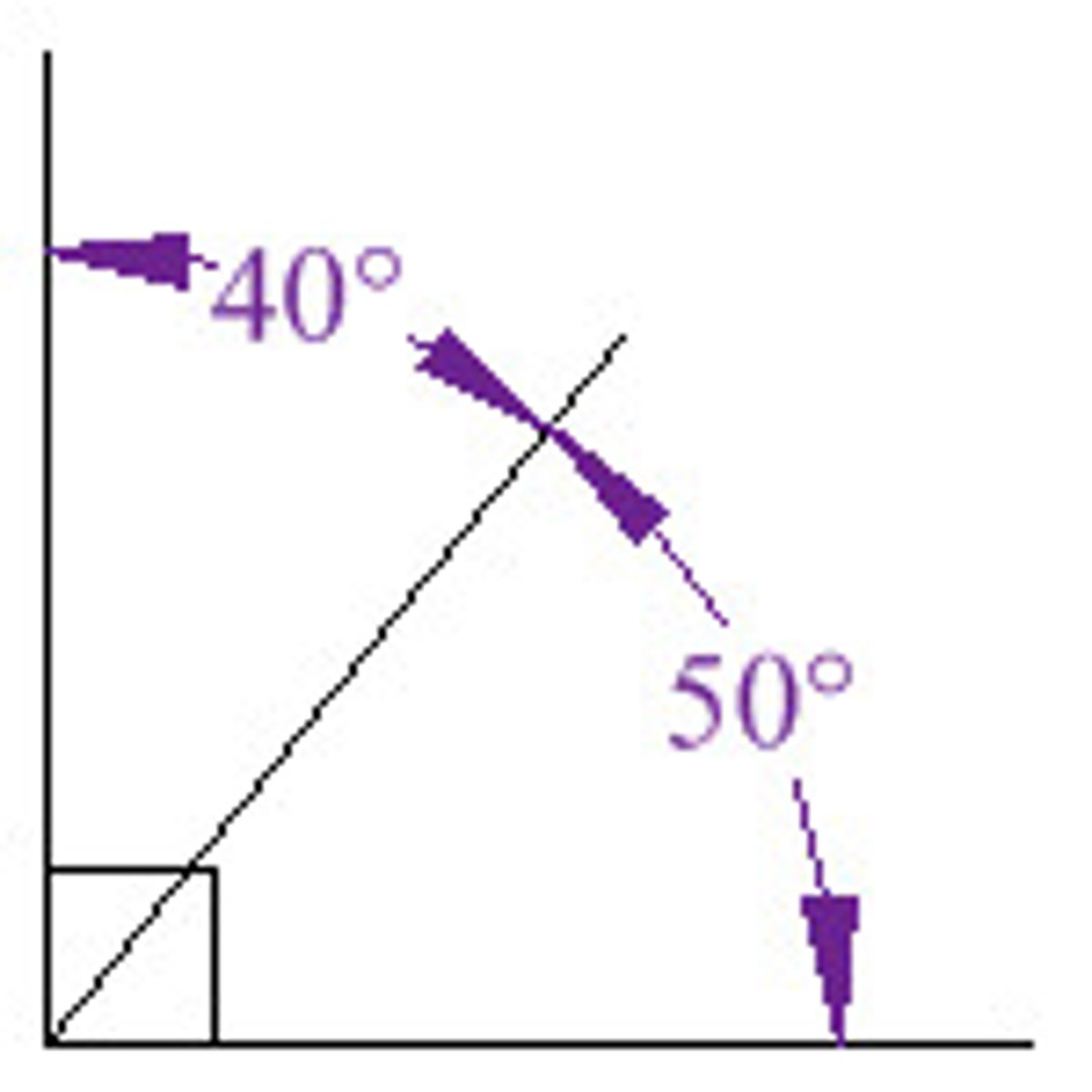
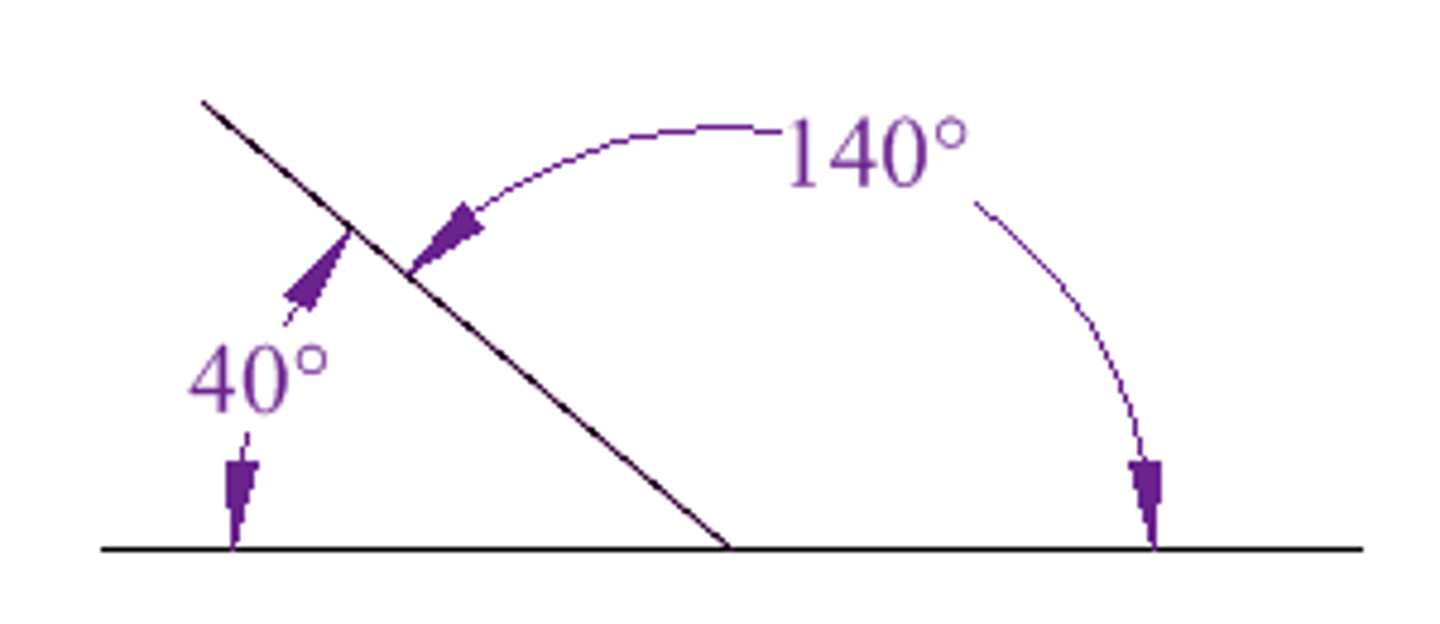
What are supplementary angles?

Angles that add up to 180.

Inscribed angles in circles are always half of what?

Of their arc

Central angles are always equal to their what in circles?

To the arc they intercept

Altitude

A line drawn from a vertex to the opposite side and is perpendicular to that side.

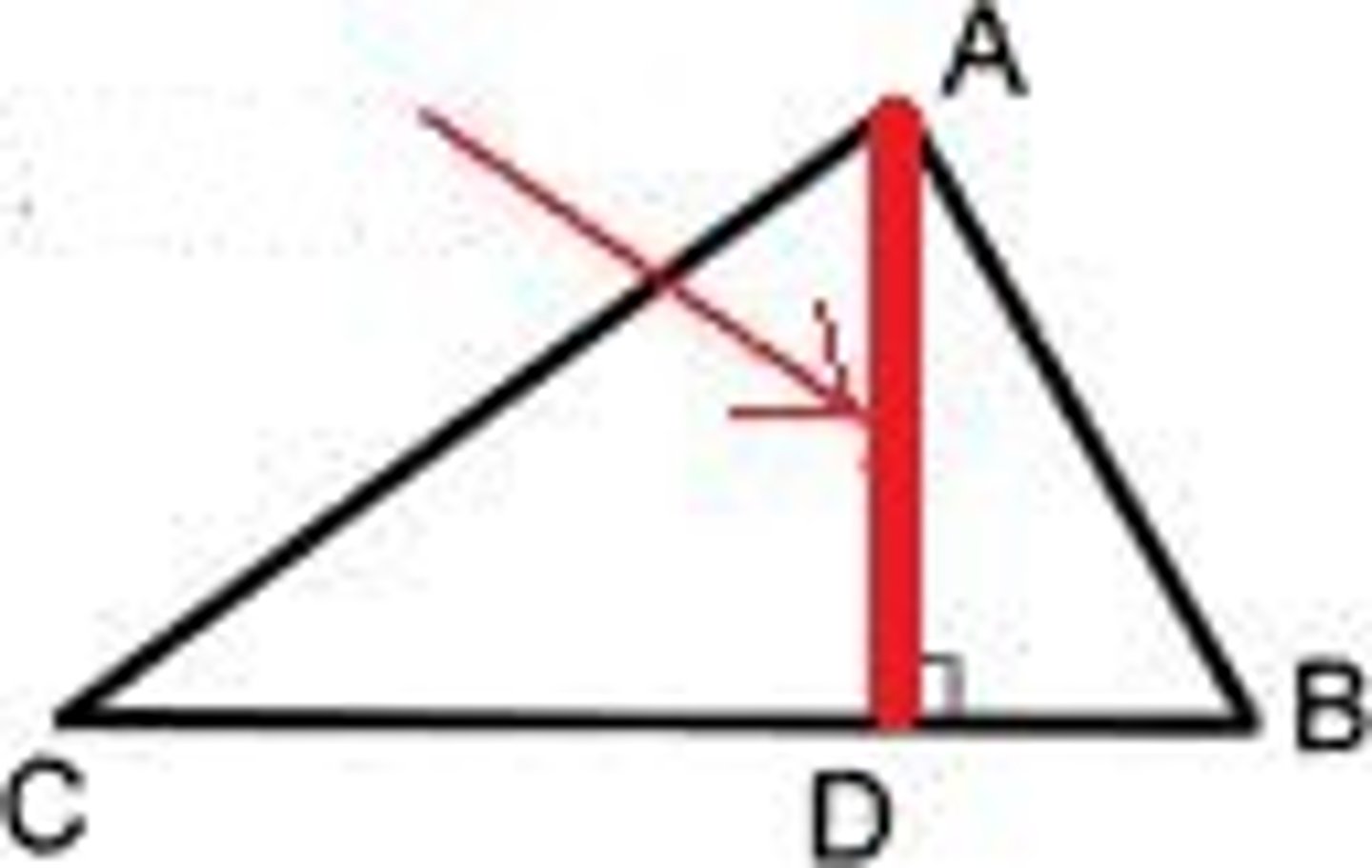
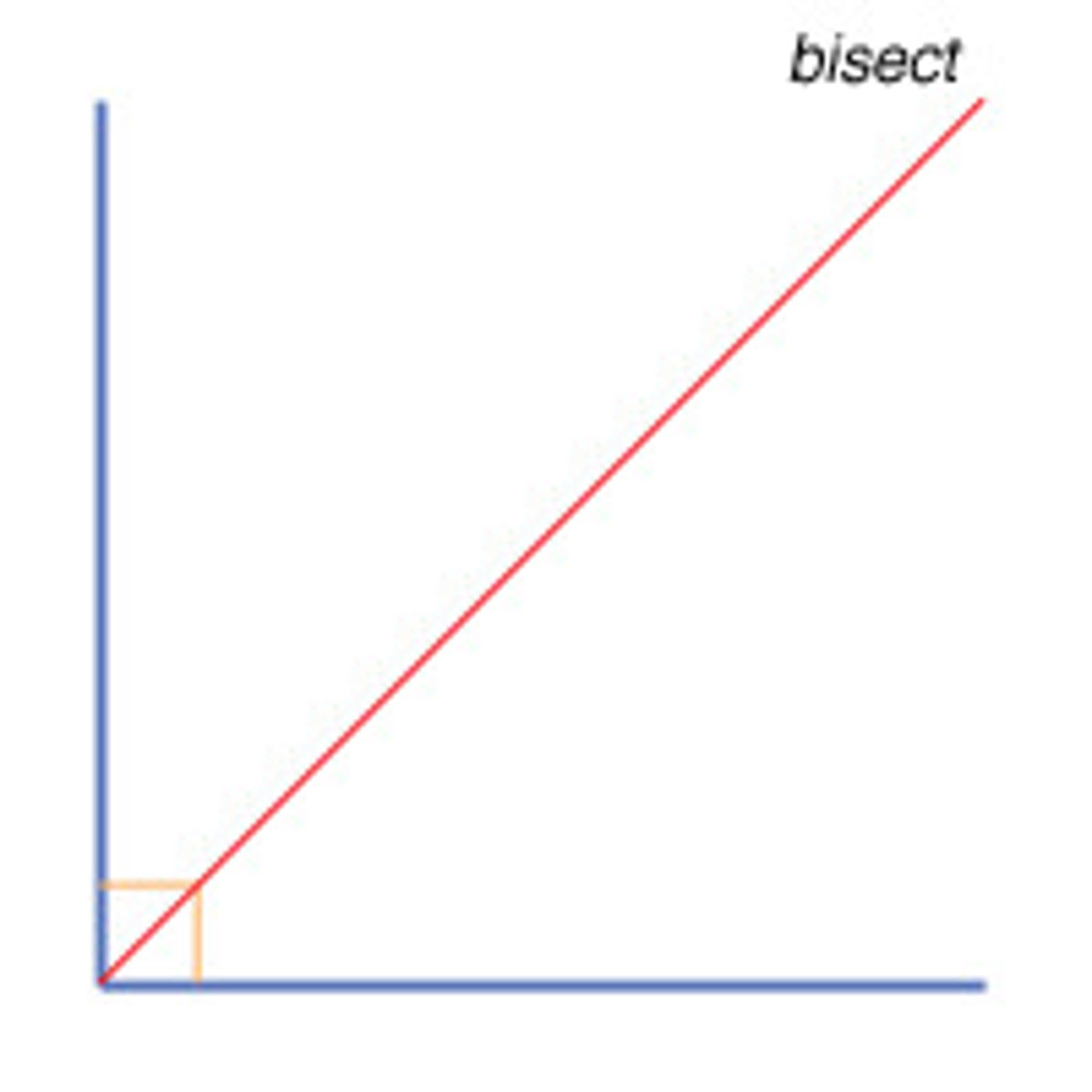
Bisector

Divide (a line, angle, shape, etc.) into two equal parts.

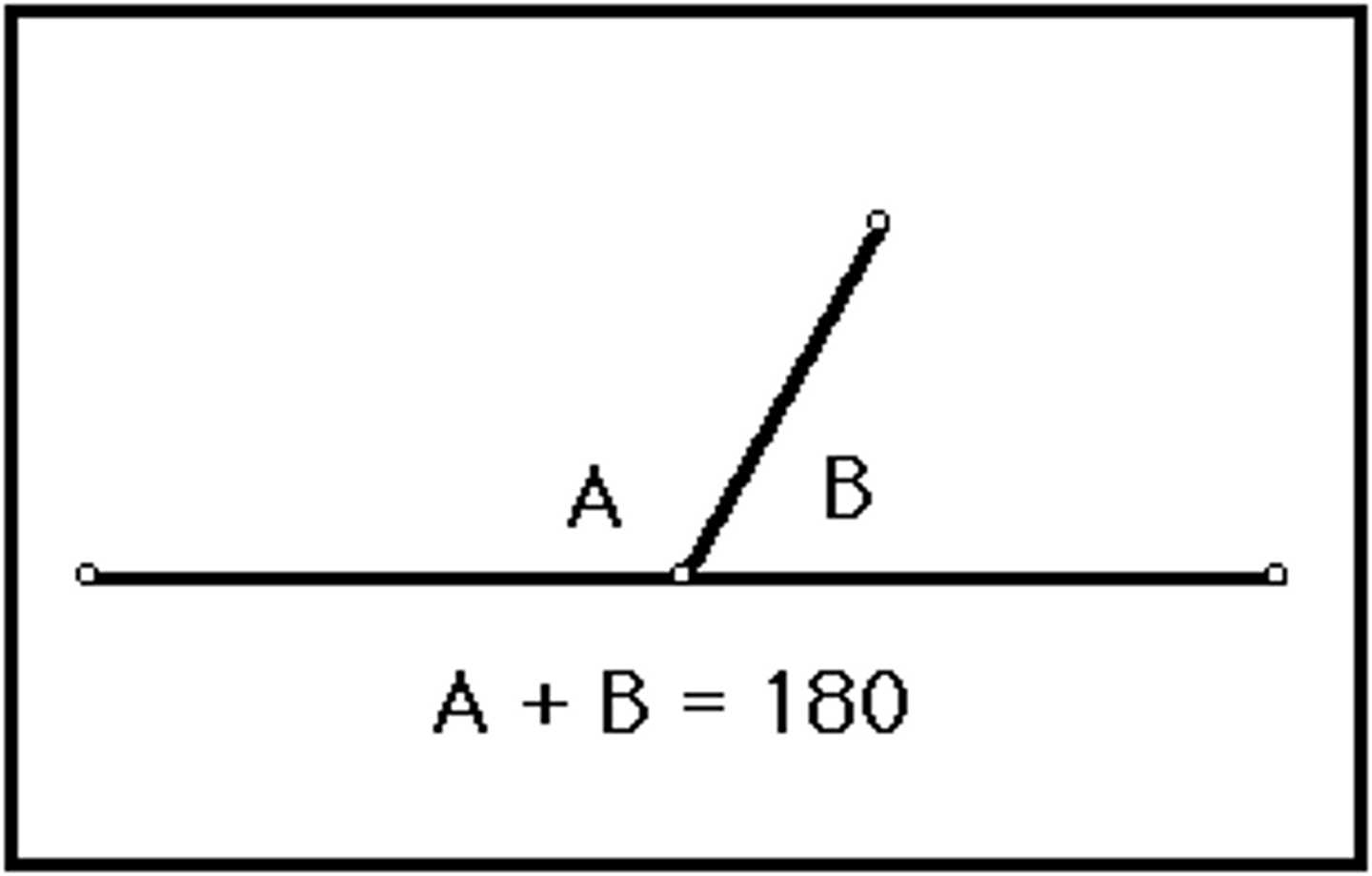
Linear pair

Two adjacent angles that form a straight line (180º line)

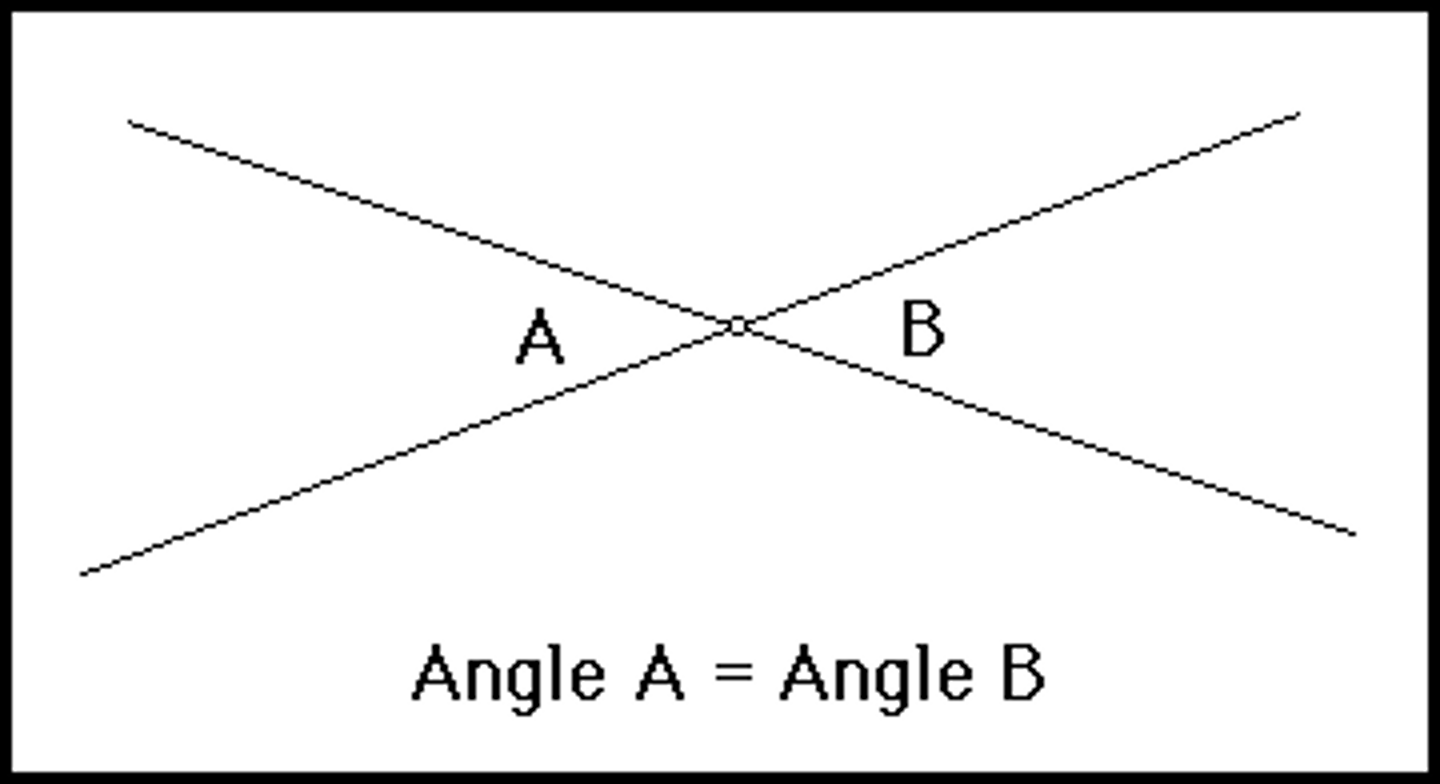
Vertical angles

The congruent opposite angles formed by intersecting lines

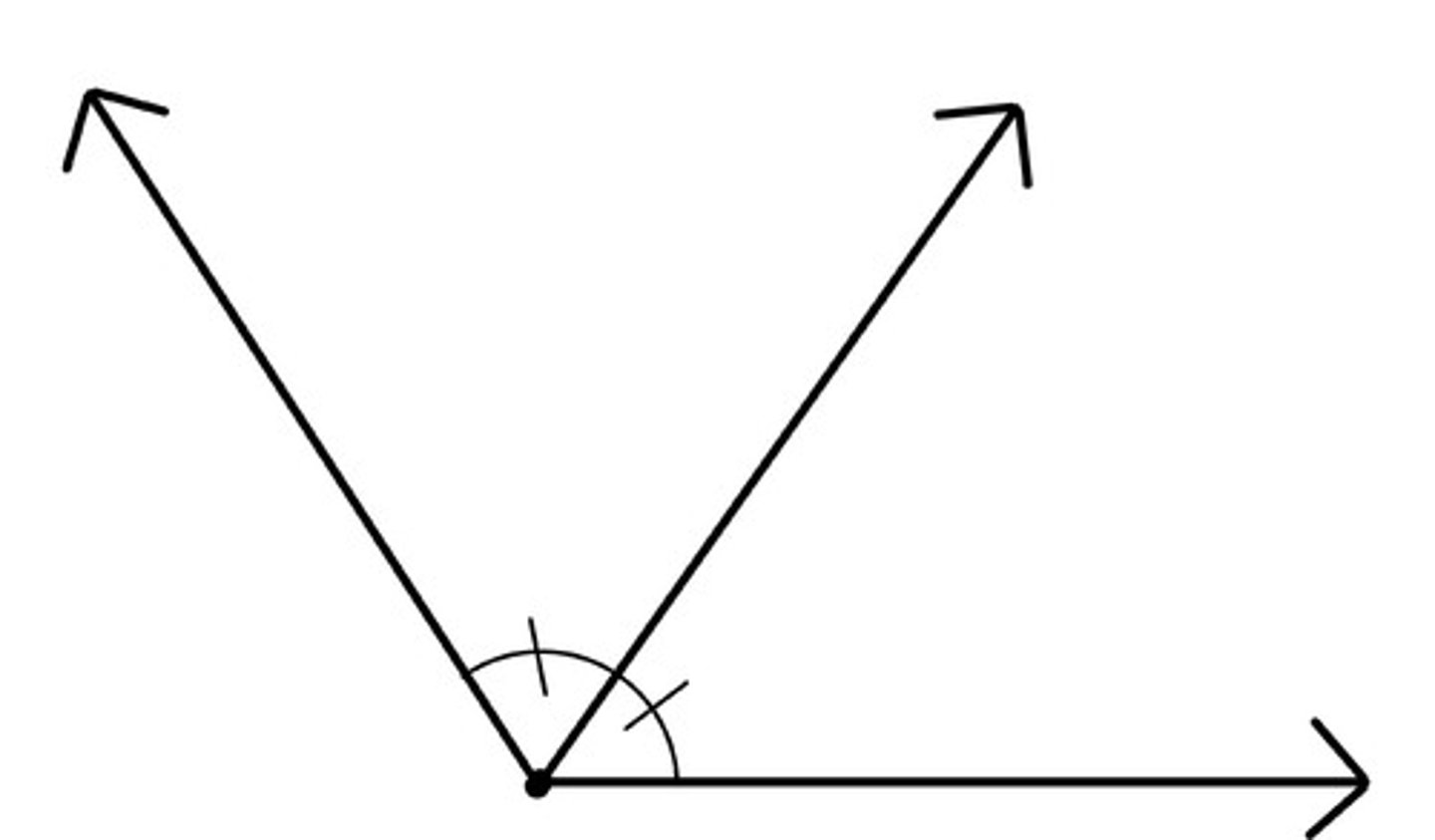
Angle bisectors

Divide angles into two congruent angles.

Alternate interior angles are ___?

Are congruent.

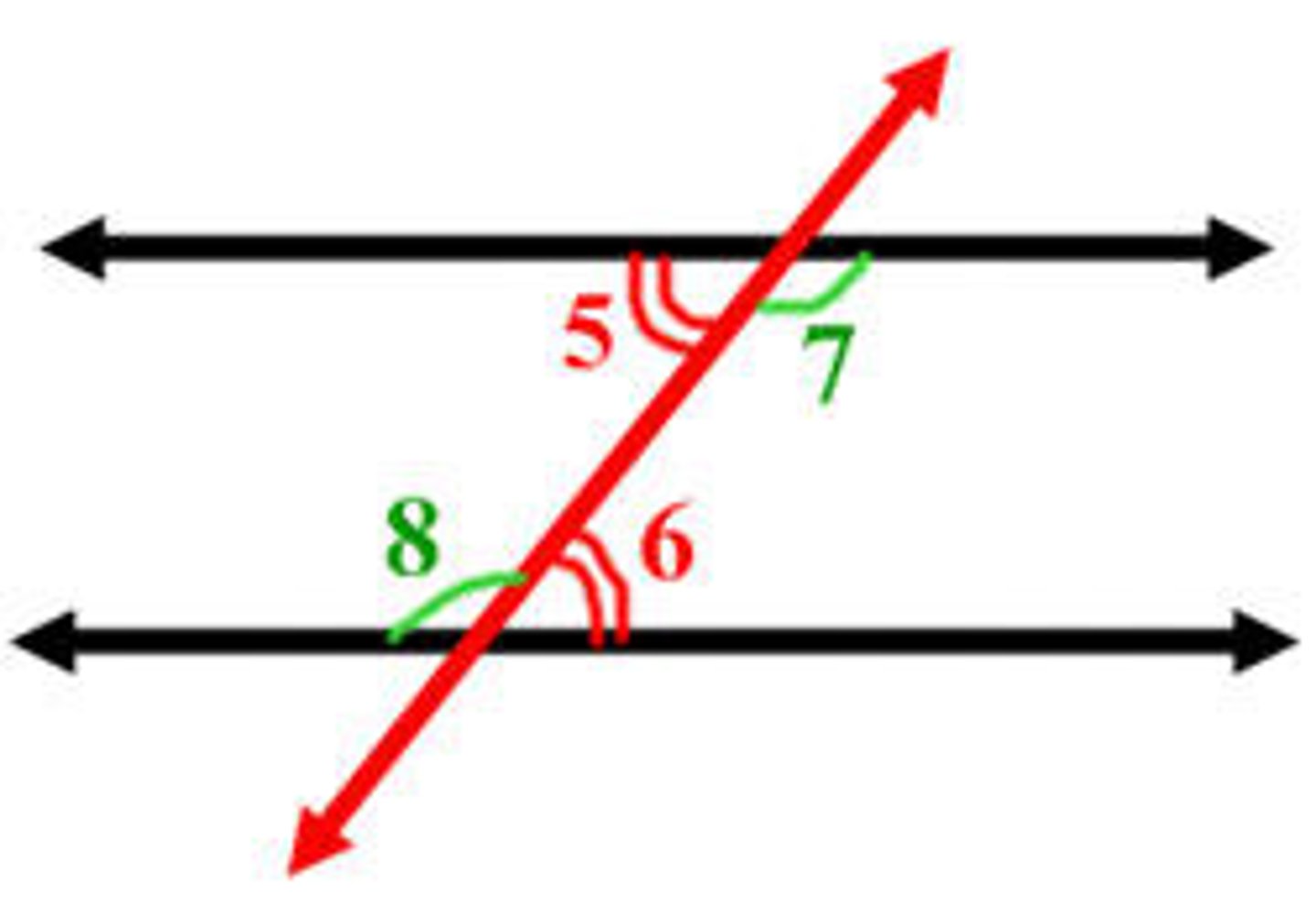
Same side interior angles are ___?

Are supplementary.

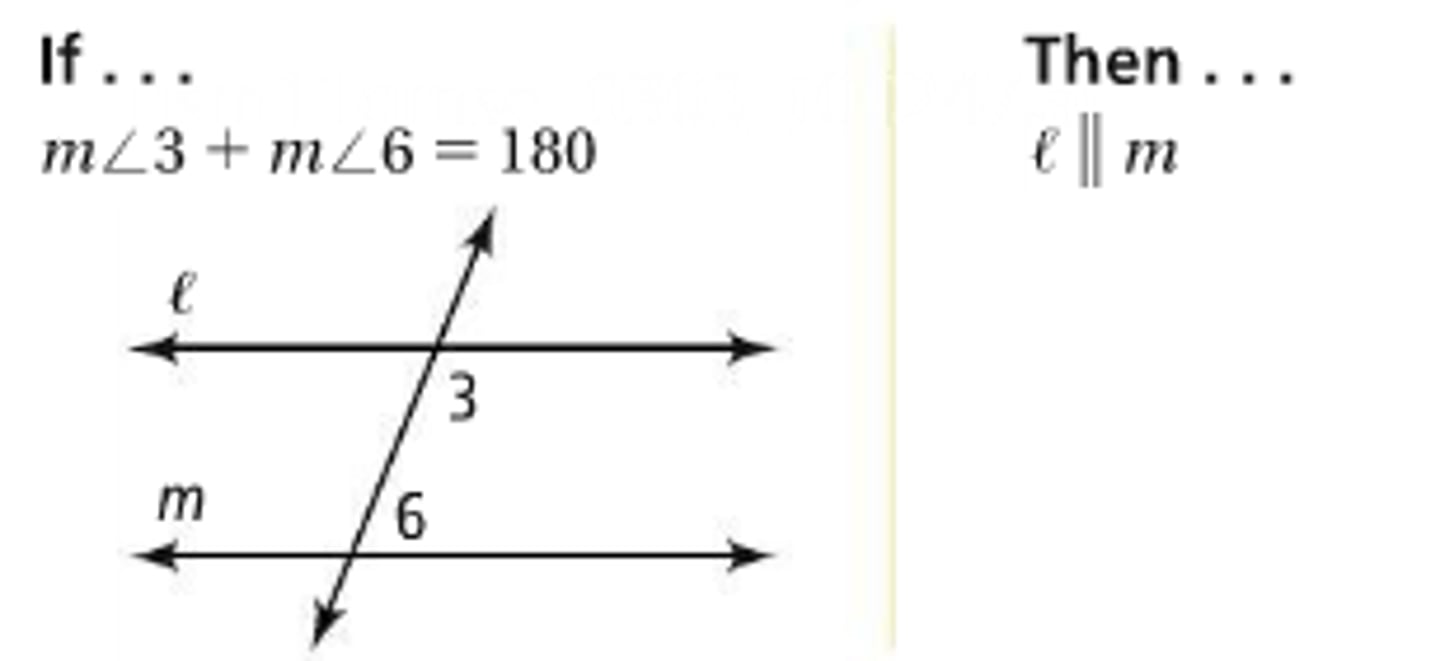
Corresponding angles are ___?

Are congruent.

Perpendicular bisector

A line, segment, or ray that is perpendicular to and bisects a segment.

median

A segment from the vertex to the midpoint of th opposite side. Bisects that side.

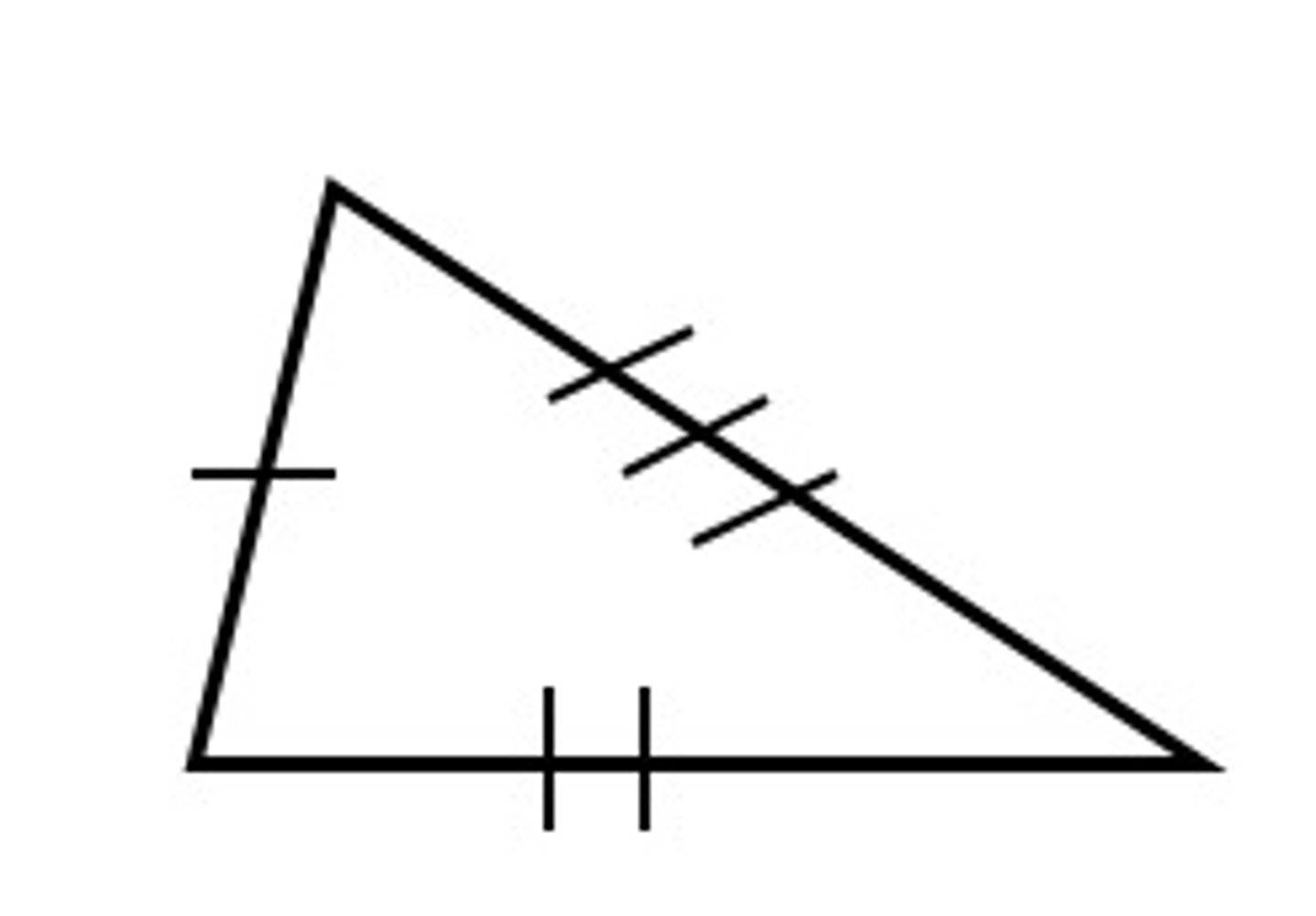
Scalene triangle

No sides are congruent

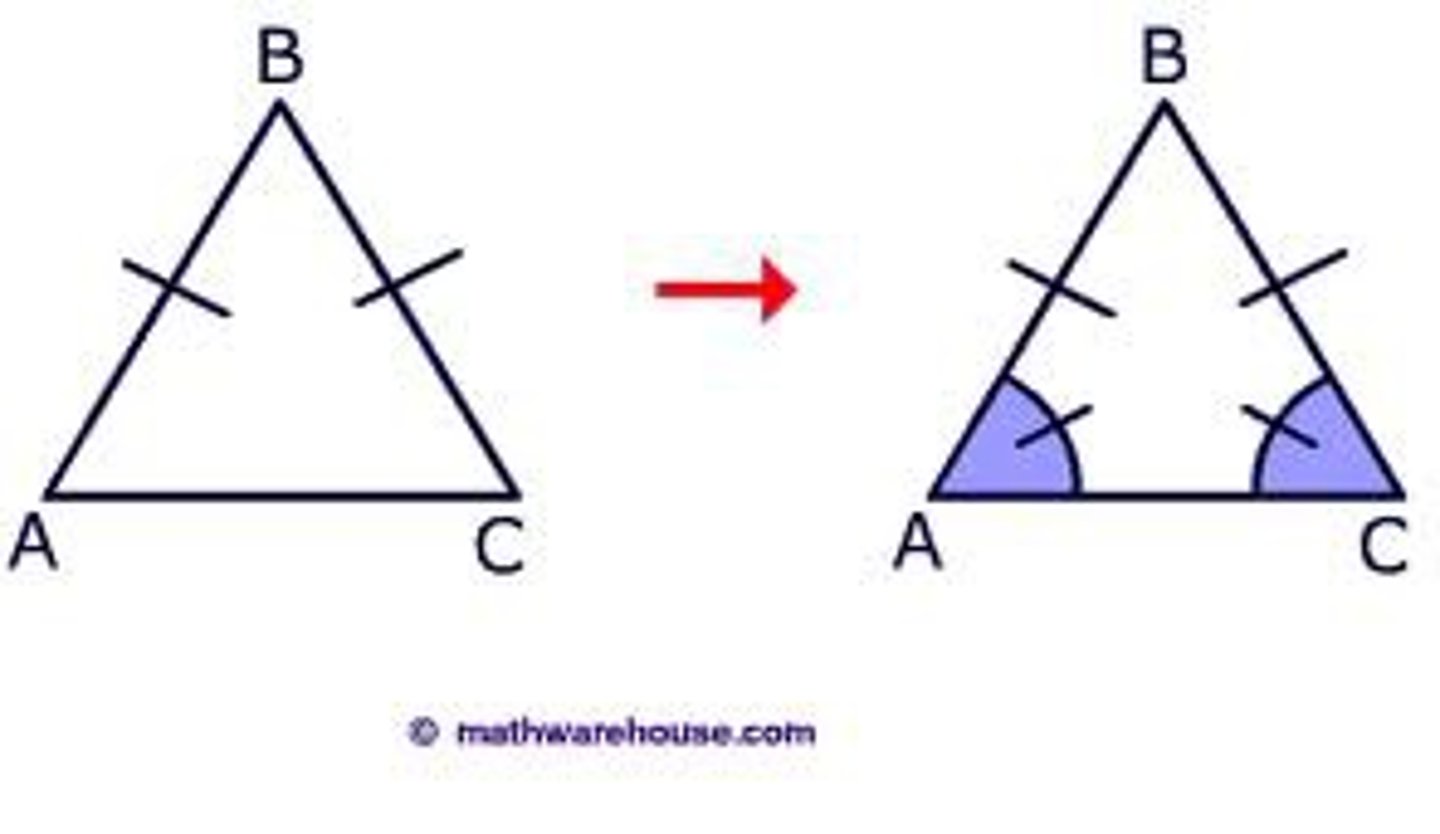
Isosceles triangle

Two legs of the triangle are congruent. Base angles are congruent

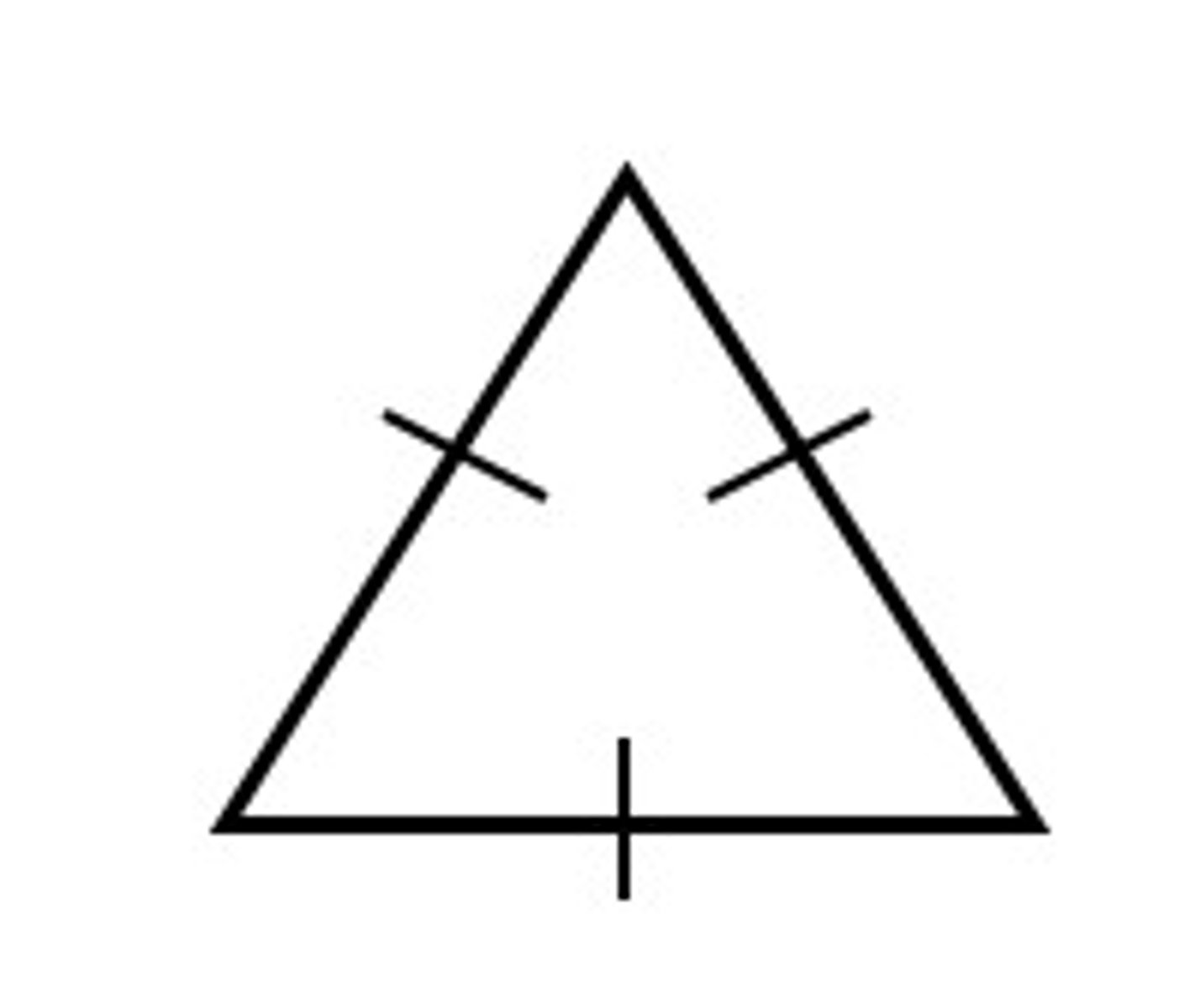
Equilateral triangle

Three sides are congruent.

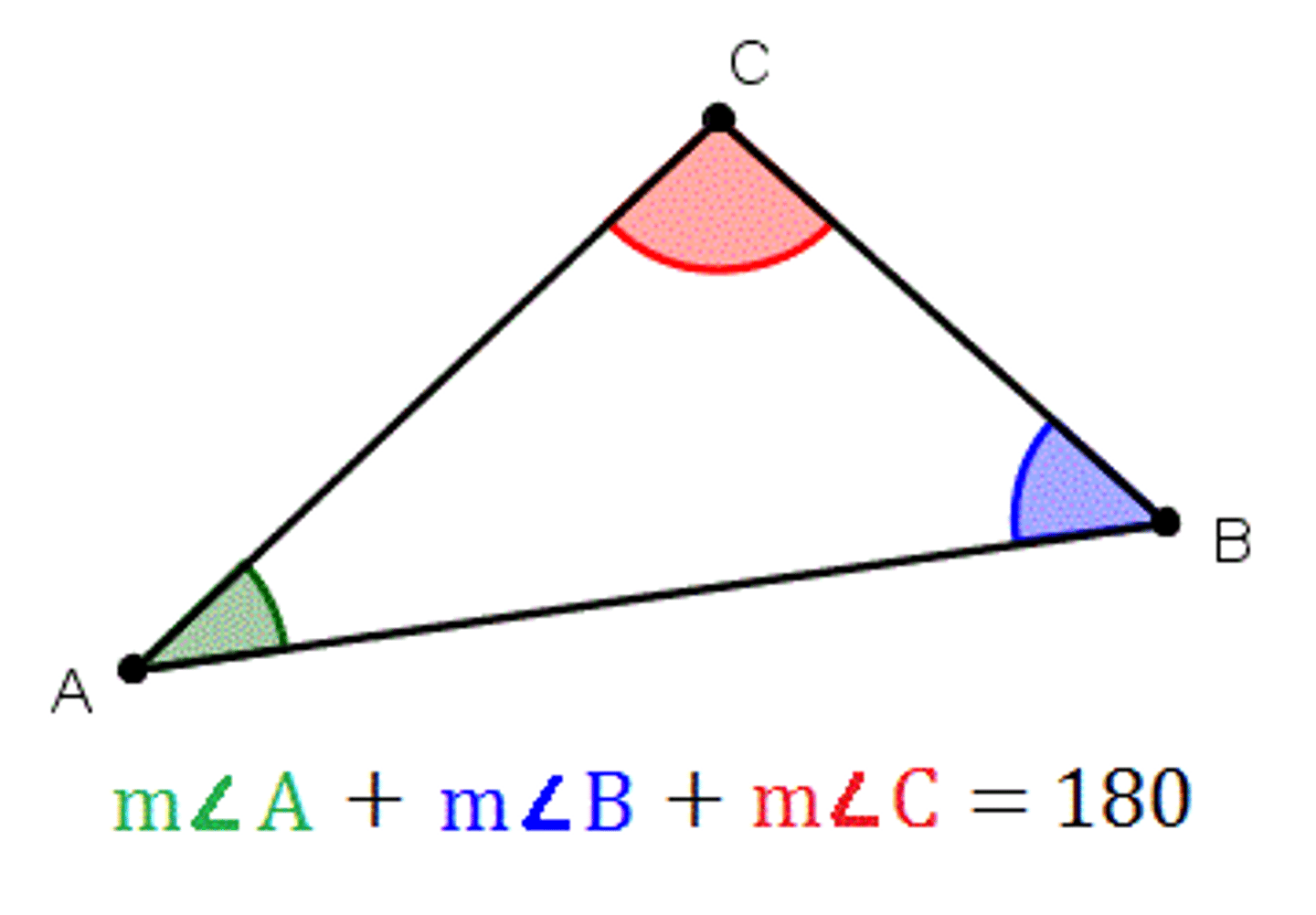
Angle sum theorem

The sum of the measures of the interior angles = 180º

Exterior angle theorem

The measure of any exterior angle of a triangle = the sum of the measures of the nonadjacent interior angles.

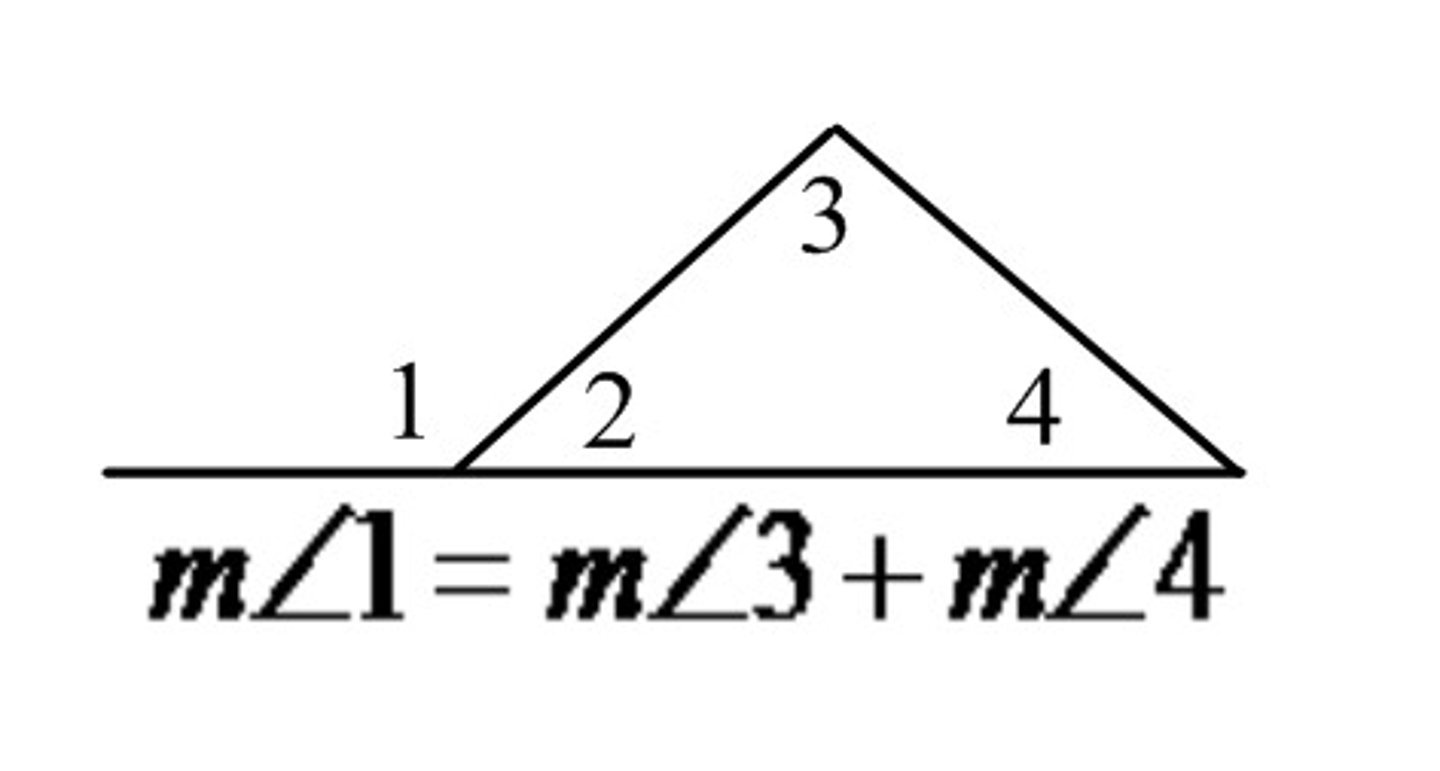
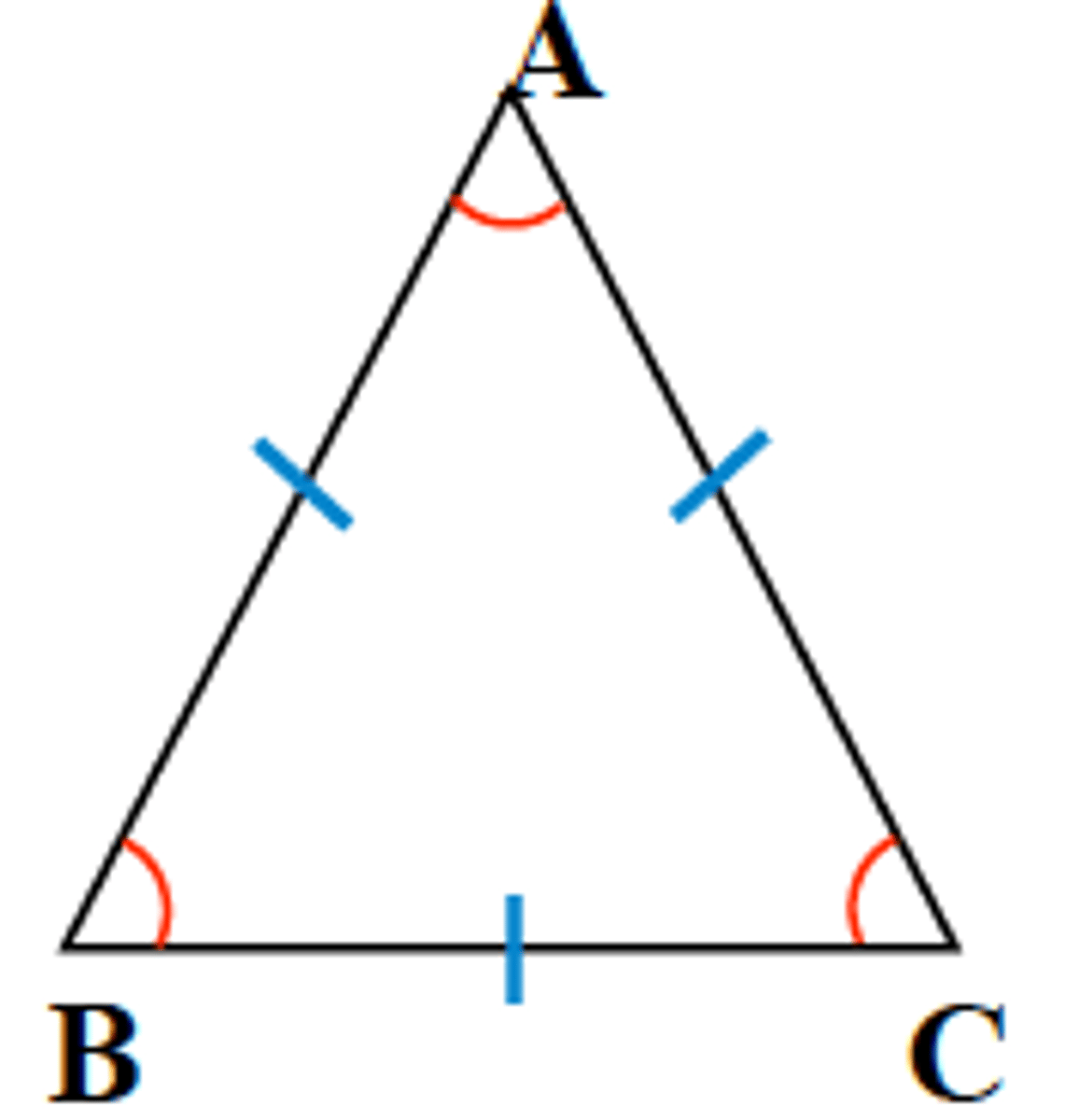
equilateral triangle theorem

all interior angles of an equilateral triangle measure 60º

Pythagorean theorem

In a right triangle, a² + b² = c².

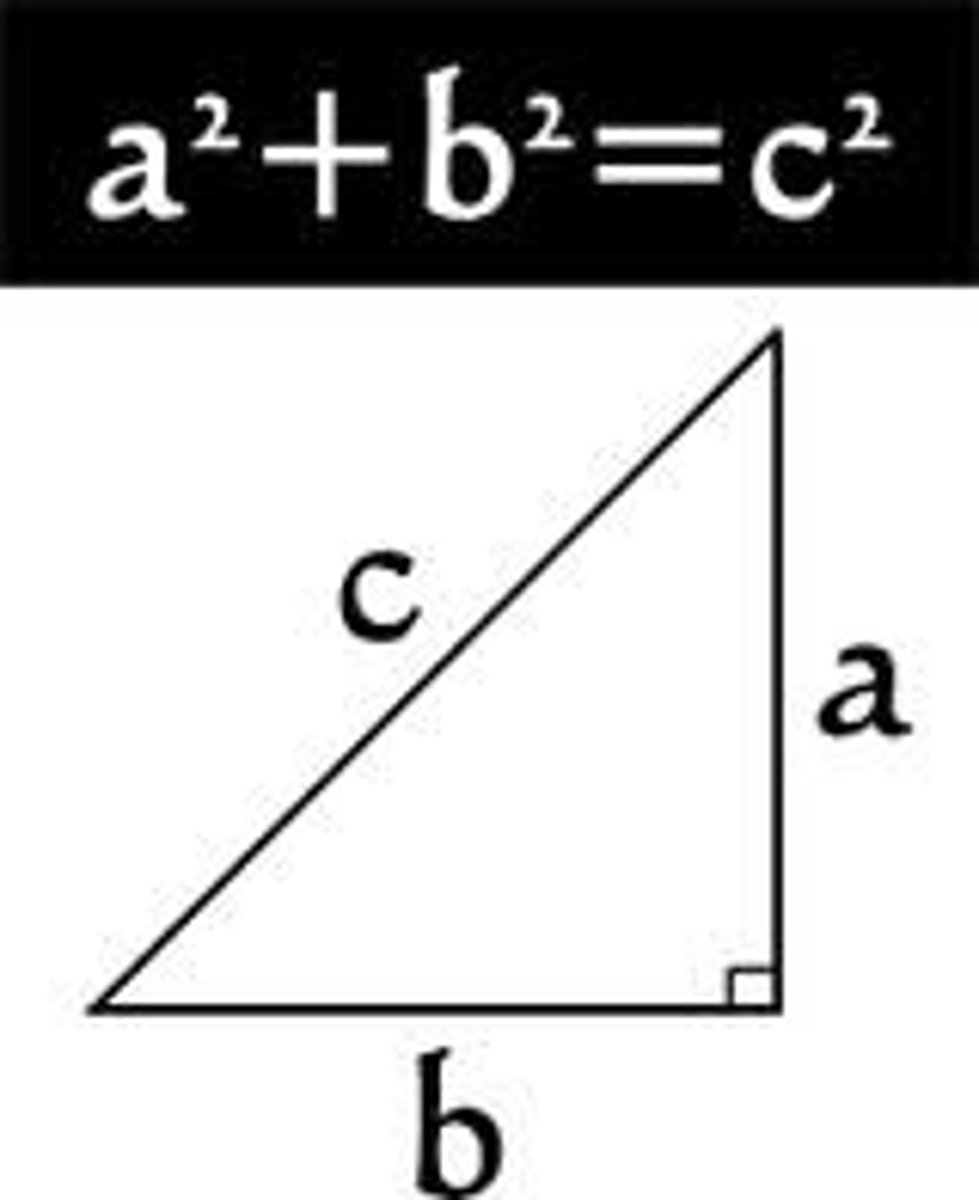
slope formula

y=mx+b

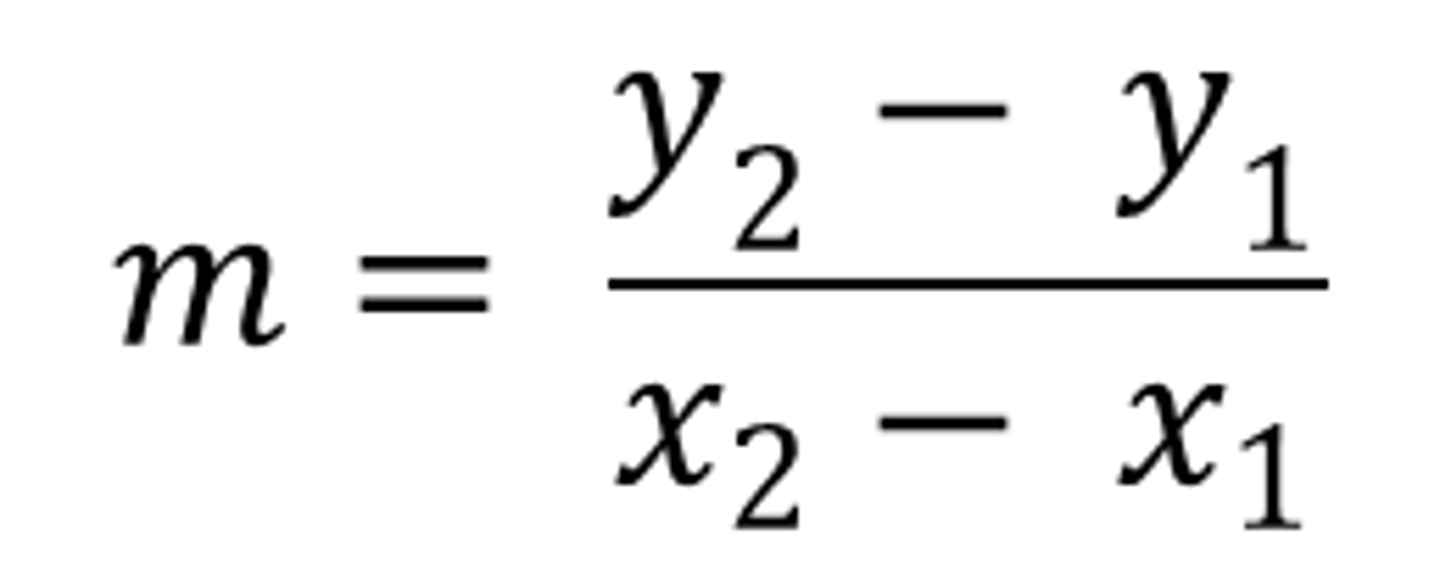
Distance formula

D = √(x₂ - x₁)squared+ (y₂ - y₁)squared

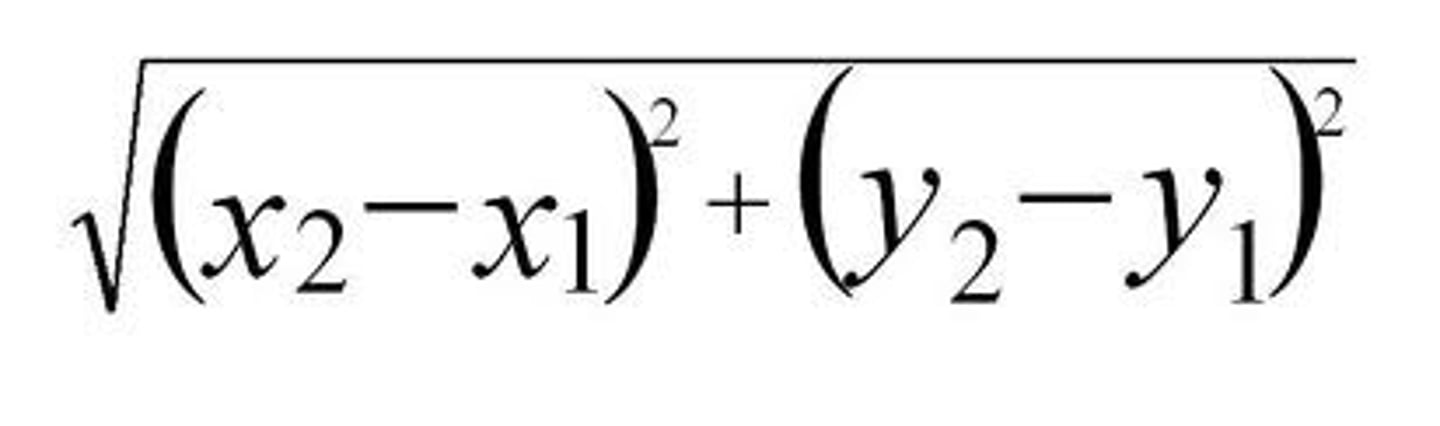
Opposite reciprocals

Two lines that slopes are opposite. They're perpendicular.

Segment parallel to a side theorem

-If a segment intersects two sides of a triangle such that a triangle similar to the OG triangle is formed, the segment is parallel to the third side

Side splitter theorem

A segment parallel to a side in a triangle divides the two sides it intersects proportionally

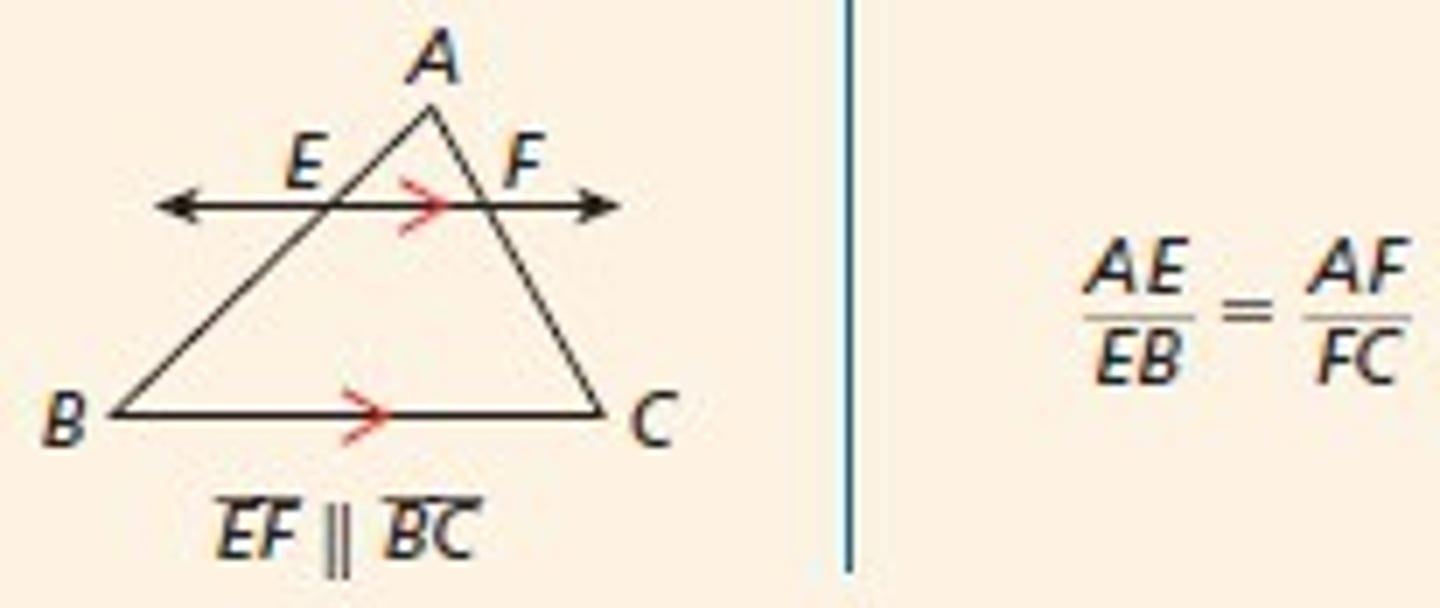
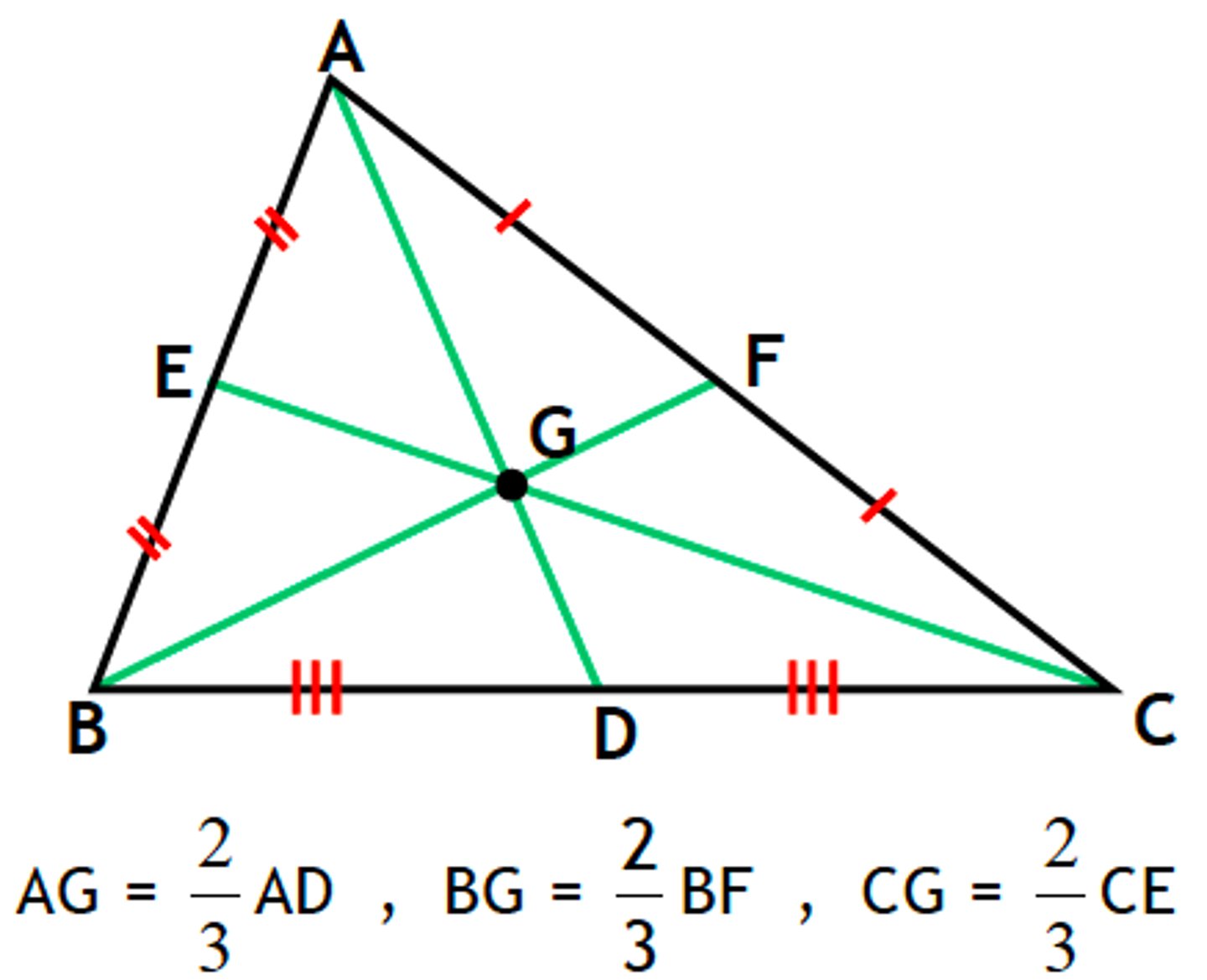
centroid theorem

the centroid of a triangle divides each median in a 1:2 ratio, with the longer segmant having a vertex as one of its endpoints

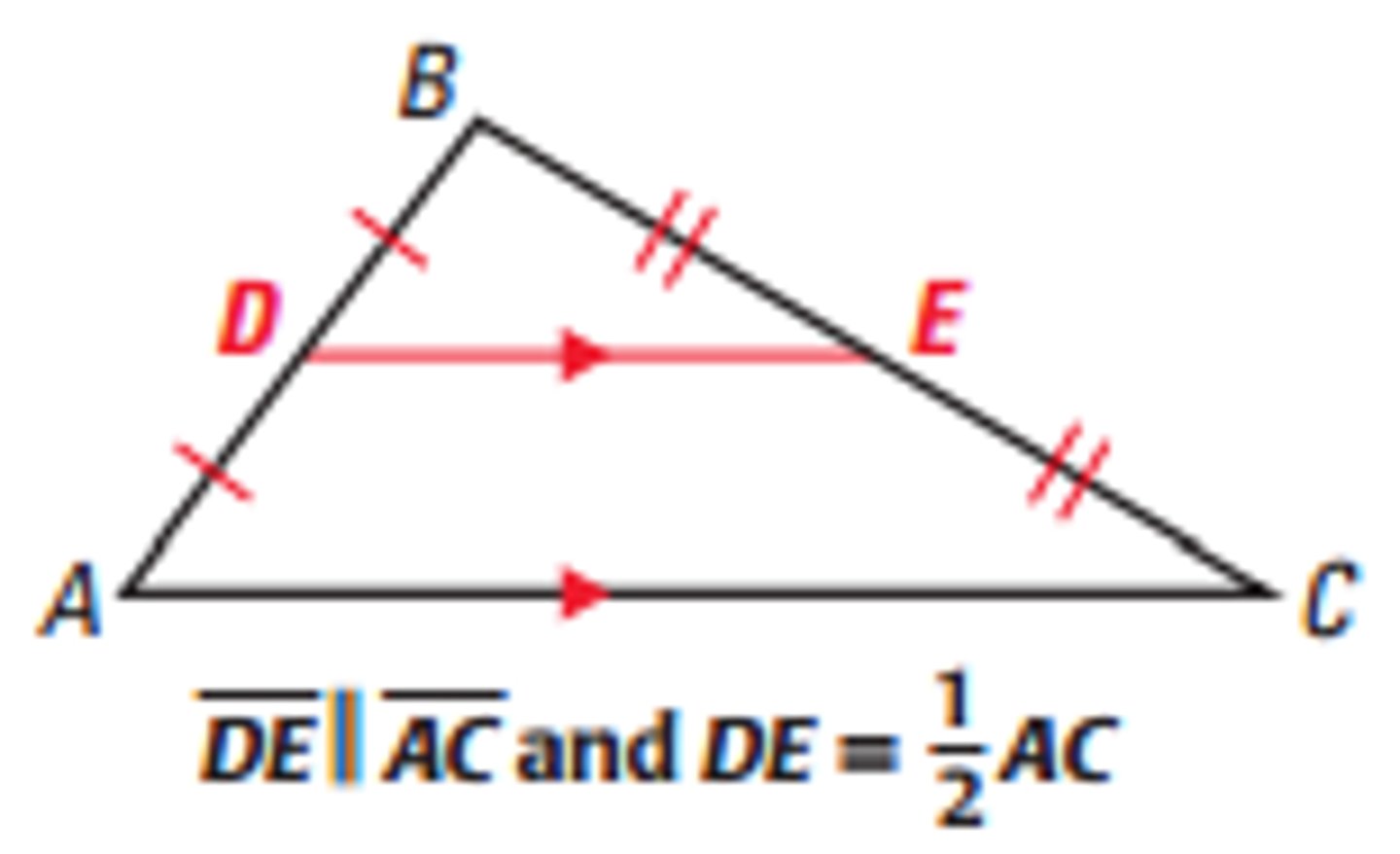
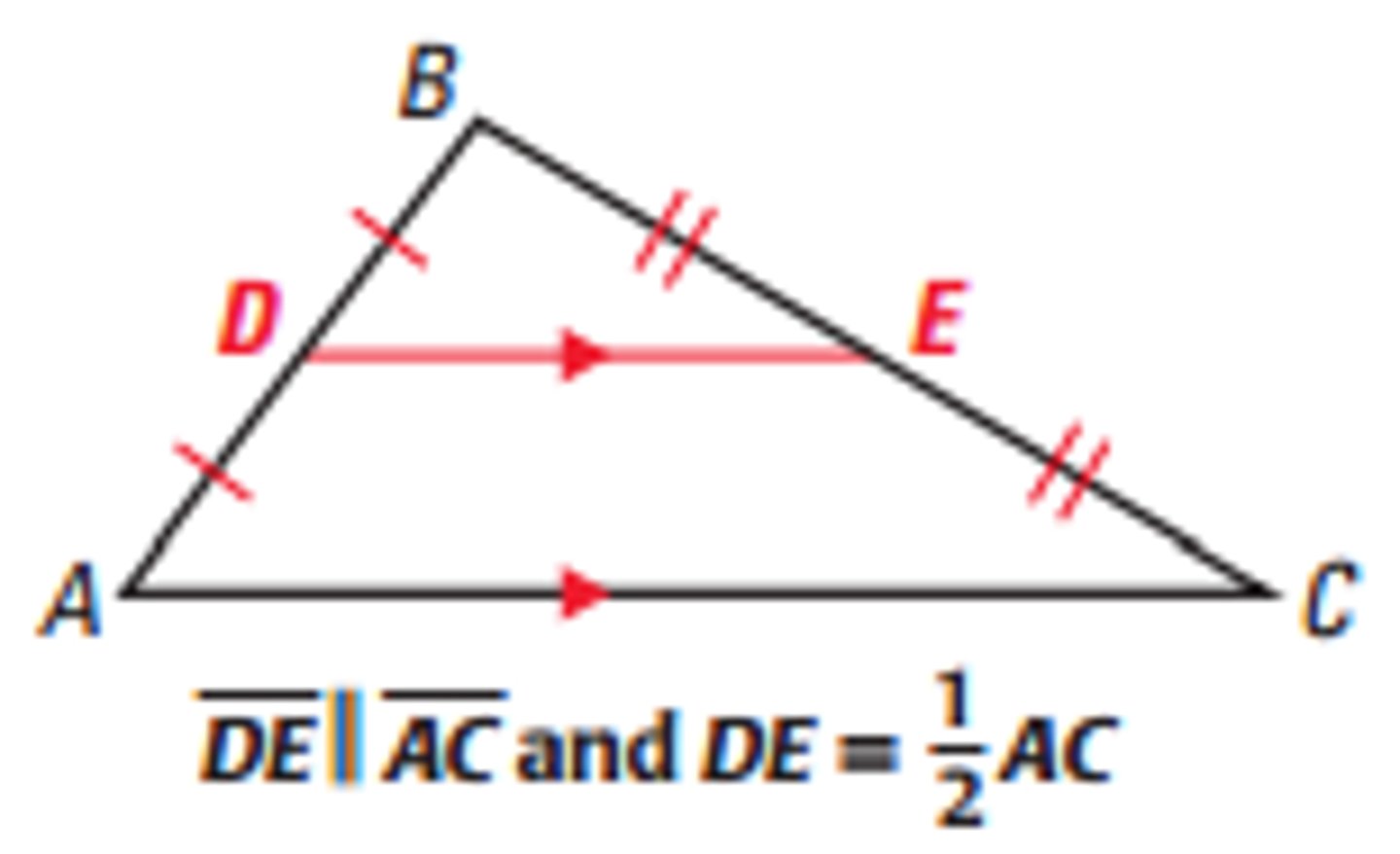
midsegment theorem

a segment joining the midpoints of two sides of a triangle (a midsegmant) is parallel to the opposite side, and it's length is equal to 1/2 the length of the opposite side

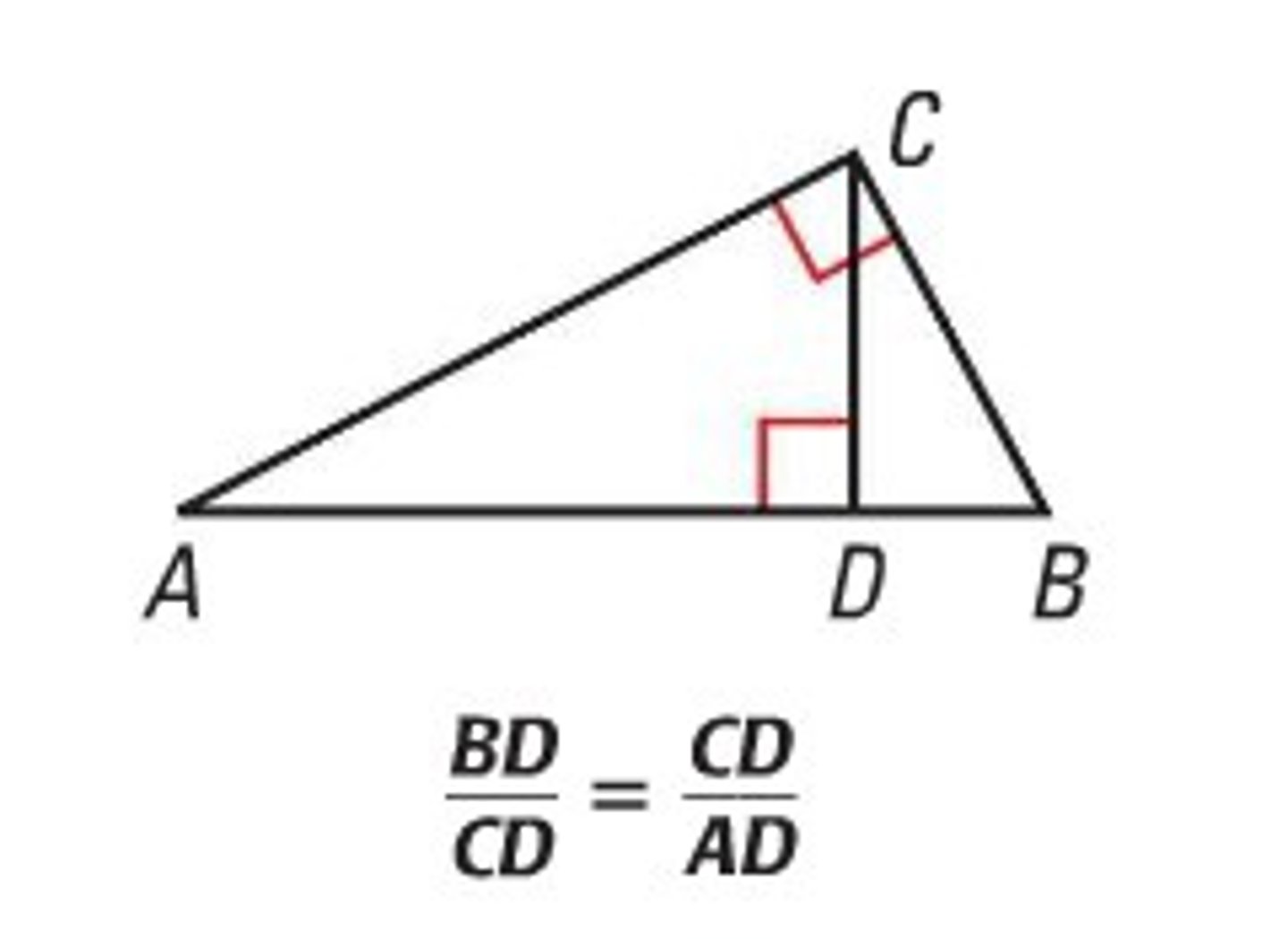
altitude to the hypotenuse of a right triangle theorem

the altitude to the hypotenuse of a right triangle forms two triangles that are similar to the O.G. triangle

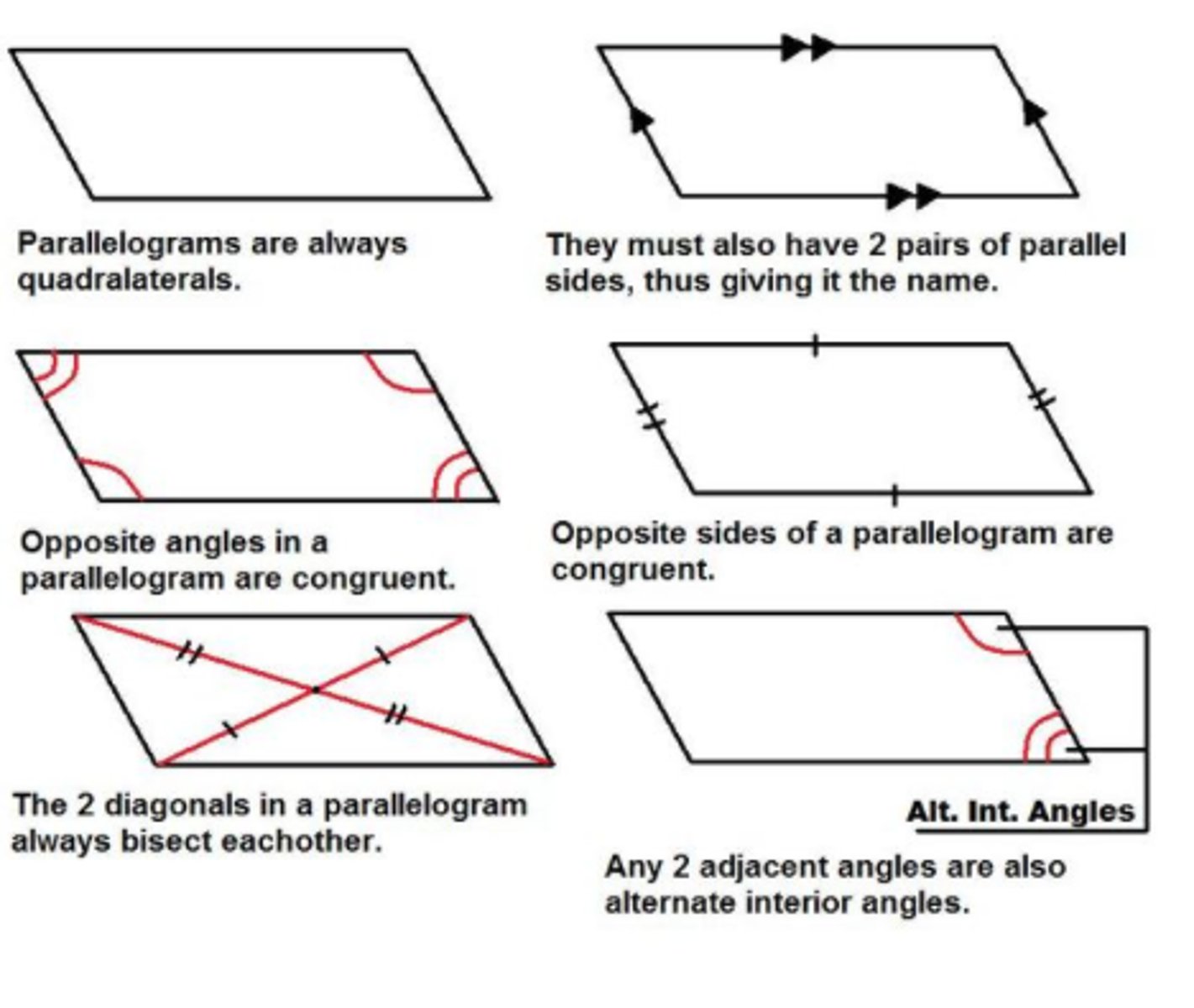
parallelogram properties

Opposite sides are parallel and =. Opposite angles are congruent. adjacent angles are supplementary. The diagonals bisect each other.diagonals divide the parallelogram into two = triangle

trapezoid properties

one pair of parallel sides. Each lower base angle is supplementary to the upper base angle on the same side.

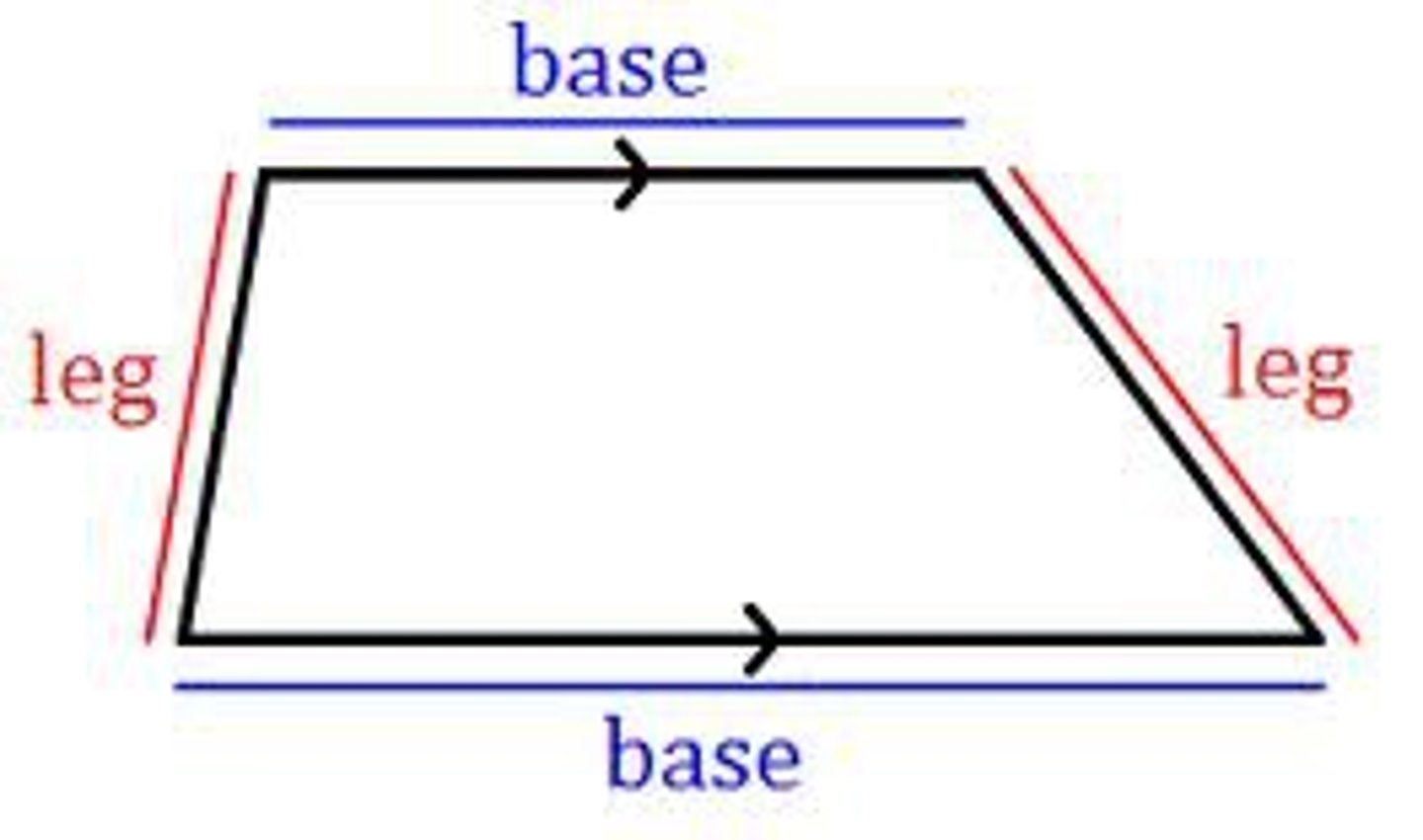
isosceles trapezoid properties

legs congruent, lower and upper base angles congruent, Any lower base angle is supplementary to any upper base angle, diagonals congruent

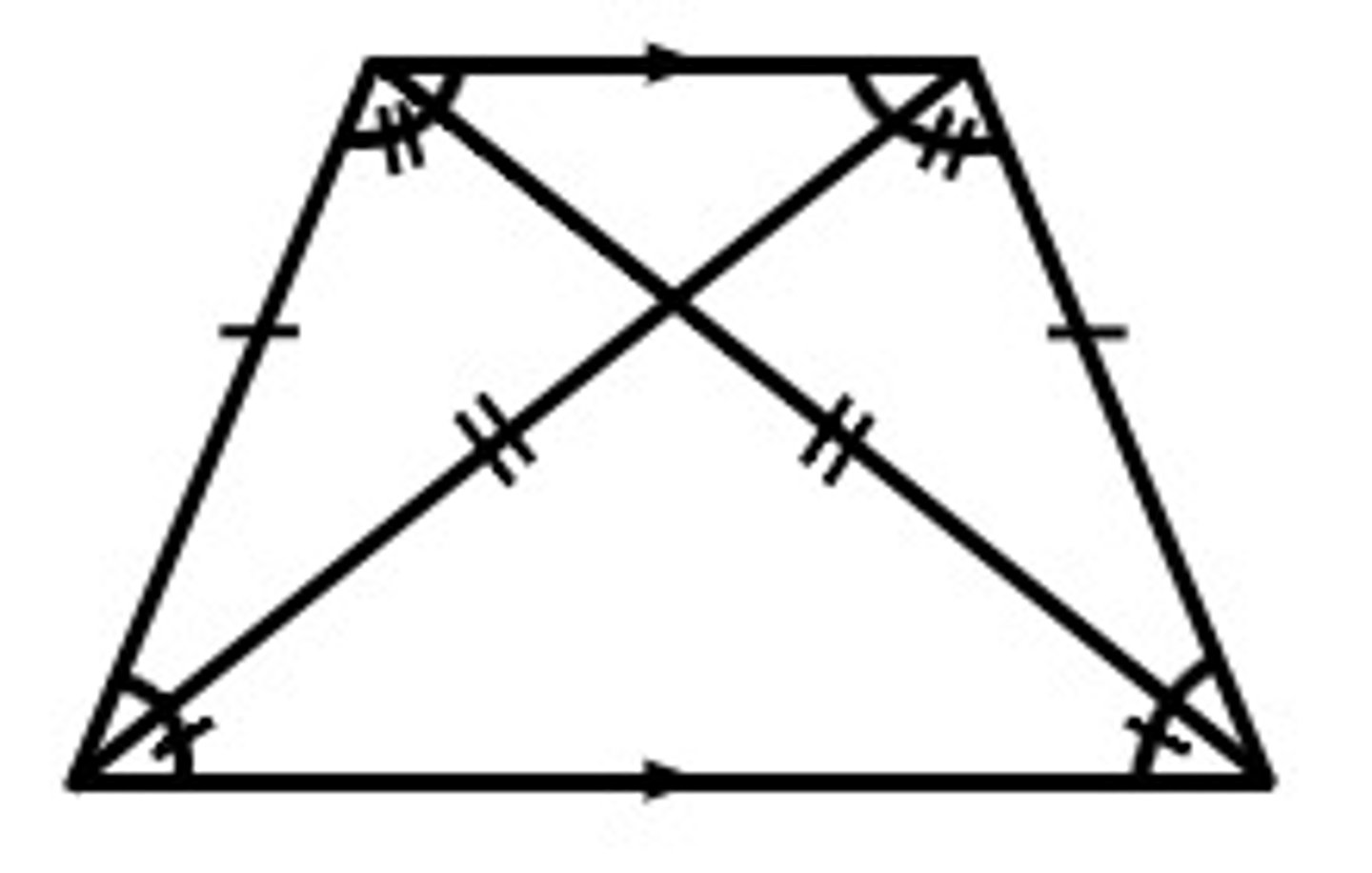
rectangle properties

parallelogram properties (opposite sides congruent). All right angles, diagonals are congruent

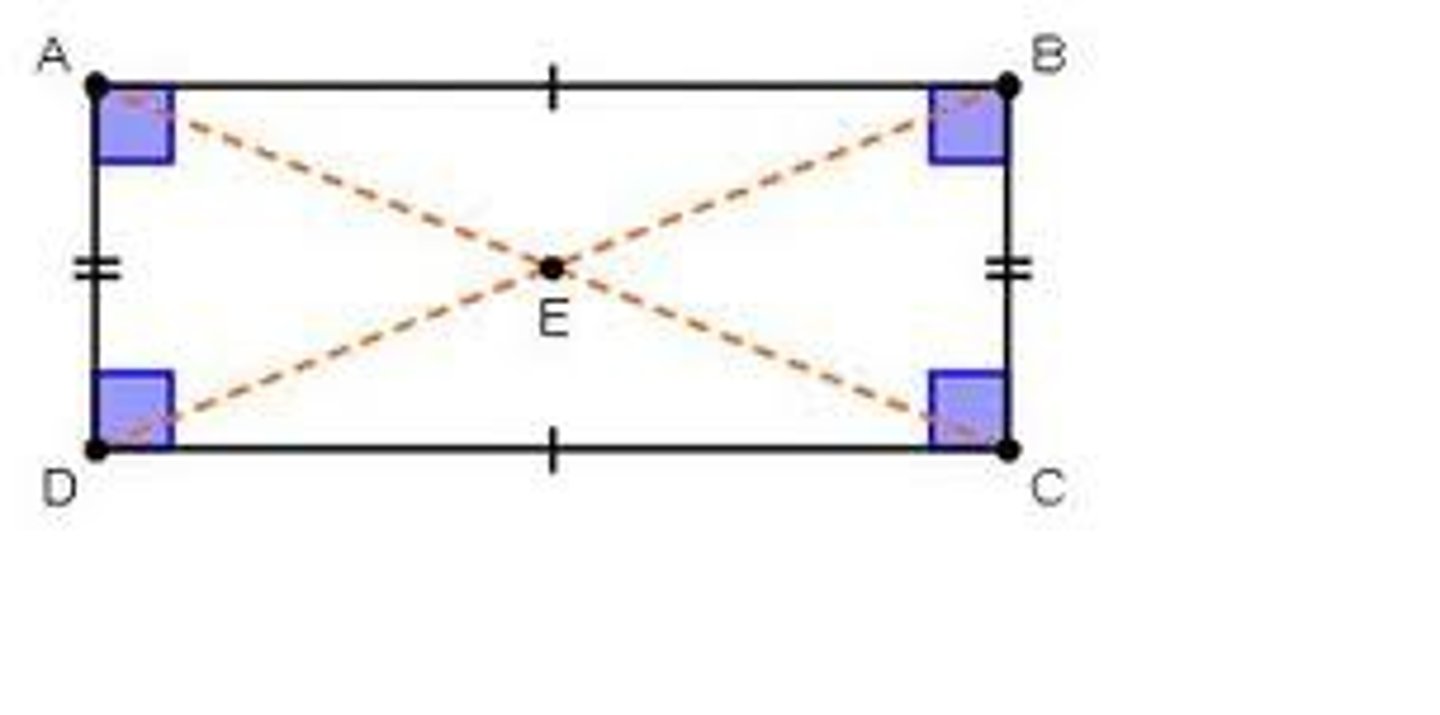
rhombus properties

parallel sides, opposite angles are congruent, consecutive angles are supplementary. all sides =. diagonals bisect angles.diagonals are perpindicular bisectors of each other DIAGNOLS FORM FOUR CONGRUENT ISOSCELES RIGHT TRIANGLES

square properties

(for proofs) any one of the parallelogram + square + rhombus properties

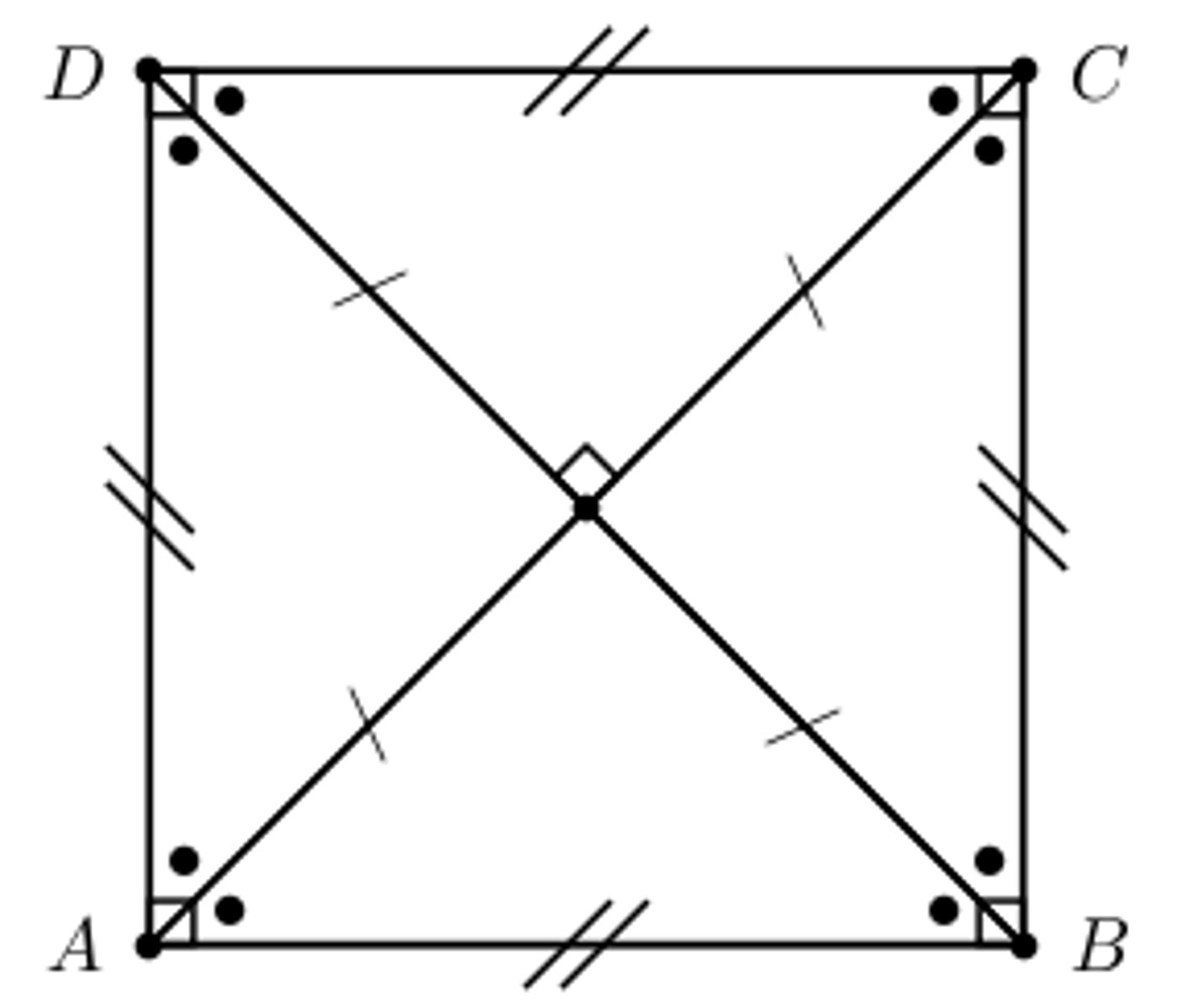
two lines are parallel

if the alternate interior angles formed are congruent

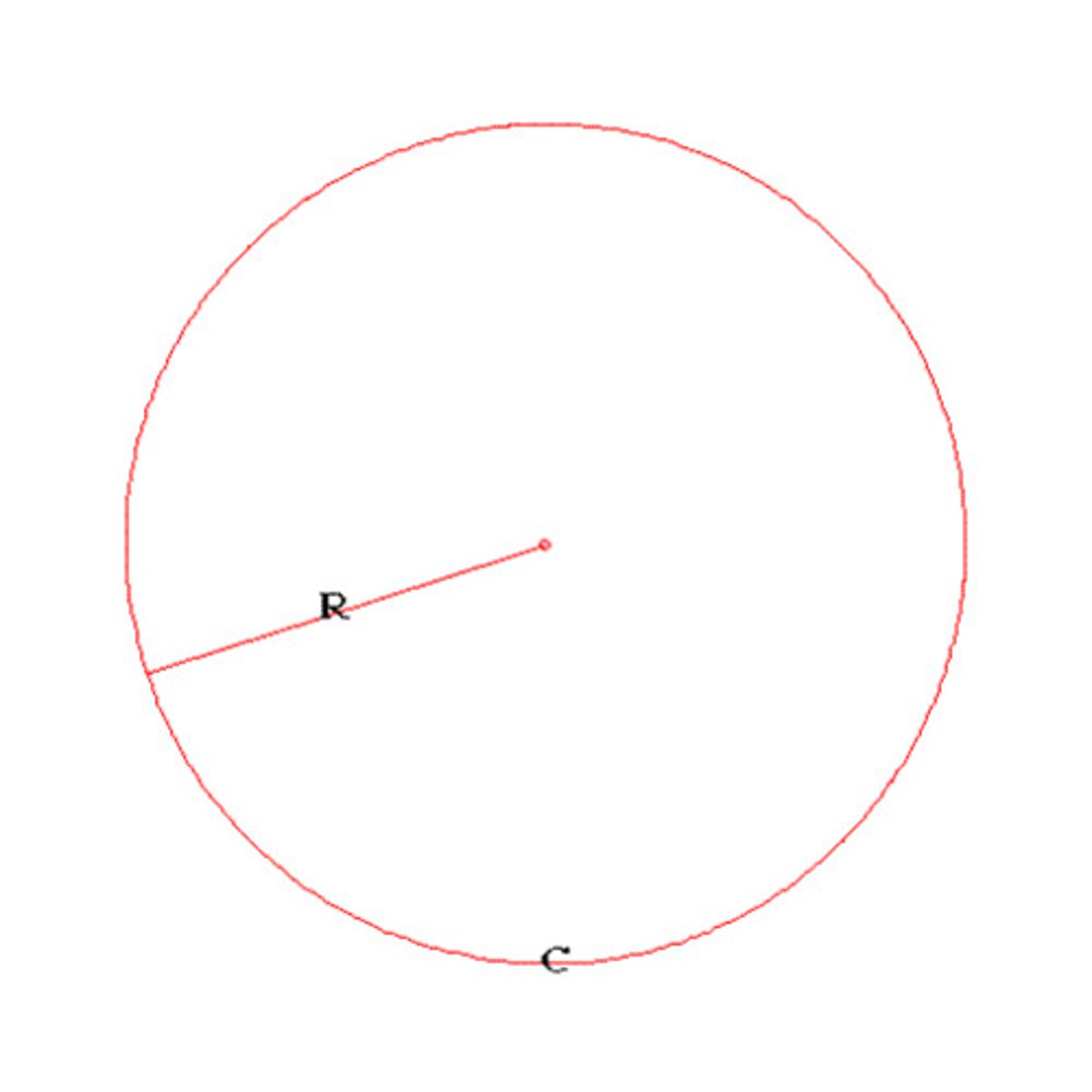
radius

a segment with one endpoint at the center of the circle and one endpoint on the circle

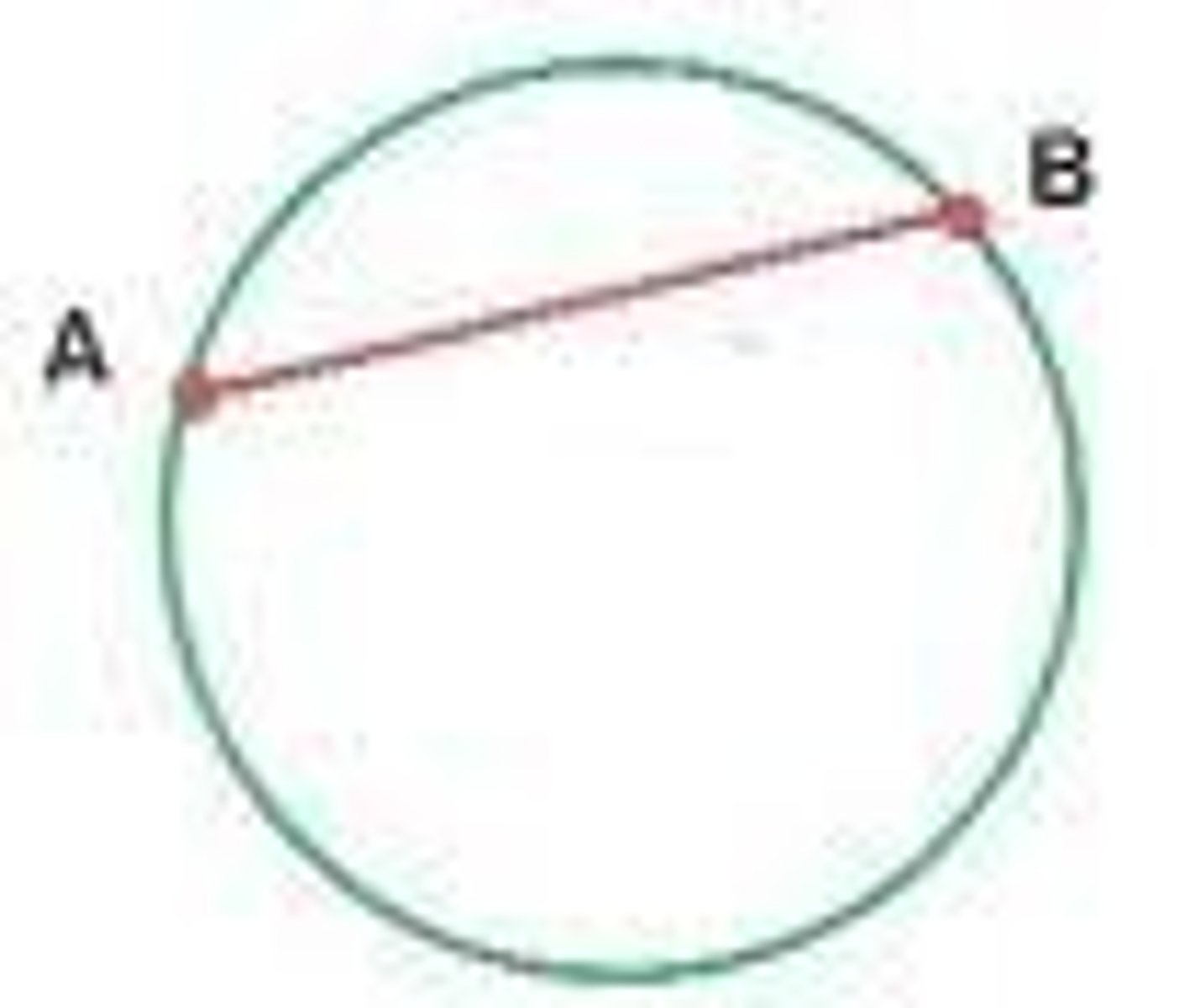
chord

a segment with both endpoints on the circle

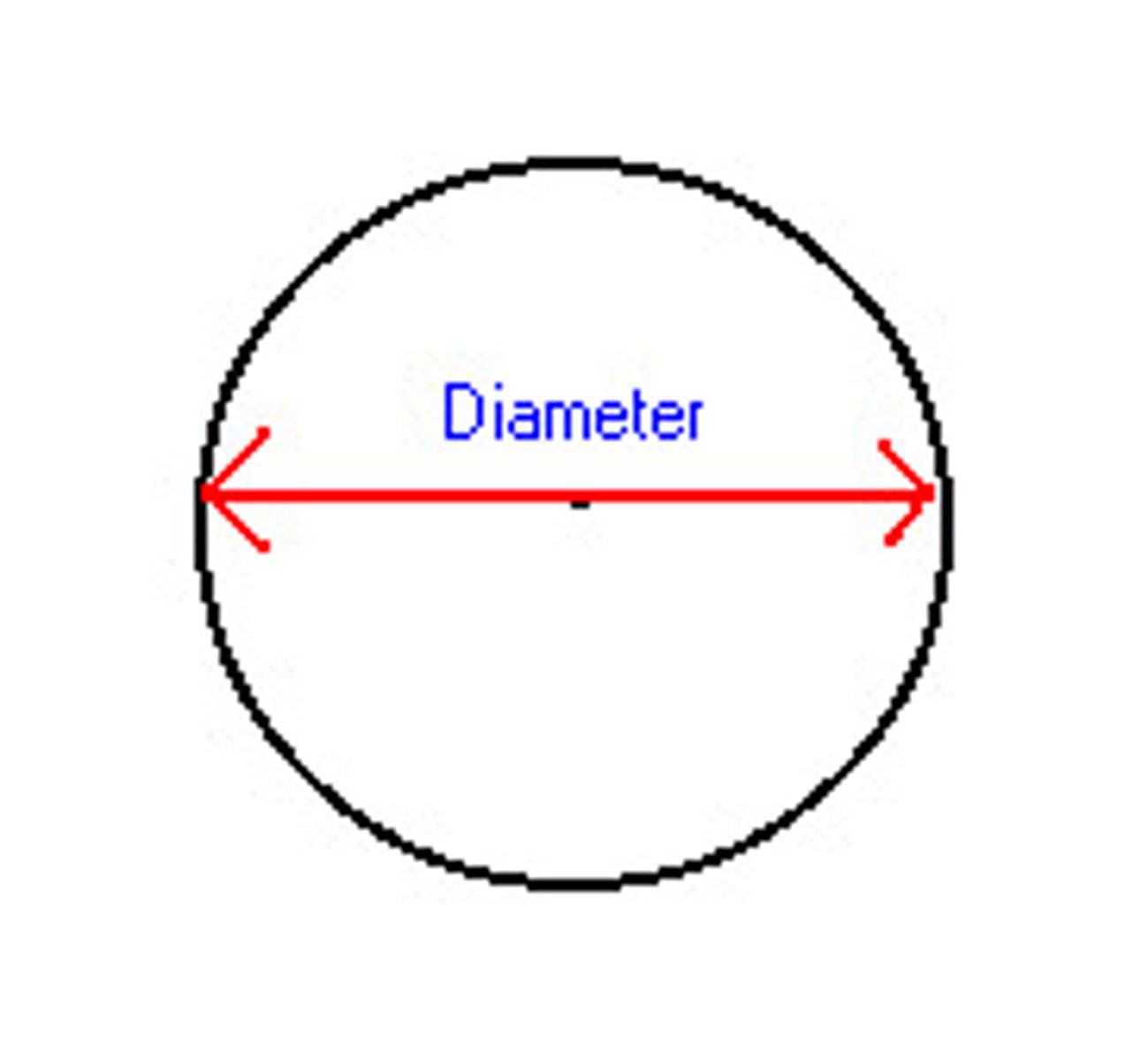
diameter

a chord that passes through the center of the circle

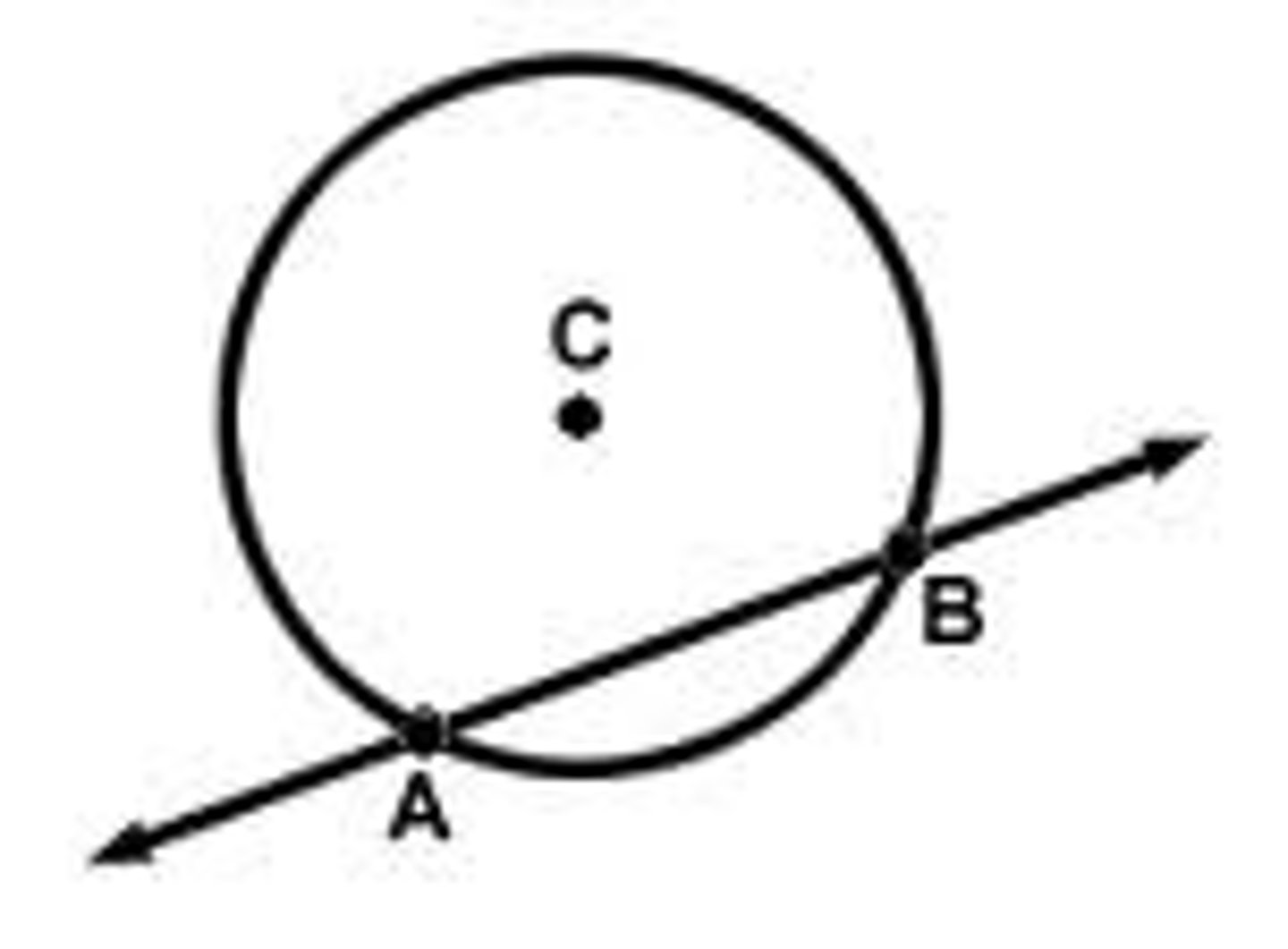
secant

a line that intersects a circle at exactly two points

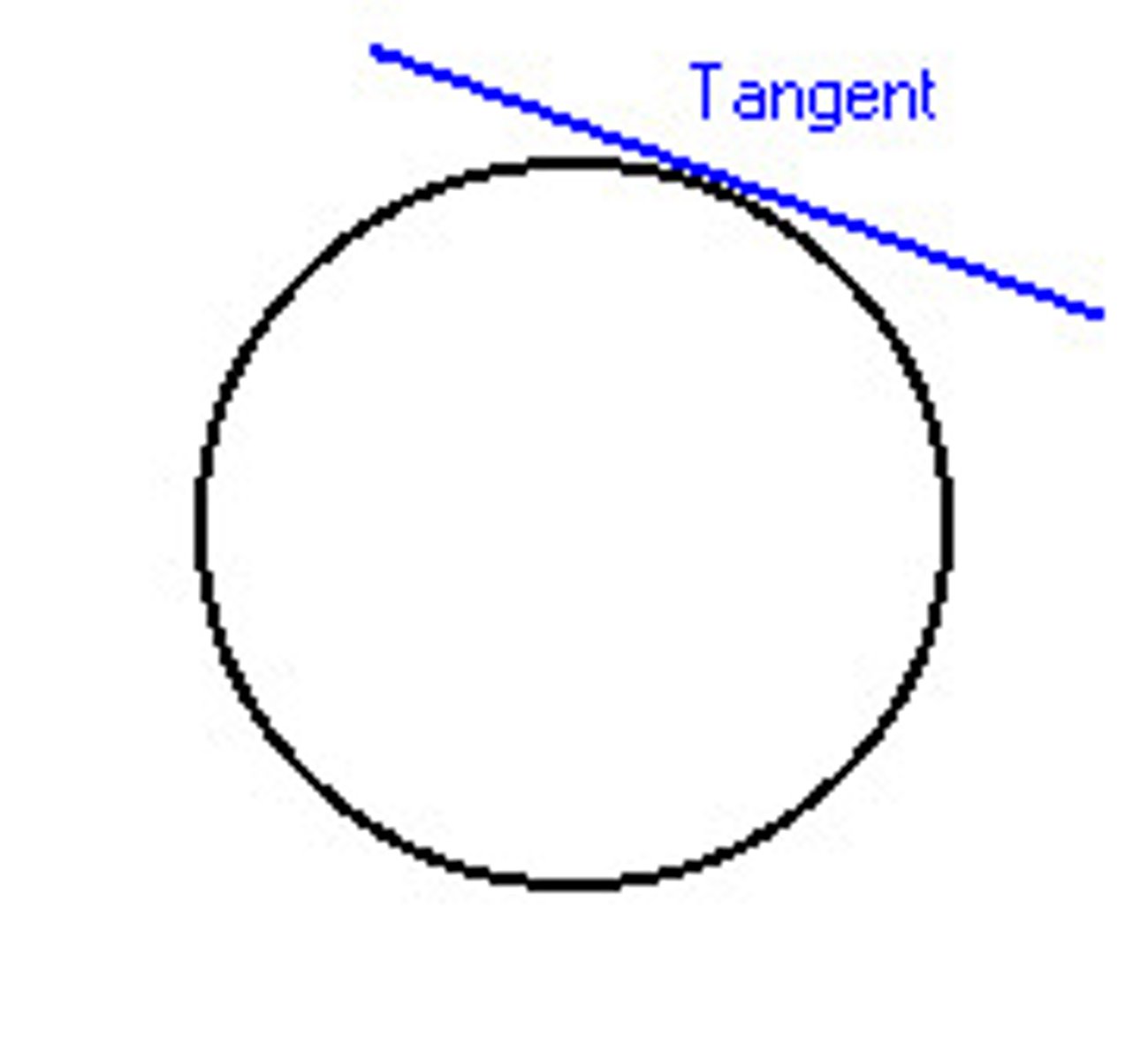
tangent

a line that intersects a circle at exactly at one point

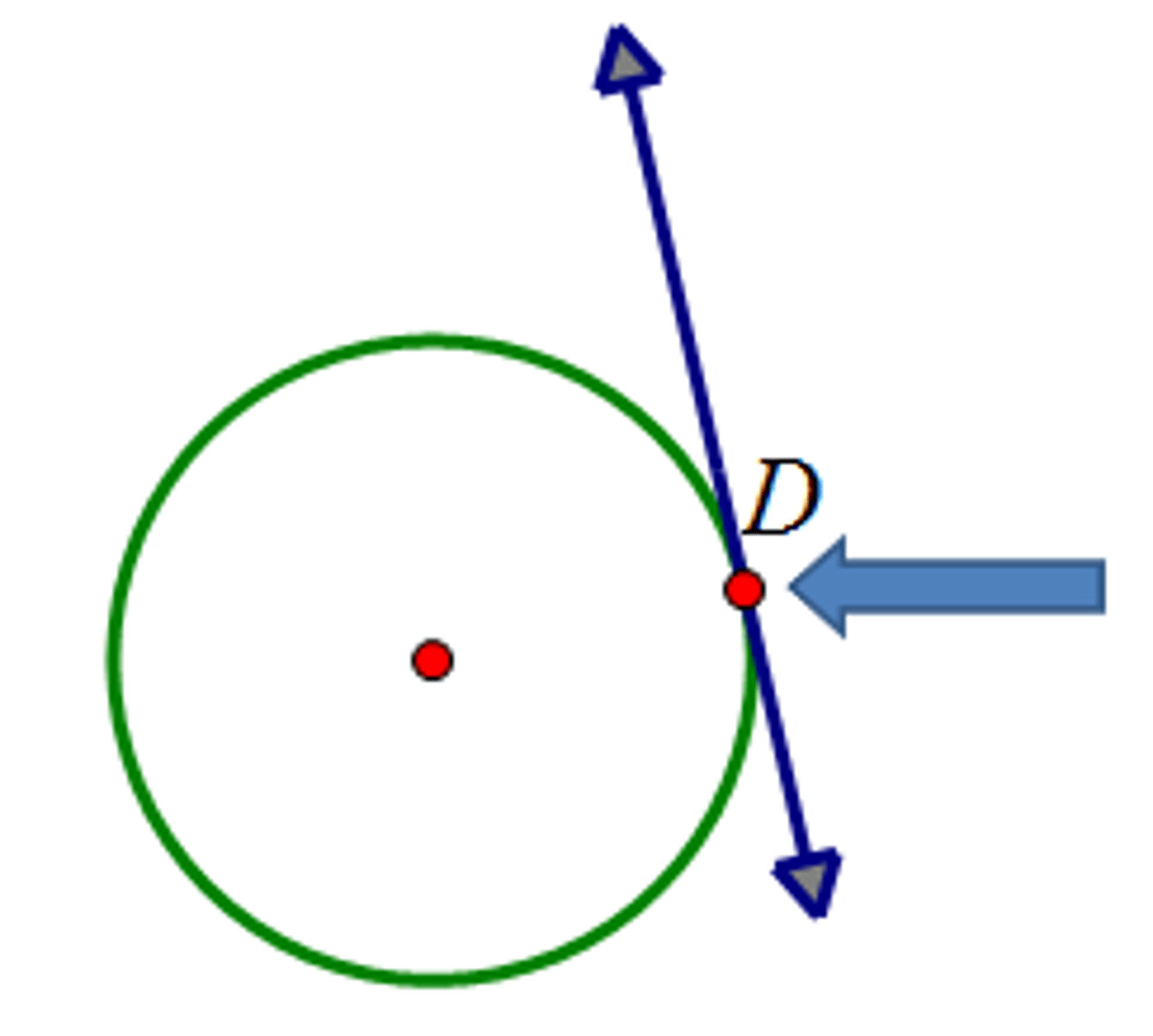
point of tangency

the point at which a tangent intersects a circle

radii properties

all radii of a given circle are congruent, two circles are congruent if and only if their radii are congruent

central angle theorem

the angle measure of an arc equals the measure of the central angle that interceps the arc

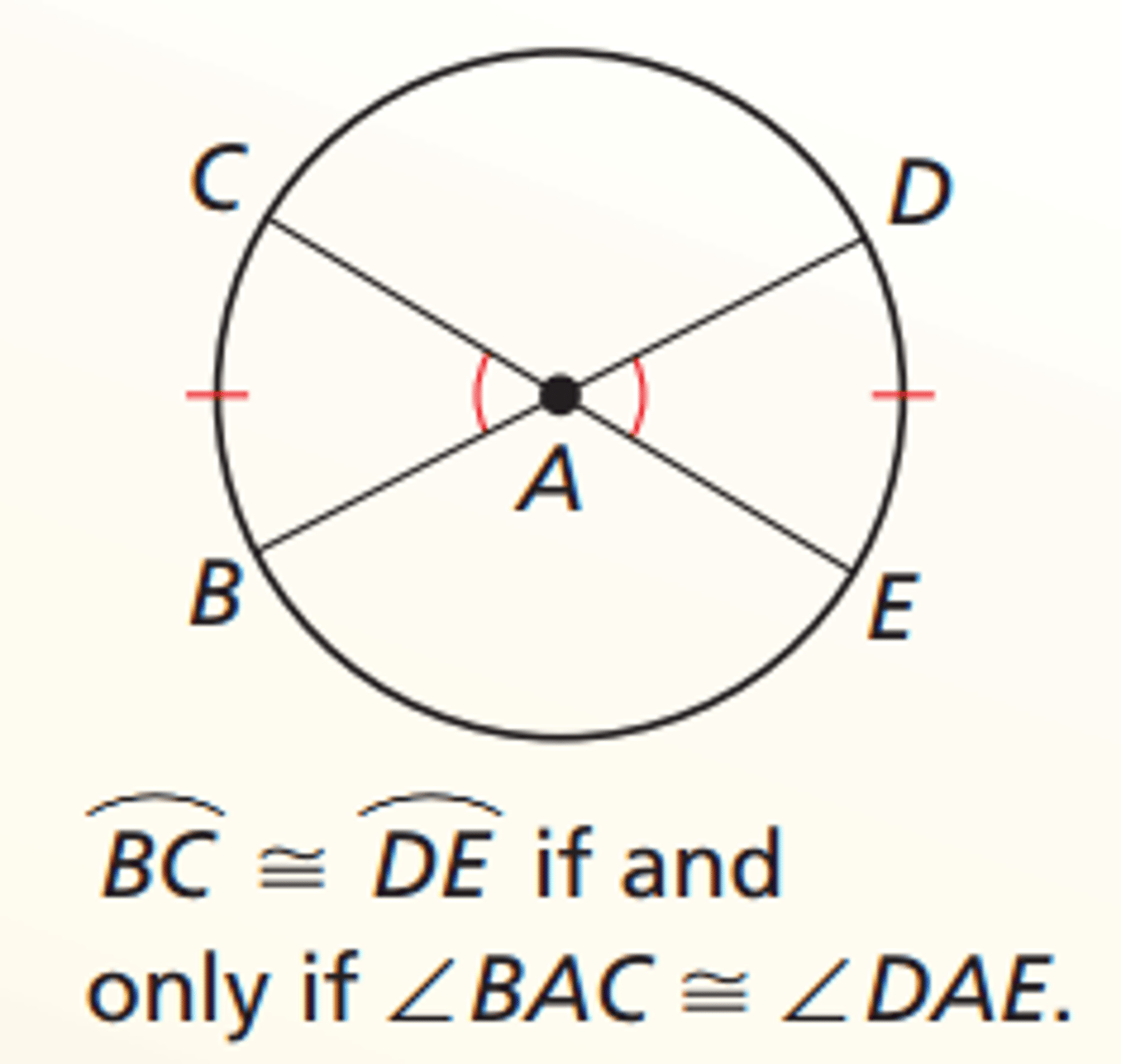
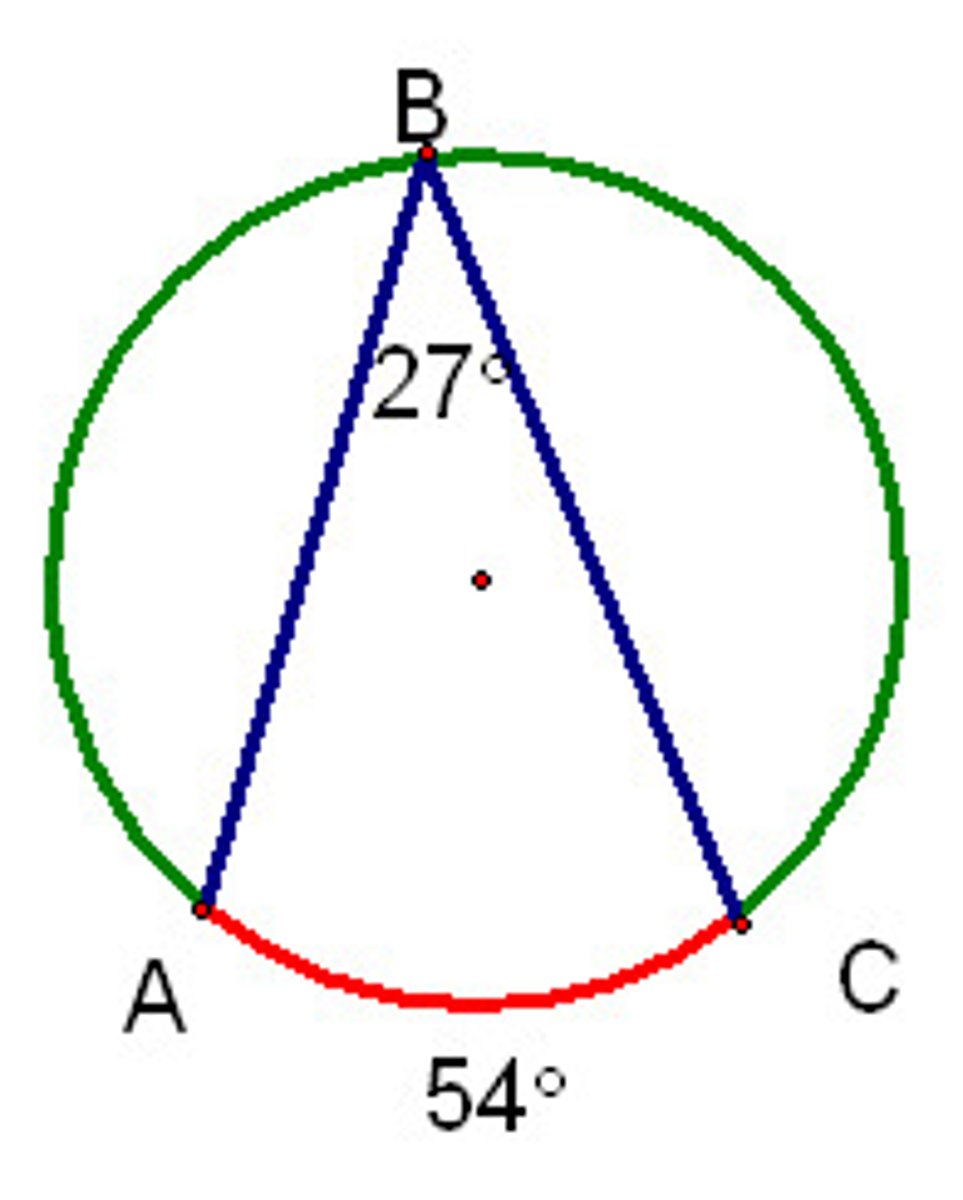
inscribed angle theorem

the angle measure of an arc equals twice the measure of the inscribedangle that interceps the arc

congruence chord theorem

congruent chords intercept congruent arcs on a circle. congruent arcs on a circle are intercepted by congruent chords

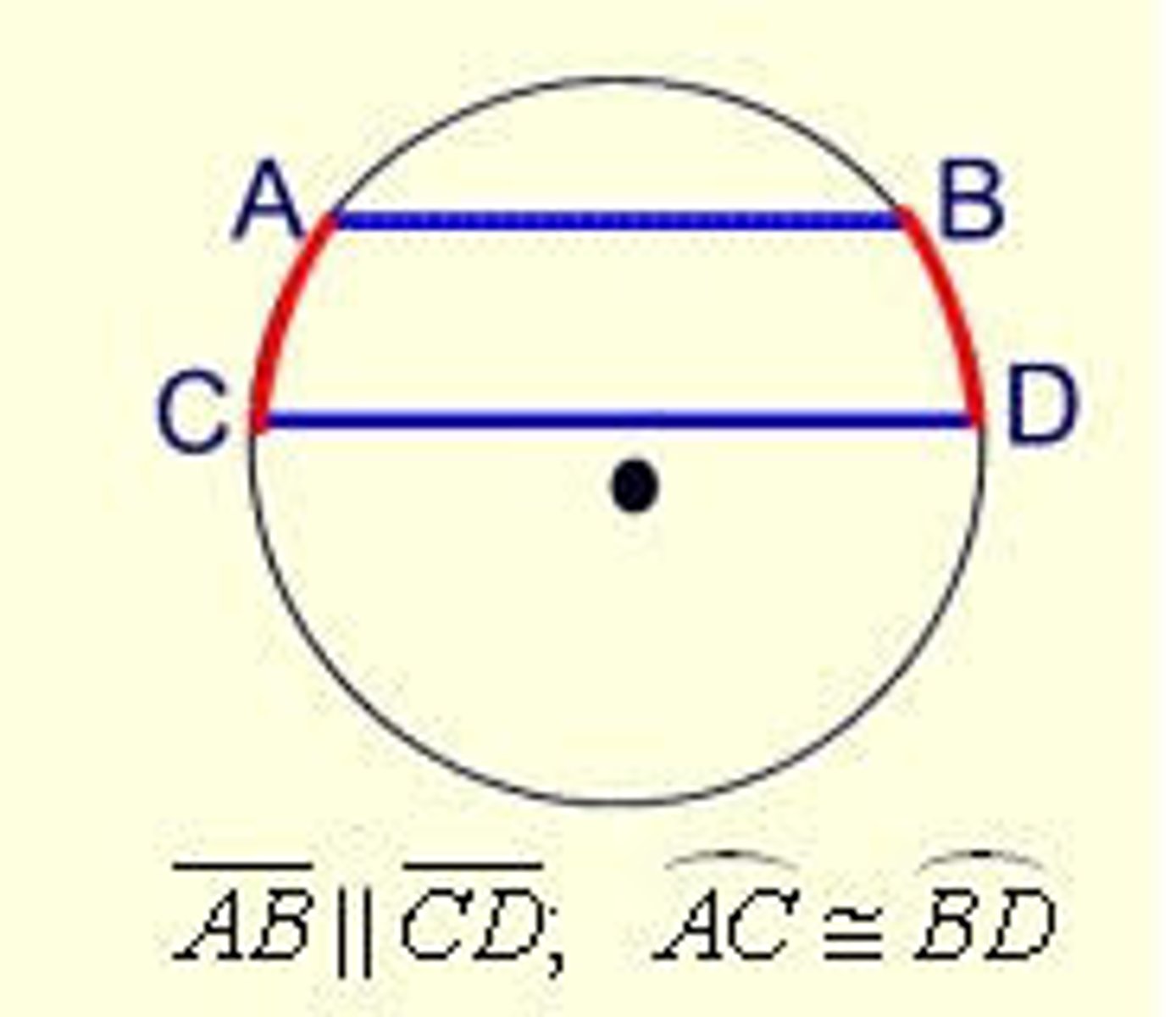
parallel chord theorem

the two arcs formed between a pair of parallel chords are congruent. if the two arcs formed between a pair of chords are congruent then the chords are parallel.

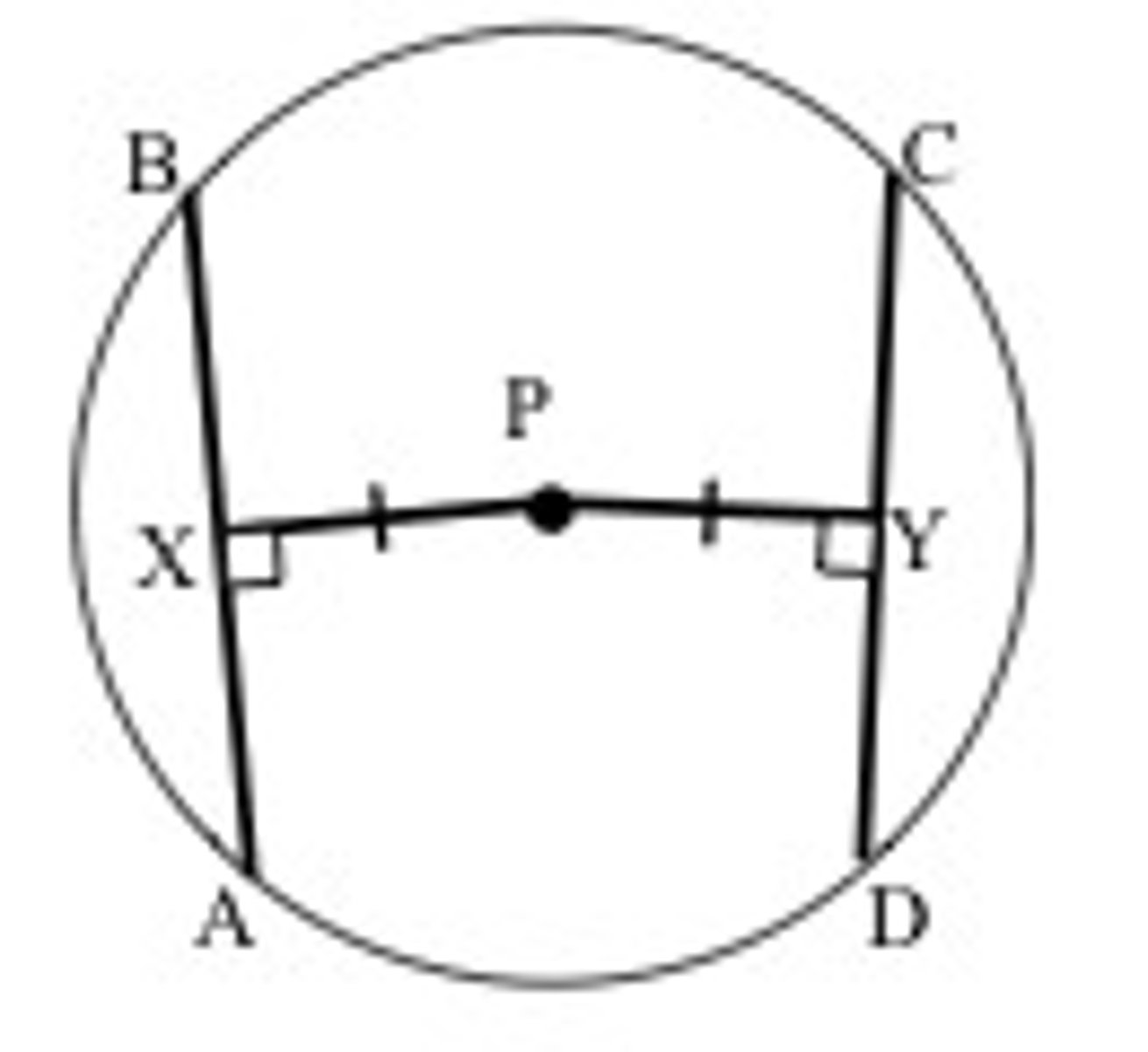
chord-perpindicular bisector theorem

the perpendicular bisector of any chord passes through the center of the circle. a diameter or radius that is perpindicular to a chord bisects the chord. A diameter or radius that bisects a chord is perpindicular to the chord

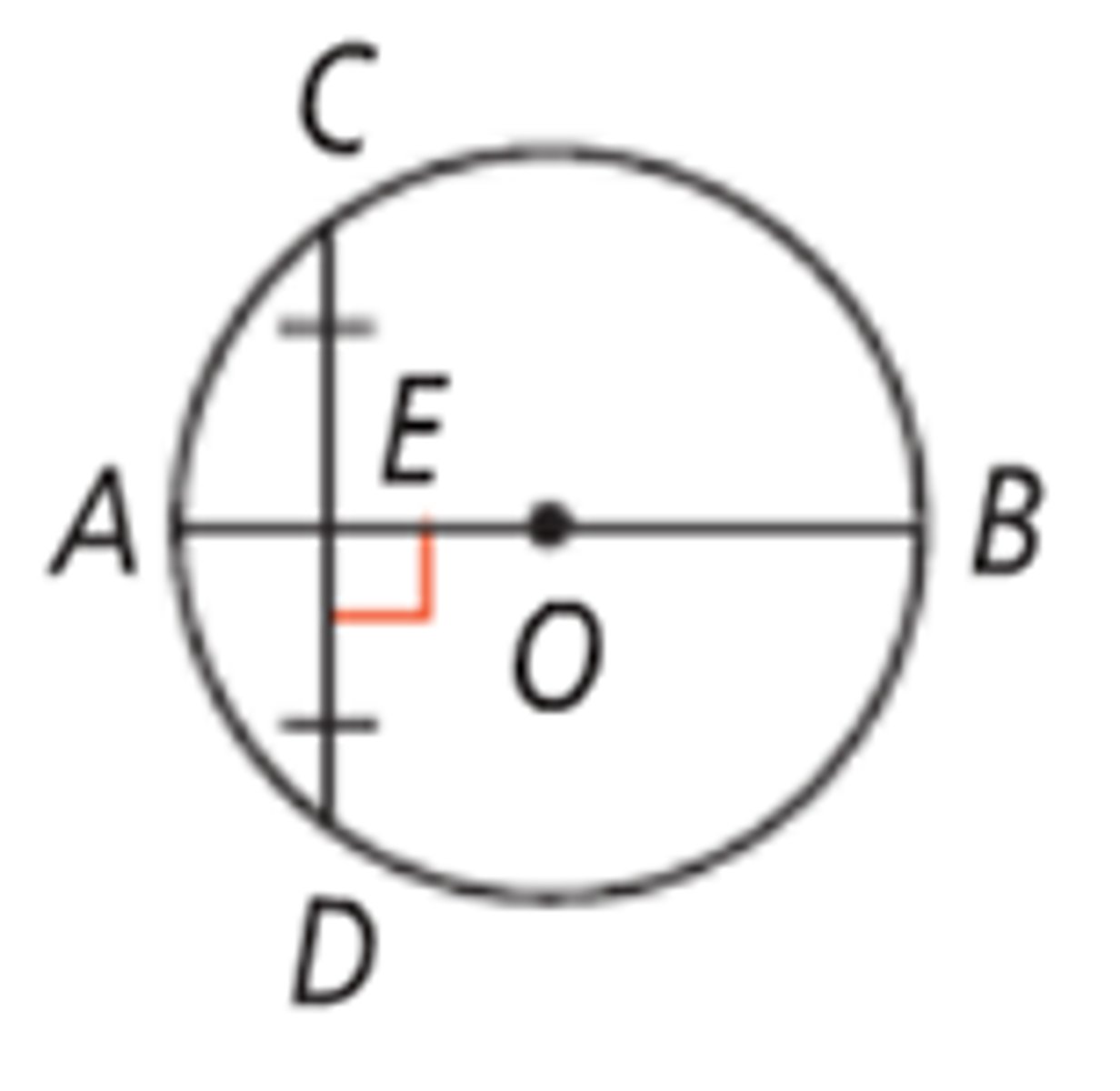
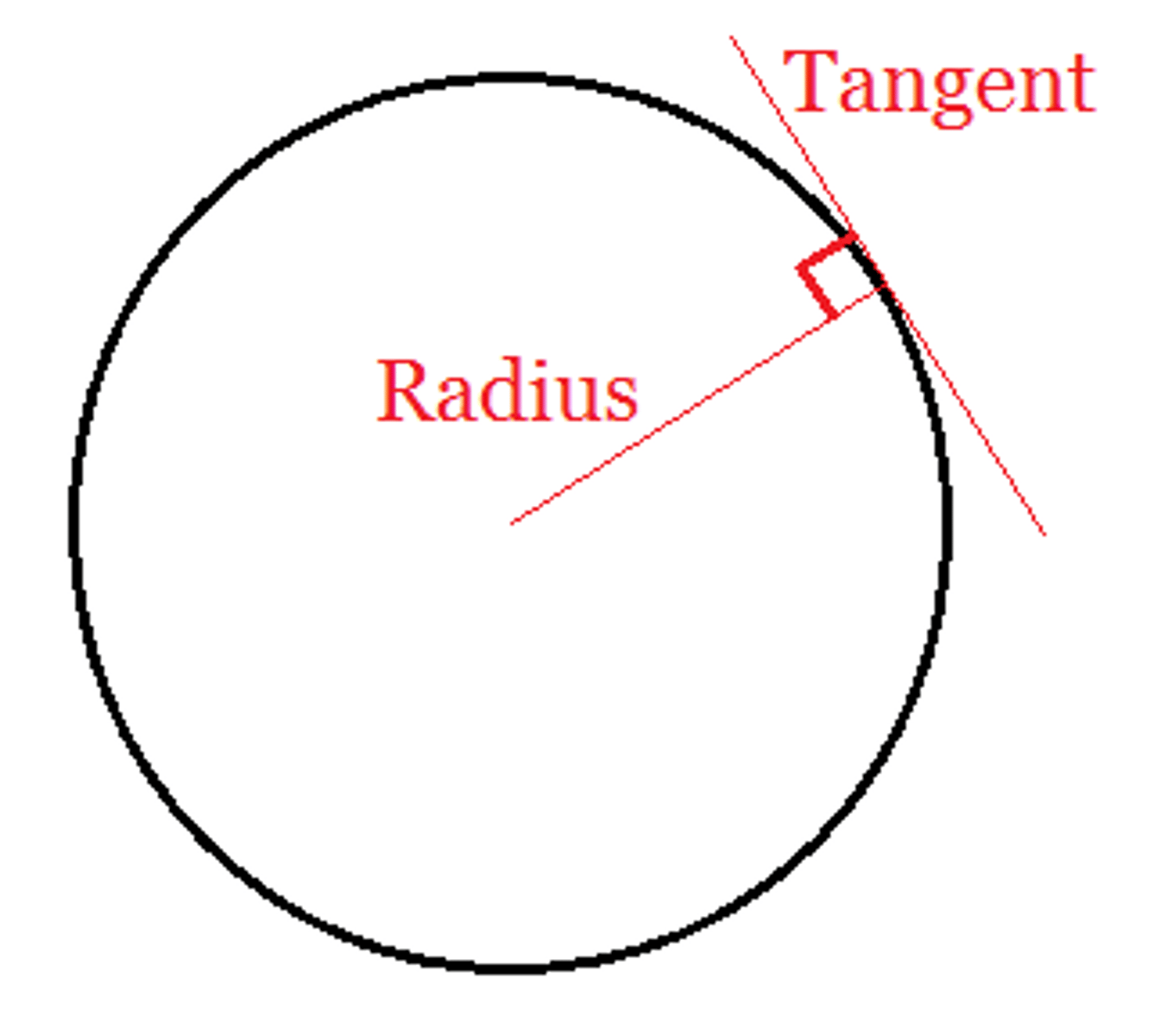
tangent radius theorem

a diameter or radius to a point of tangency is perpindicular to the tangent. A line perpindicular to a tangent at the point of tangency passes through the center of the circle

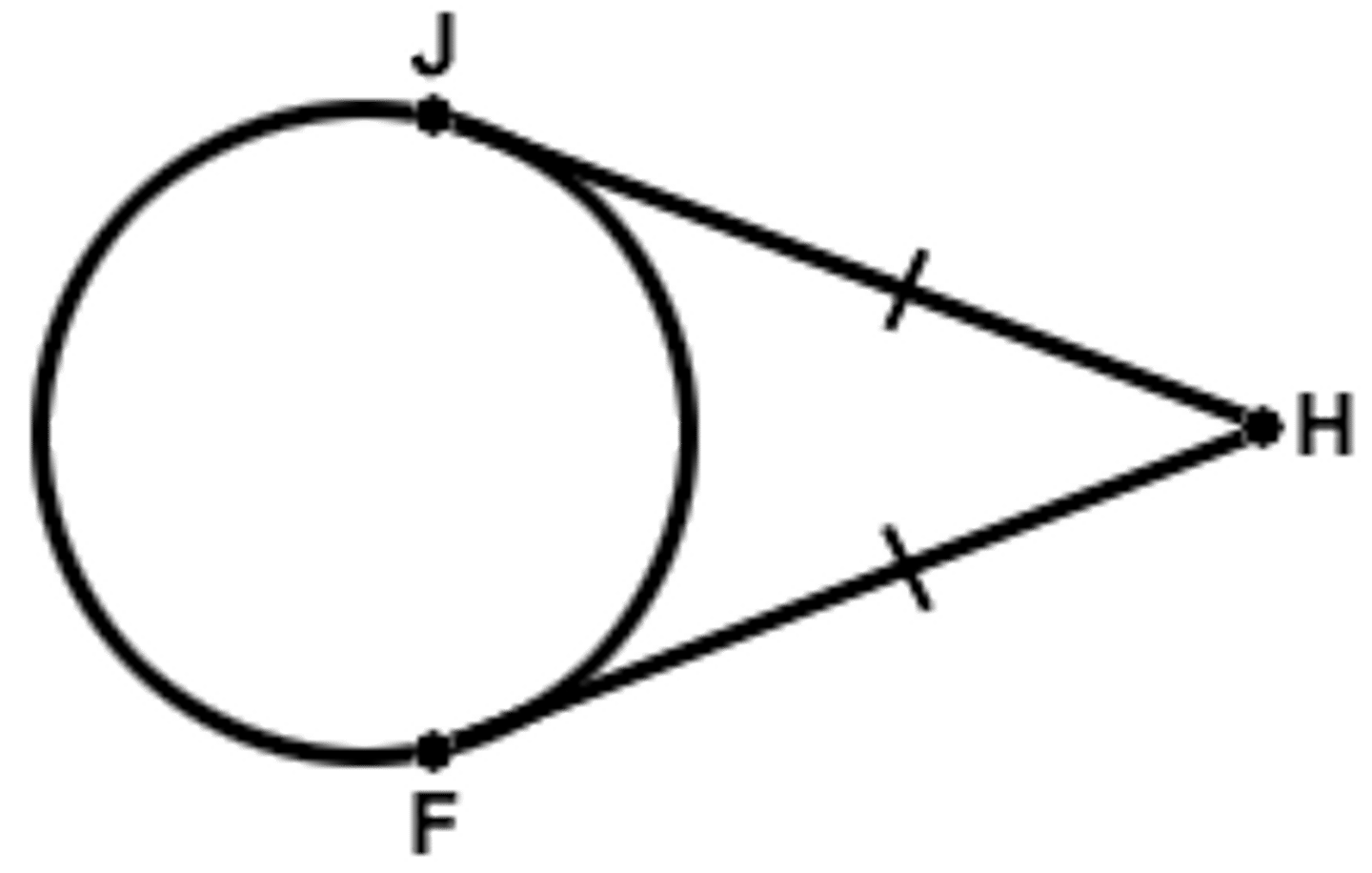
congruent tangent theorem

given a circle and external point Q, segments between the external point and the two points of tangency are congruent

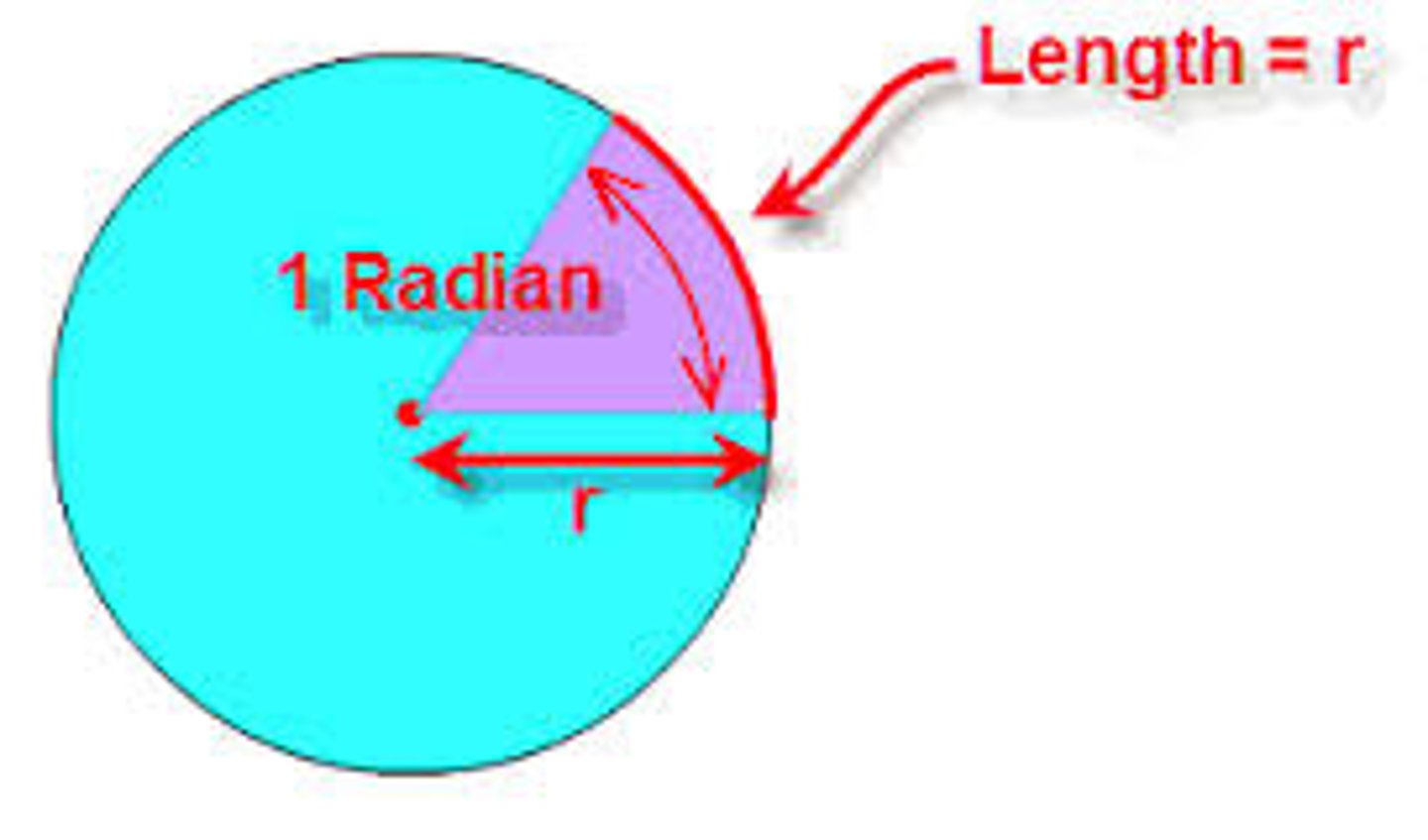
radian

π/180. A unit of angle measure. 2π is = to one complete revolution around a circle

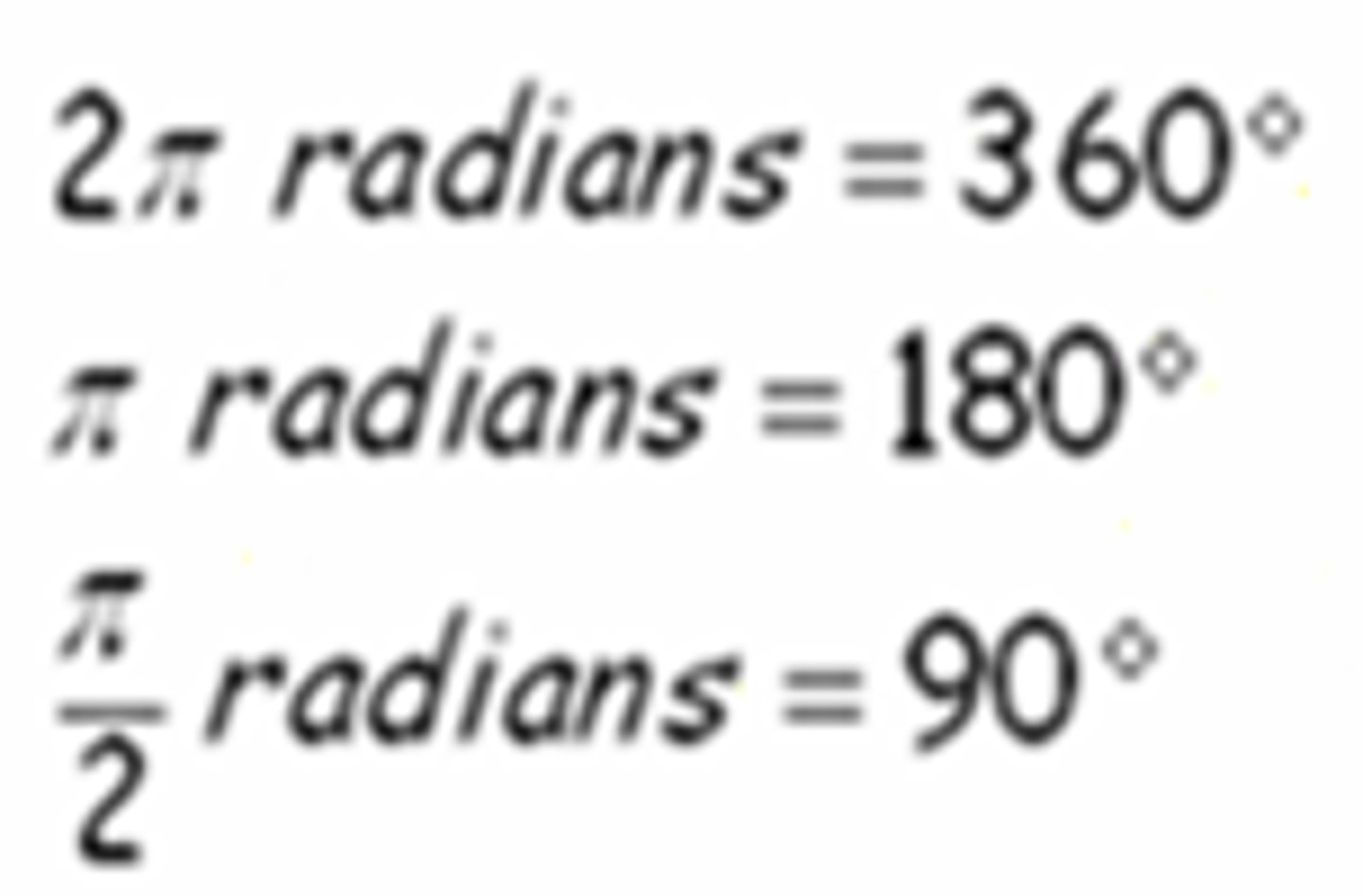
Radian area

1/2Rsquared(ø)

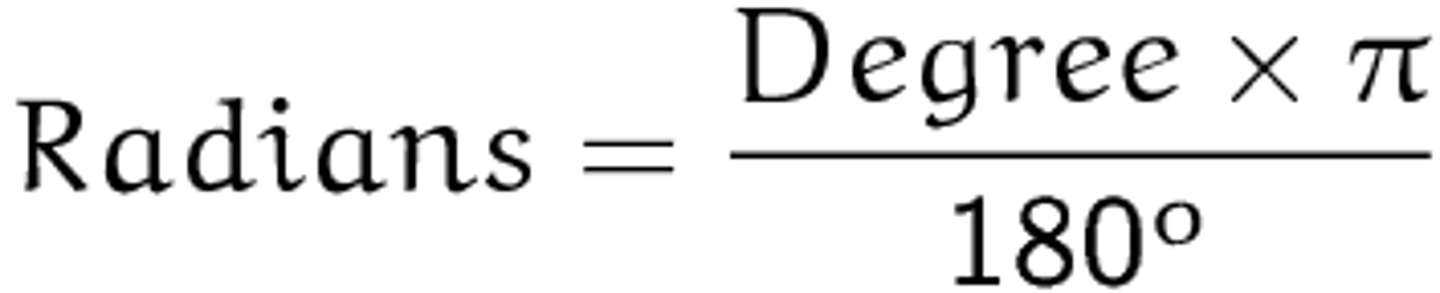
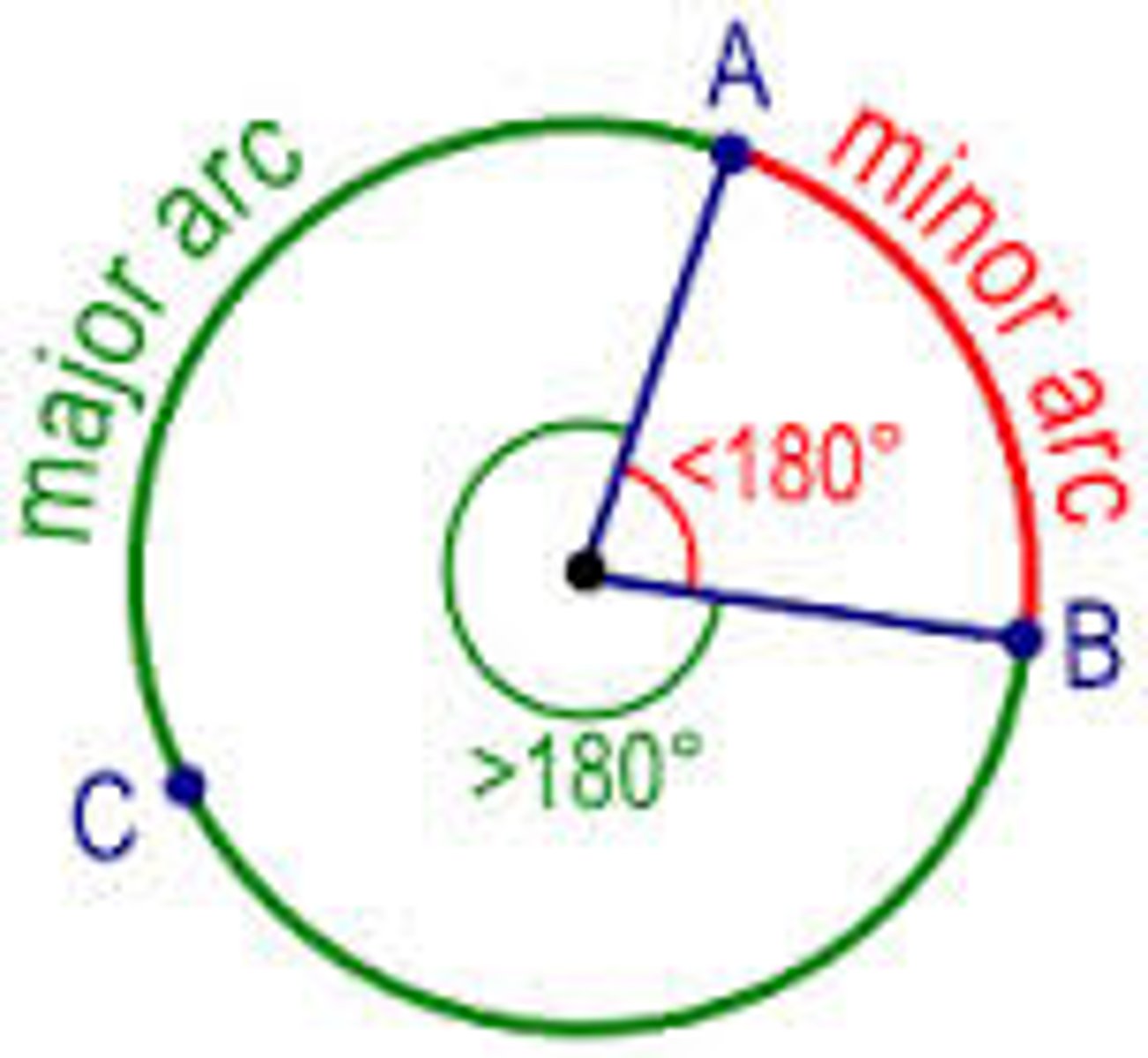
major arc

an arc with a measurement greater than 180º

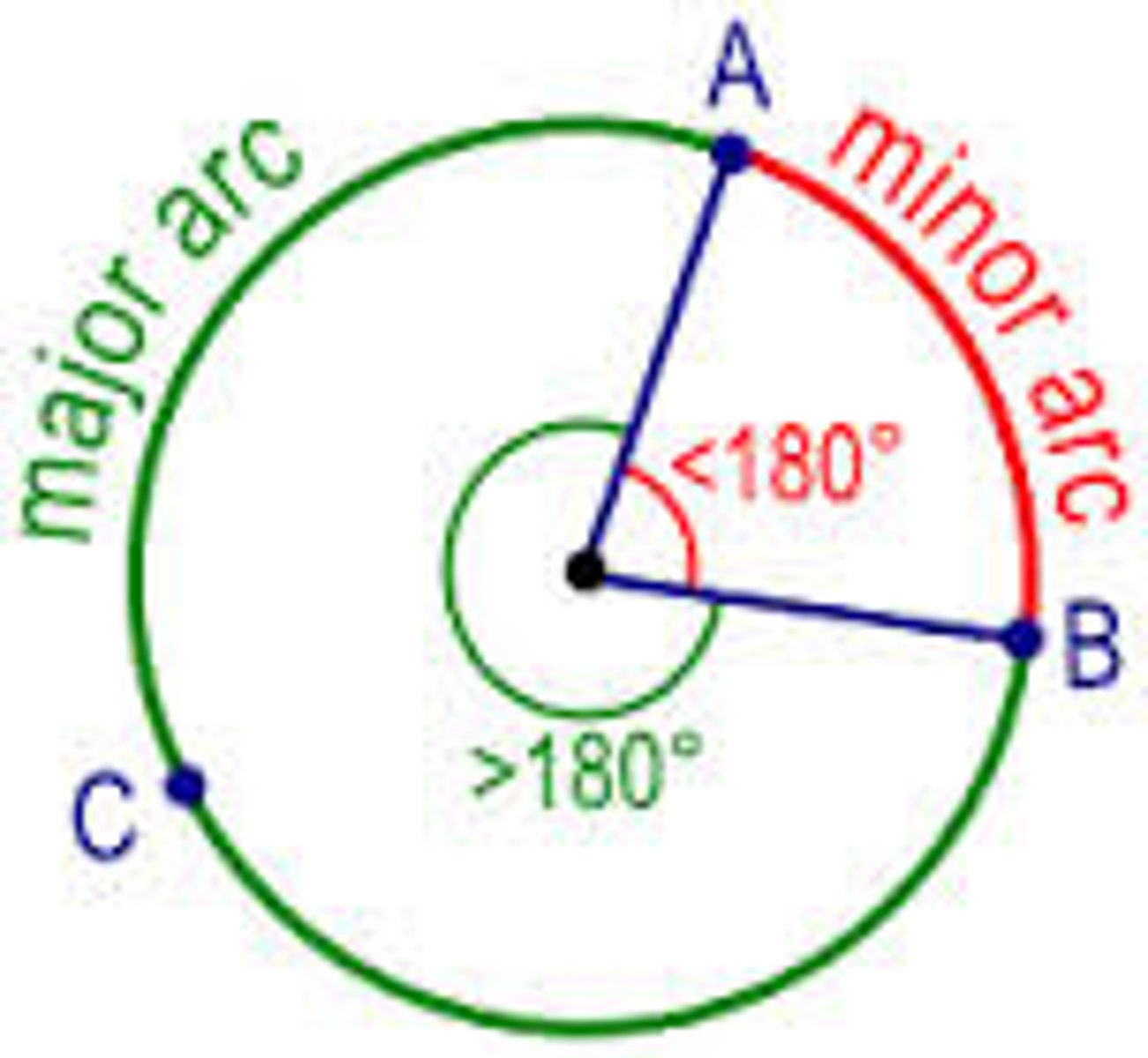
minor arc

an arc with a measurement less than 180º

semi-circular arc

an arc with a measurement of exactly 180º

angle of depression

the angle formed by the horizontal and the line of sight when looking downward to an object

angle of elevation

the angle formed by the horizontal and line of sight when looking upward an object

angle of rotation

the angle measure by which a figure or point spins around a center point

apex

the tip of a pyramid or cone or triangle

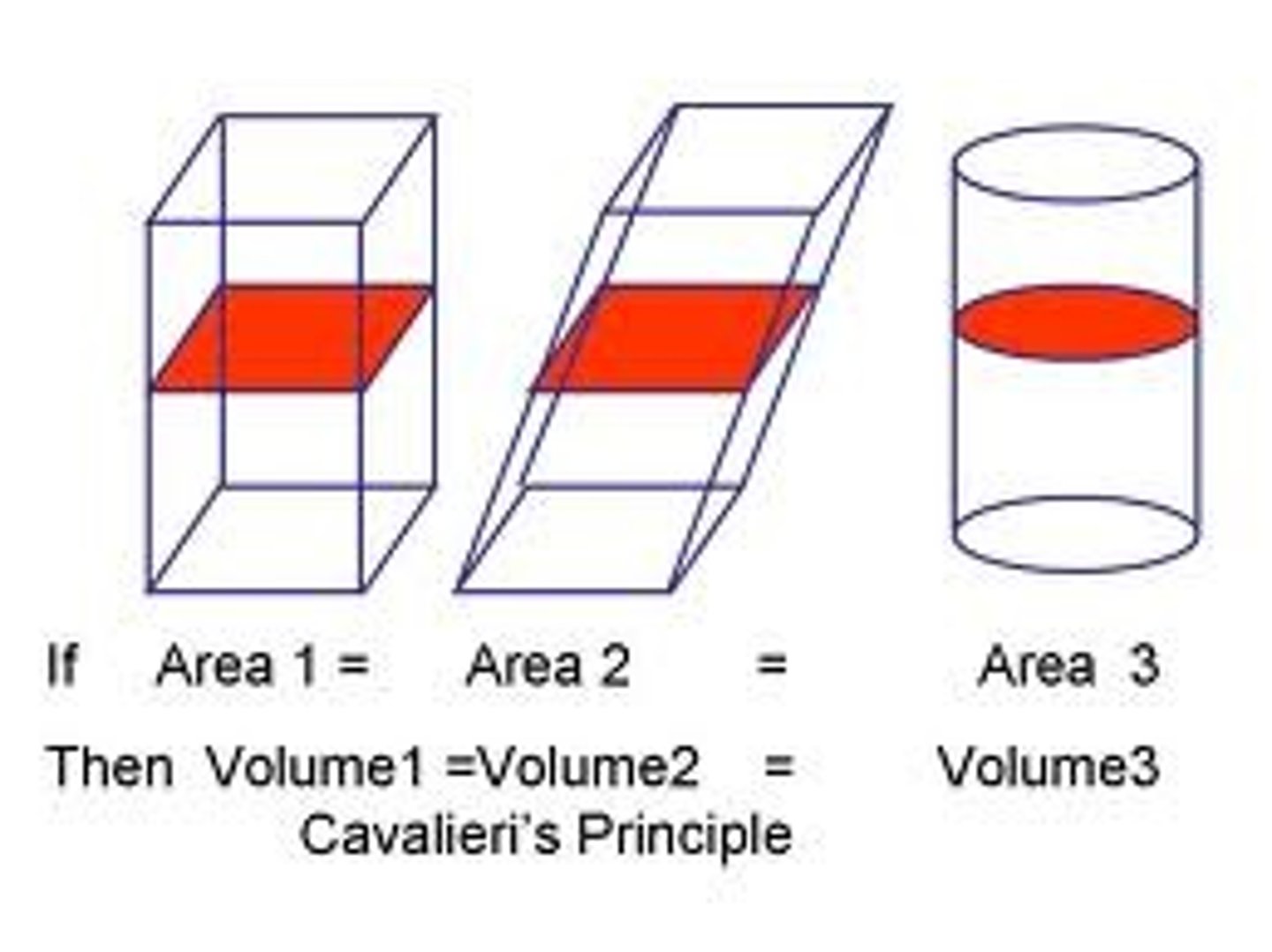
cavalieri's principle

if two solids are contained between two parallel planes, and every parallel plane between these two planes intercepts regions of equal area, then the solids have equal volume. Also, any two parallel planes intercept two solids of equal volume

center-radius equation of a circle

(x - h)squared + (y - k)squared = rsquared

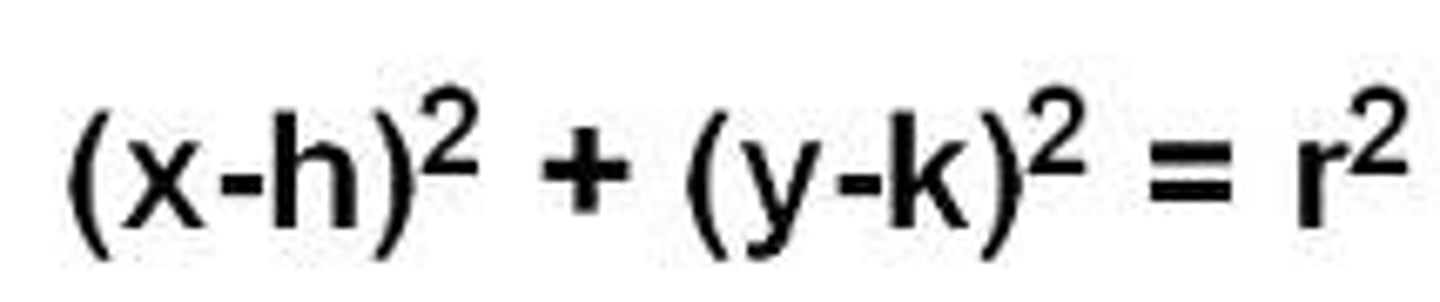
coincide (coincedent)

figure that lay entirely on one another

corresponding parts

a pair of parts (usually points, sides, or angles) of two figures that are paired together through a specified relationship, such as a congruence or similarity statement or a transformation function

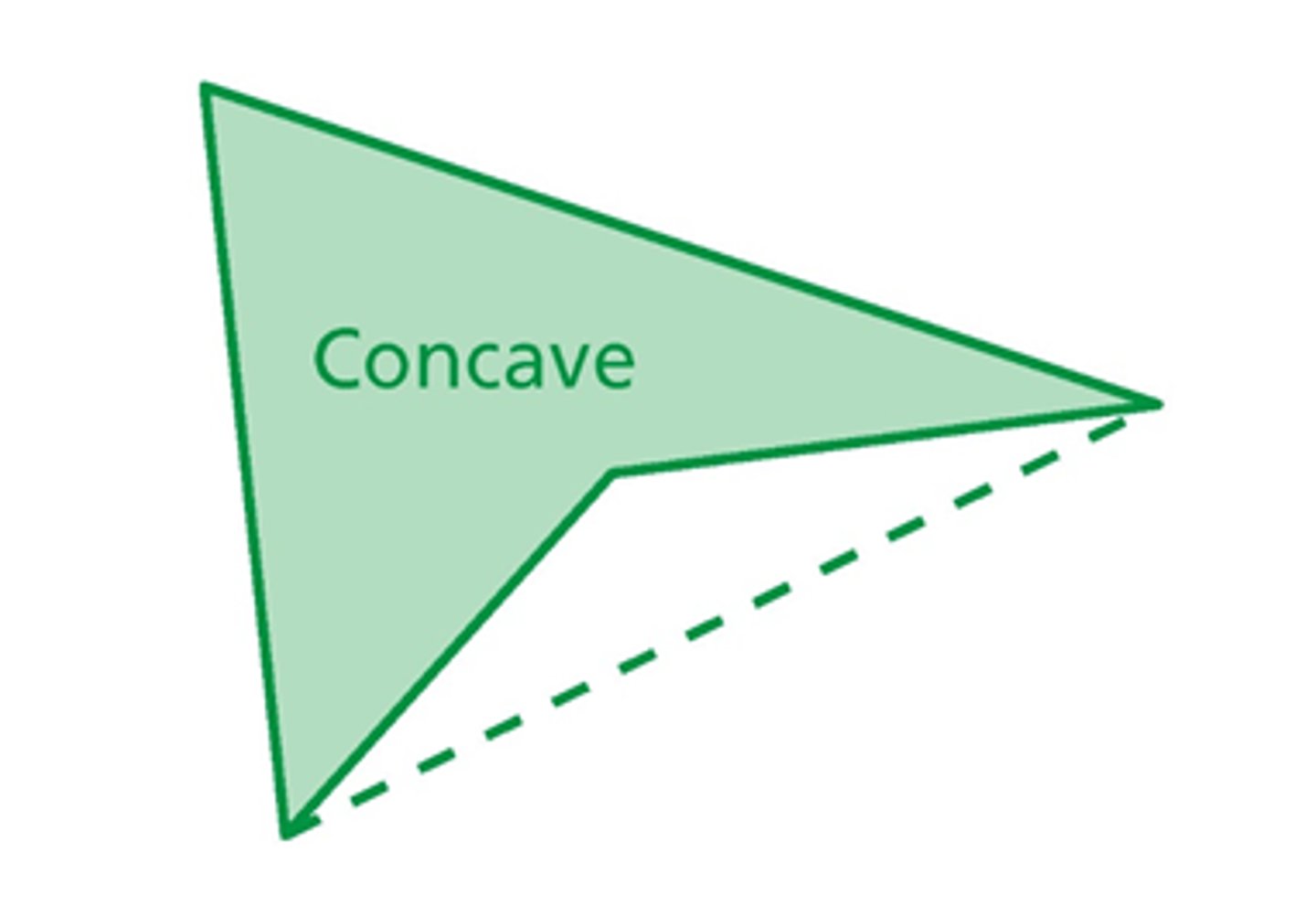
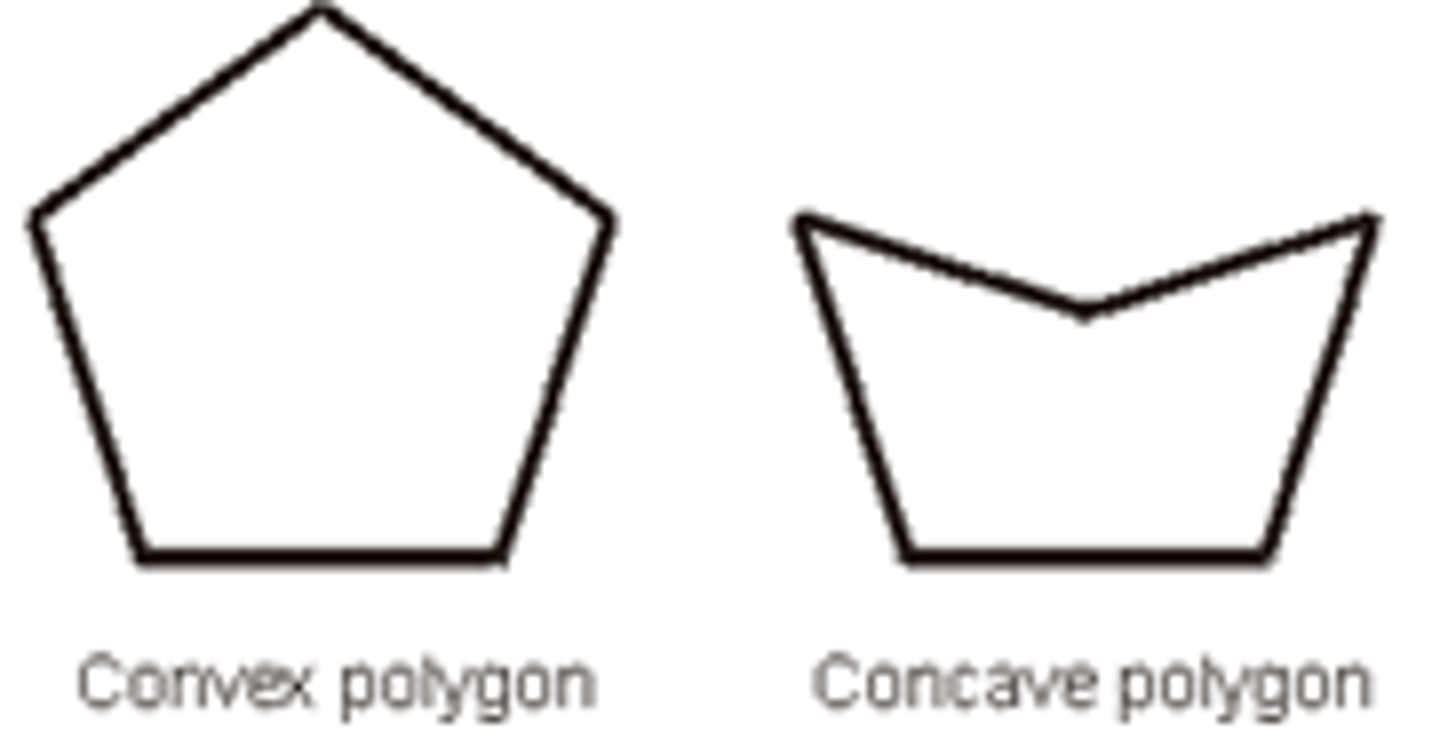
concave polygon

a polygon with at least one diagonal outside the polygon

concentric circles

circles with the same center

convex polygon

a polygon whose diagonals all lie within the polygon

CPCTC

corresponding parts of congruent triangles are congruent

direct transformation

a transformation that preserves oriontation

equiangular

a figure whose angles all have the same measure

equidistant

the same distance from two or more points

equilateral

a figure whose sides all have the same length

glide reflection

the composition of a line reflection and a translation along a vector parallel (basically a translation and a reflection in a direction)

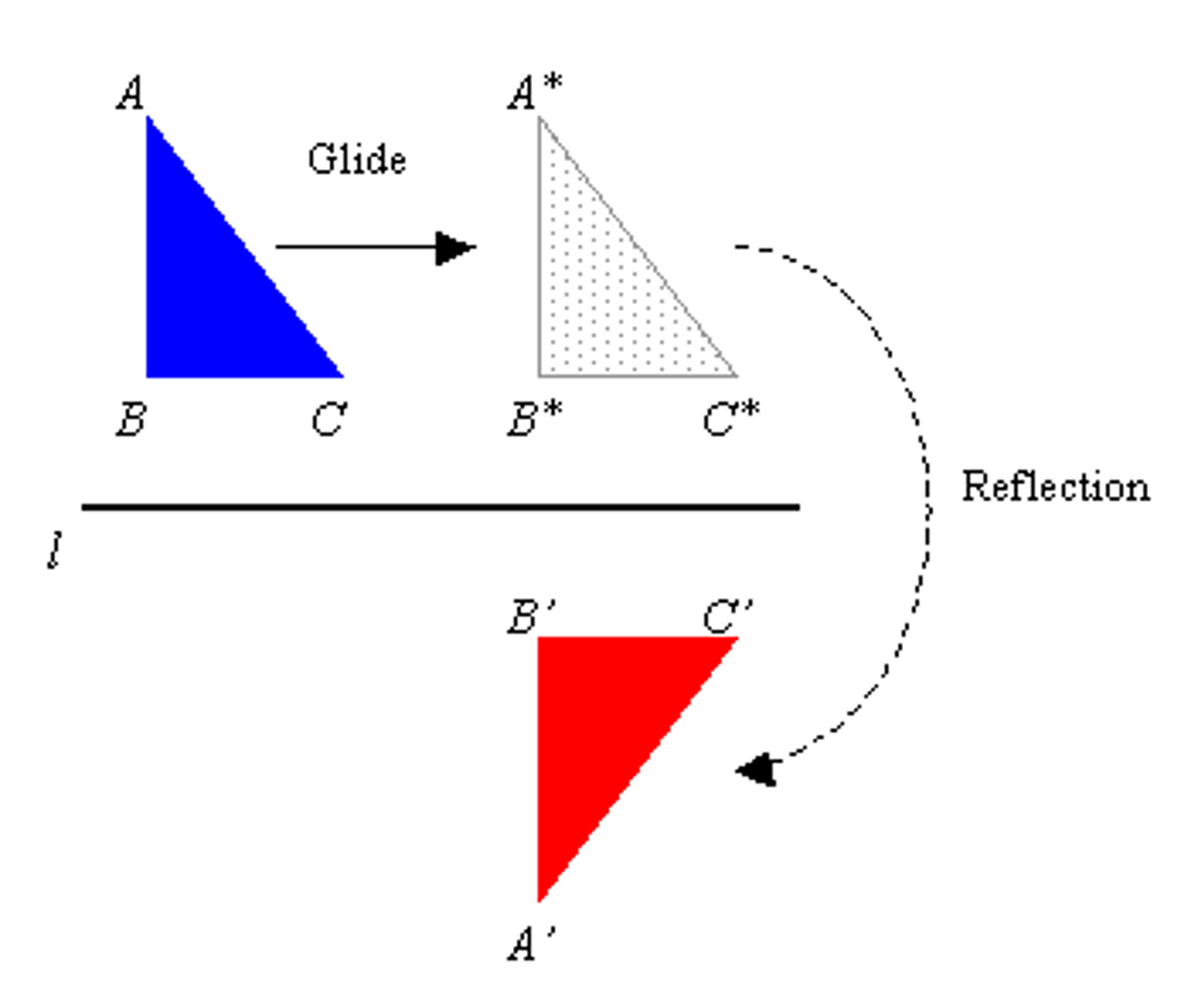
identity transformation

a transformation in which the pre-image and image coincide

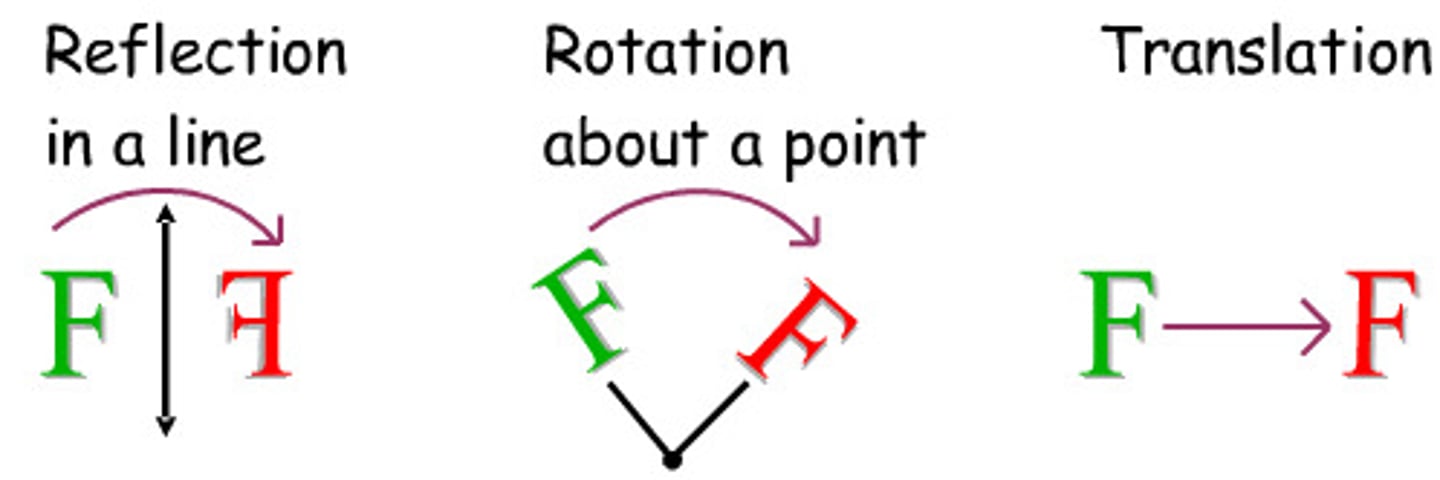
isometry/rigid motion

a transformation that preserves distance. the image and pre-image are congruent under a rigid motion. translations, reflections, and rotations are isometries

mean proportional (geometric mean)

the square root of the product of two numbers, a and b. If a/m=m/b, then m is the geometric mean

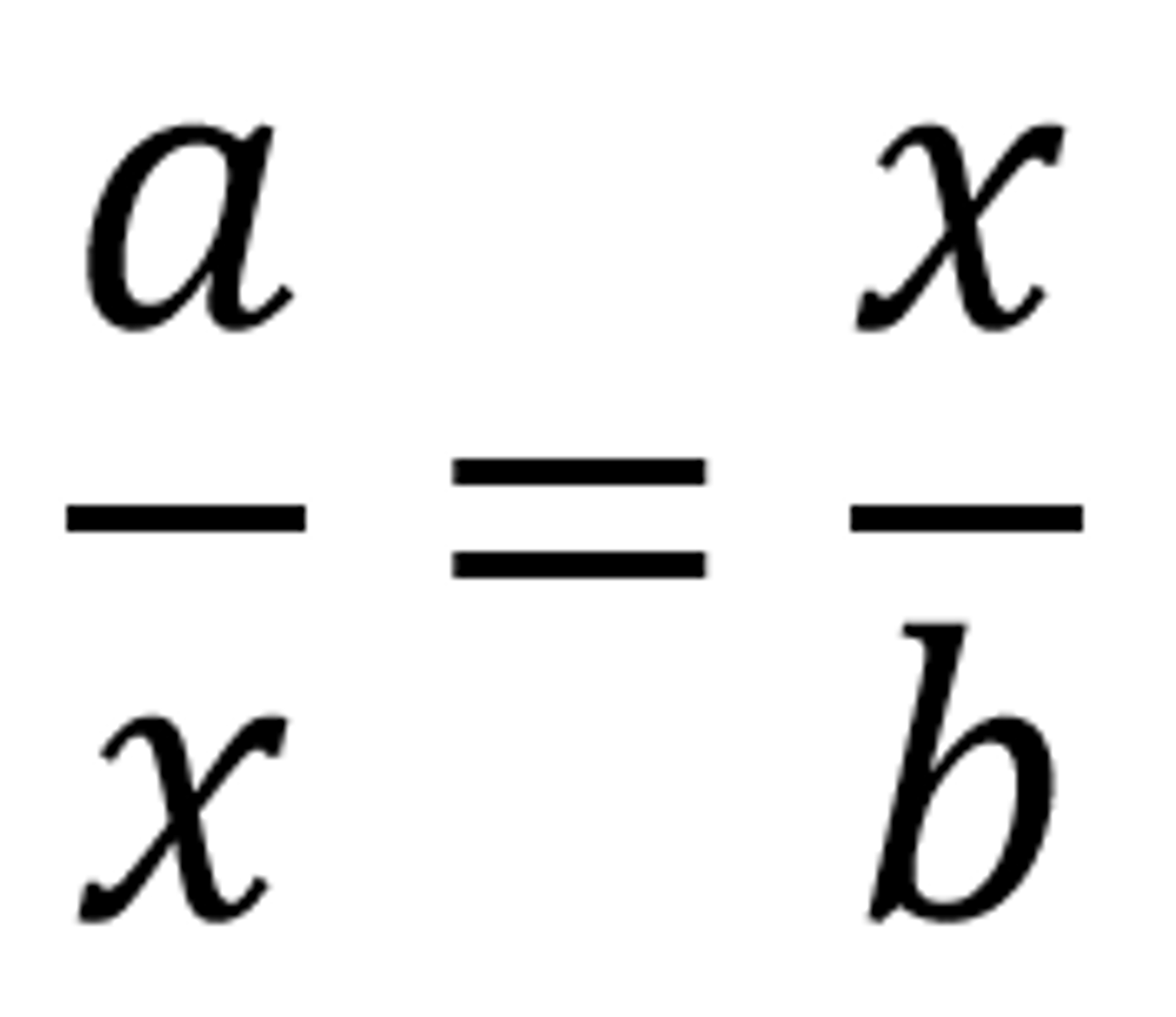
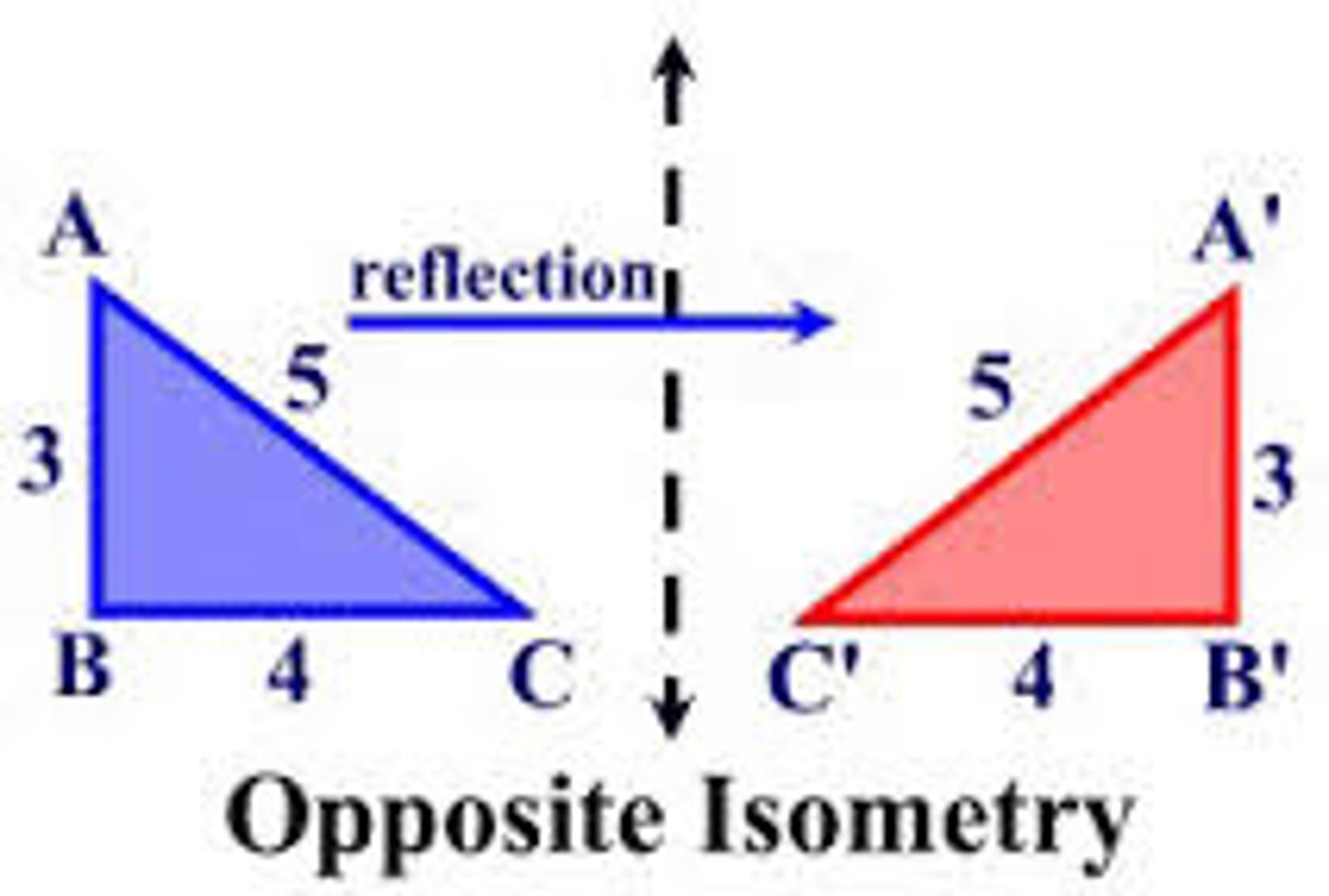
opposite transformation

a transformation that changes the orientation of a figure

polyhedron

a solid figure in which each face is a polygon

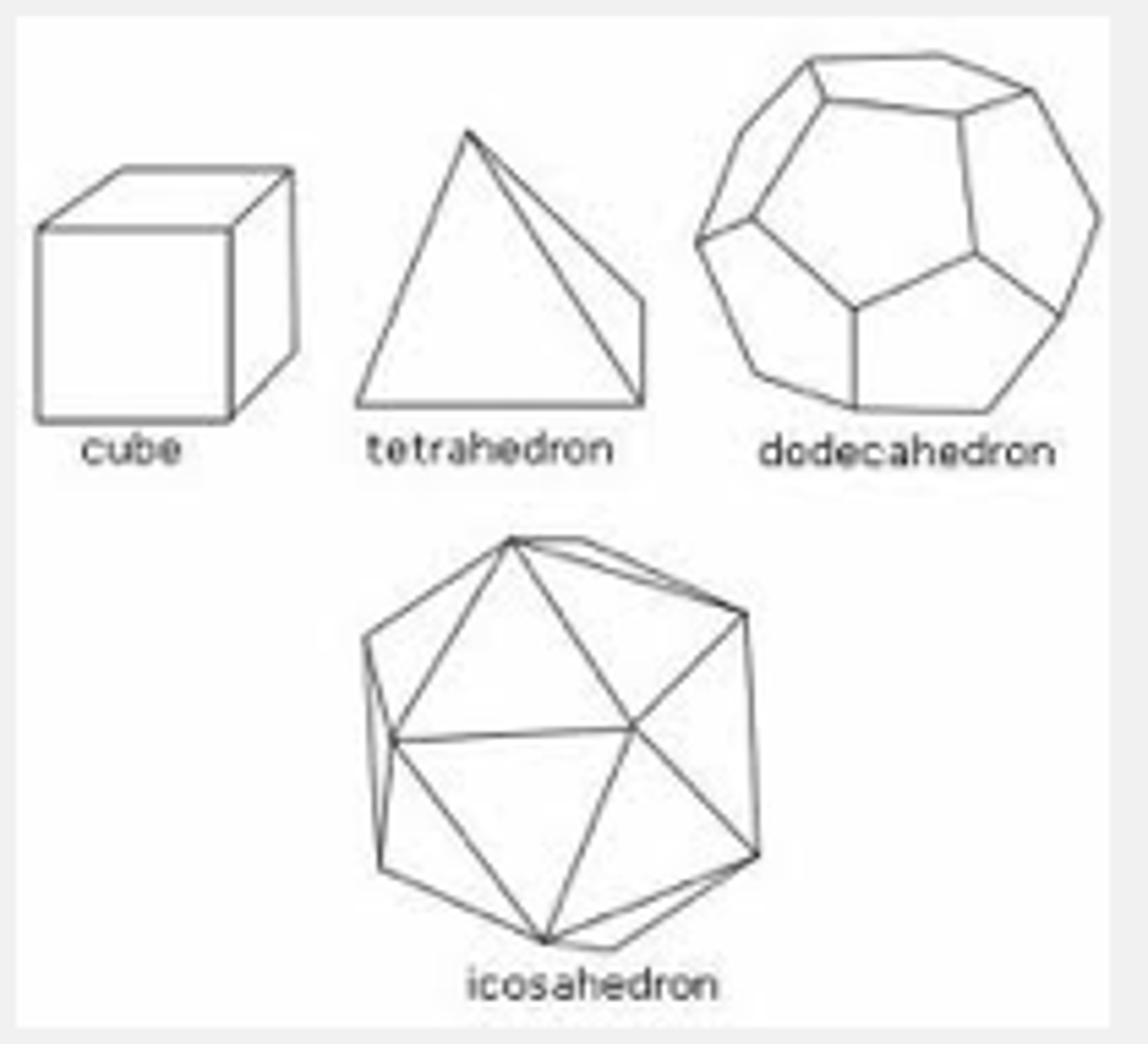
postulate

a statement that is accepted to be true without proof. EX: Subtraction postulate

right circular cone/cylinder

a cylinder/cone with a circular base and whose altitudes pass through the center of the base

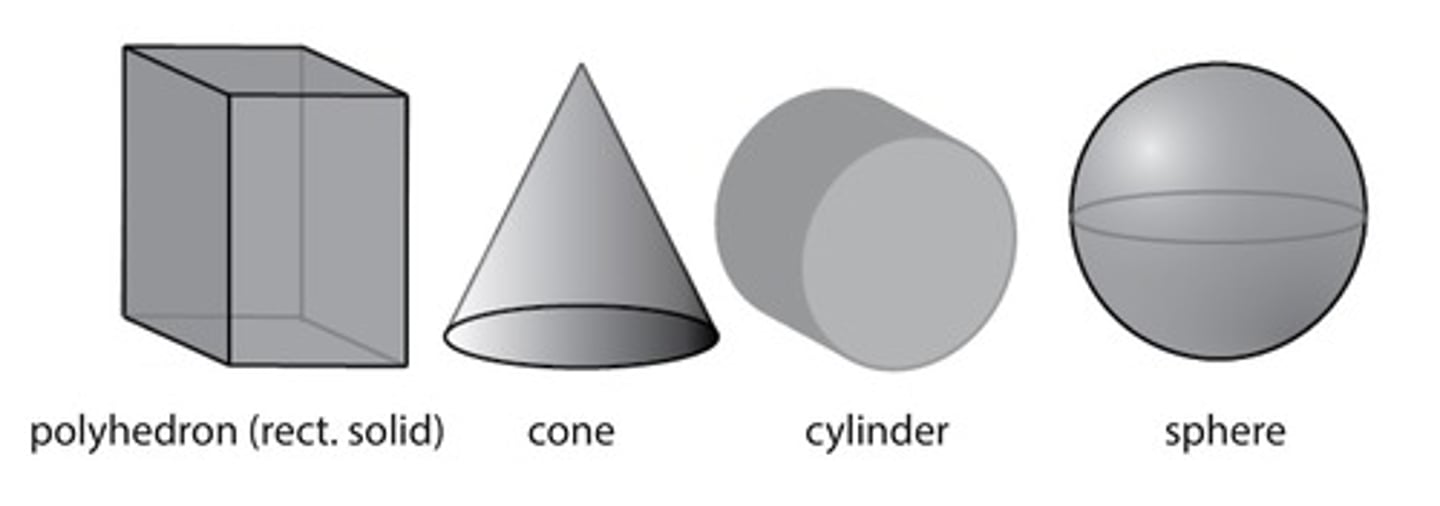
right pyramid

a pyramid whose faces are isosceles triangles

vector

a quantity that has both magnitude and direction; represented geometrically by a directed line segment. It's symbol is an arrow towards the right

intersecting chord theorem

a relation of the four line segments created by two intersecting chords in a circle. It states that the products of the lengths of the line segments on each chord are equal.

A dilation produces

parallel sides

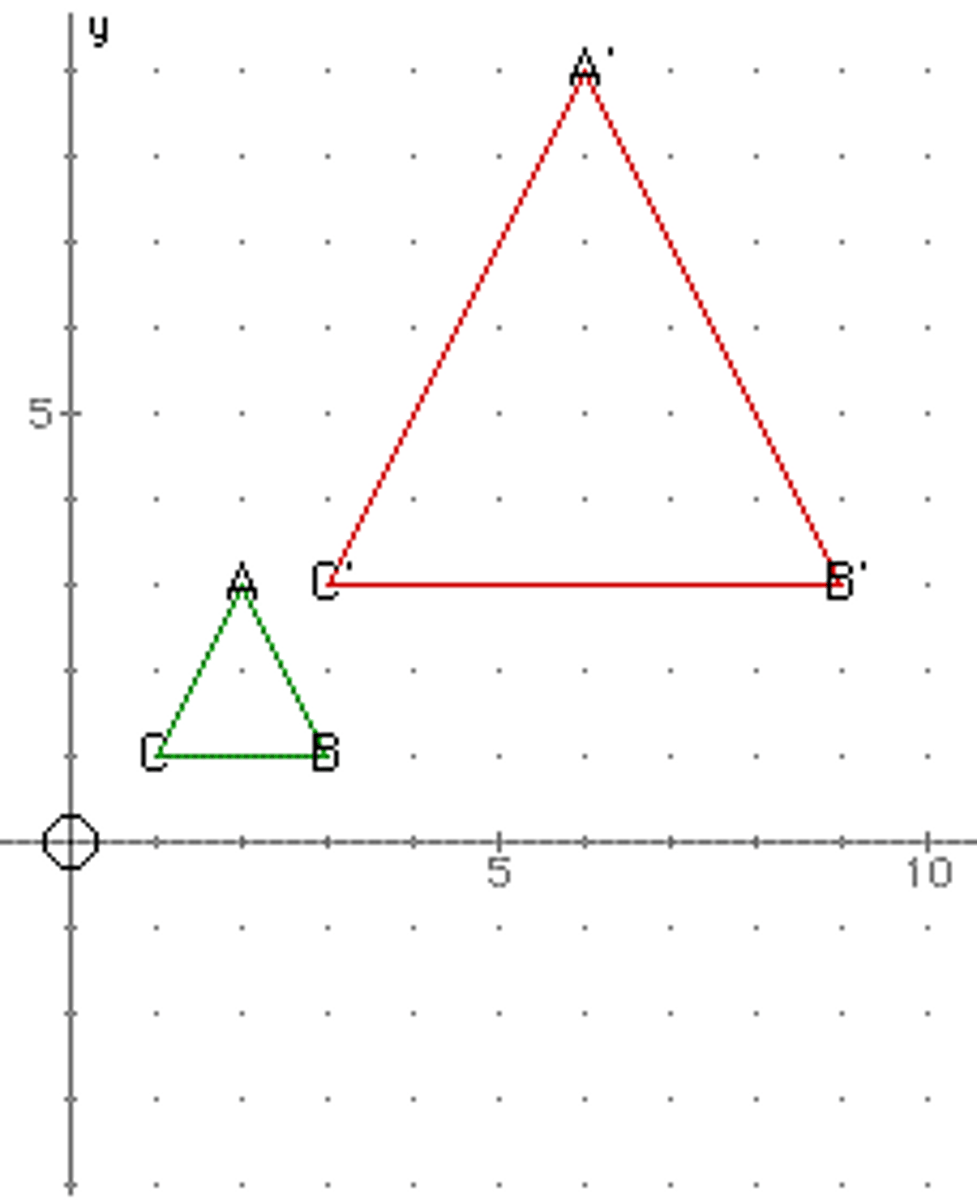
Dilations preserves

parallelism

point-slope formula

Y-Y1=M(X-X1)

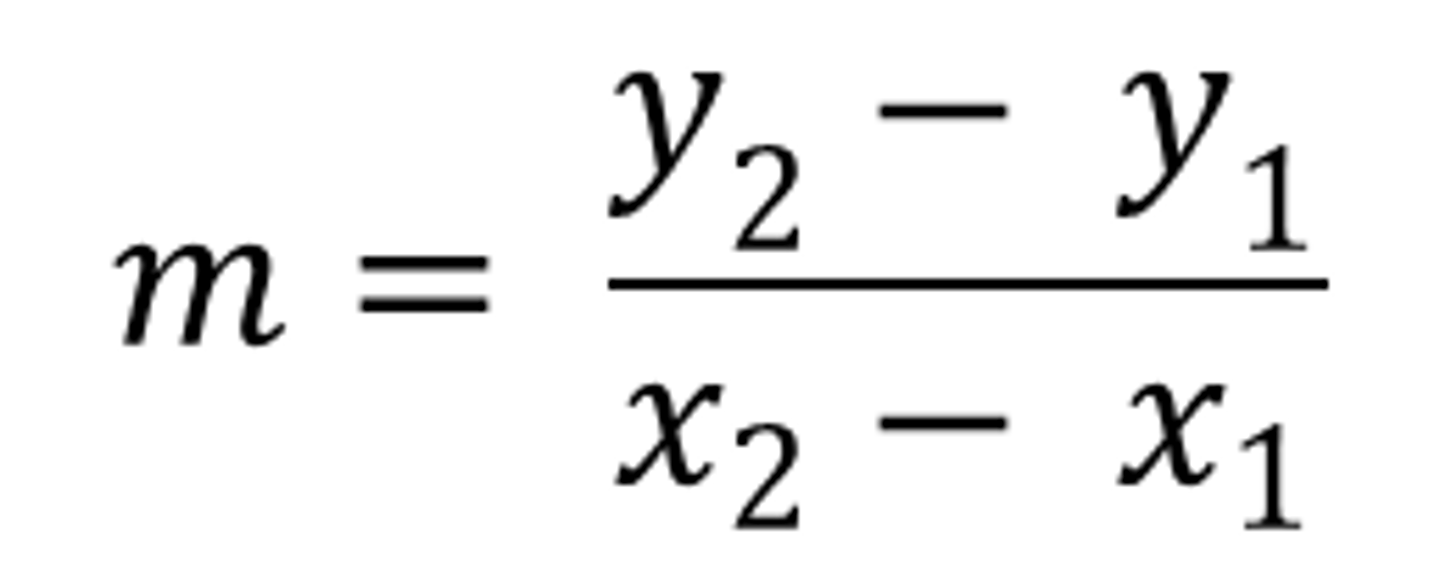
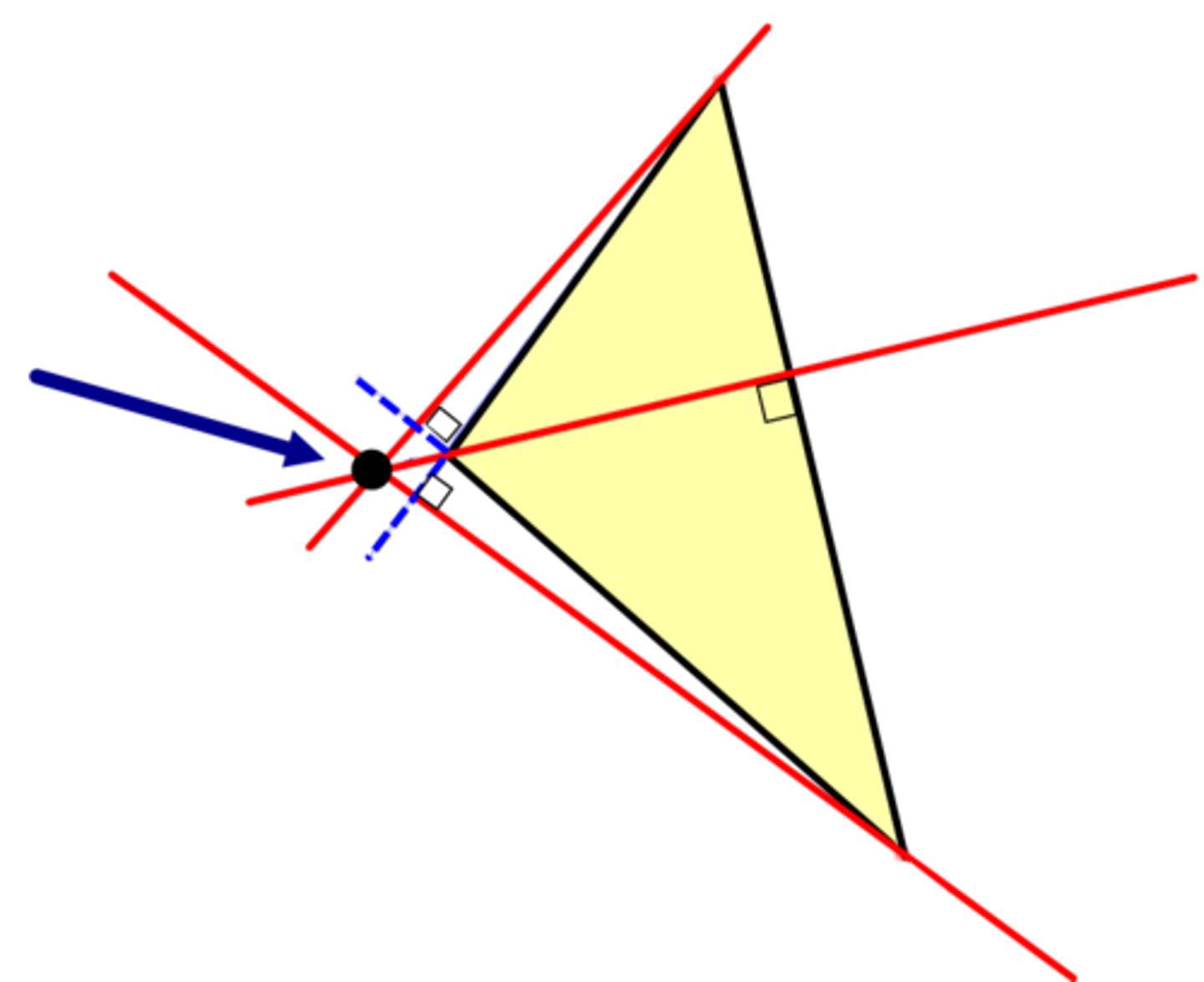
Of what triangle is it's orthocenter outside the triangle?

Obtuse triangle

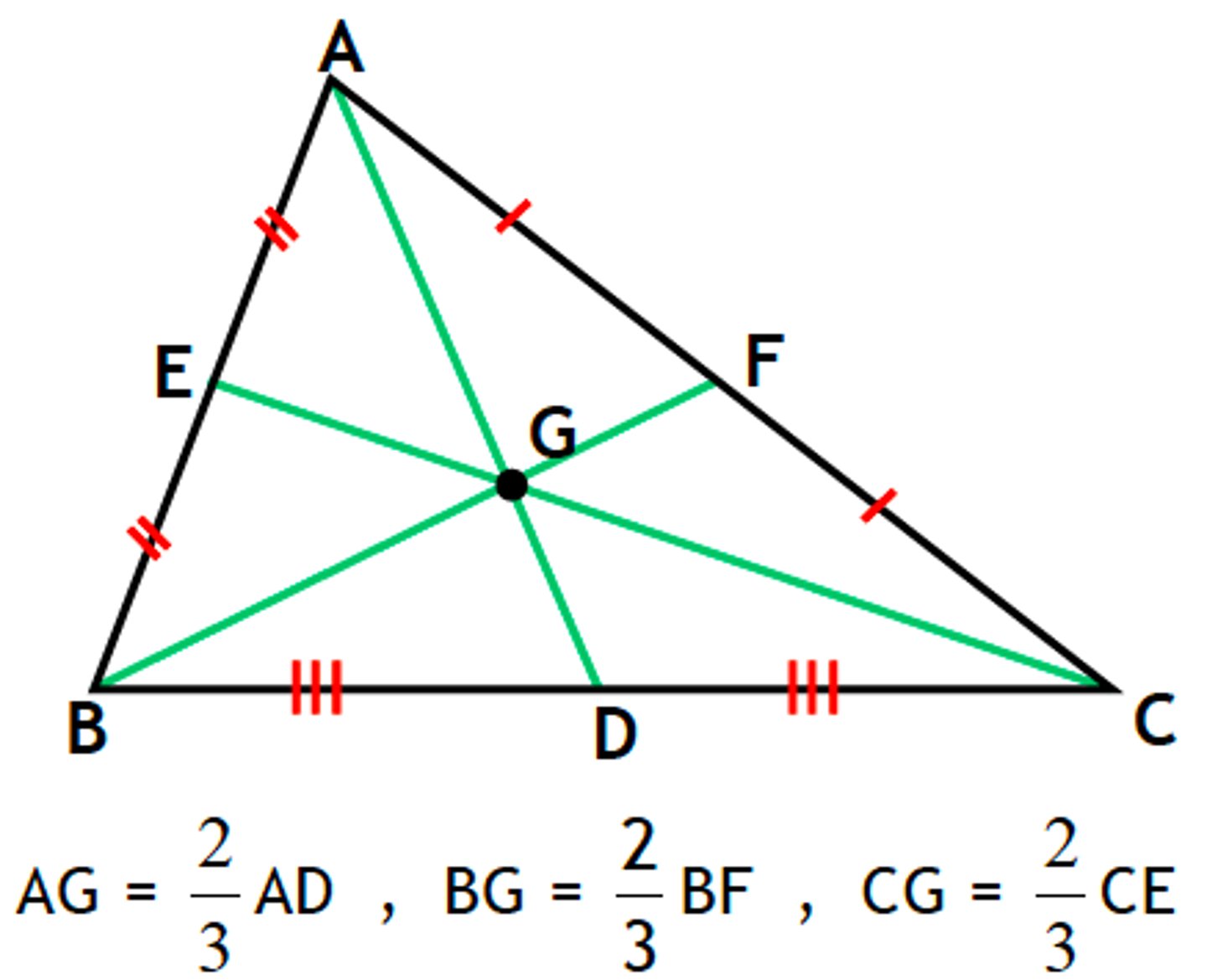
What does the centroid do?

It divides each median of the triangle into segments with a 2:1 ratio

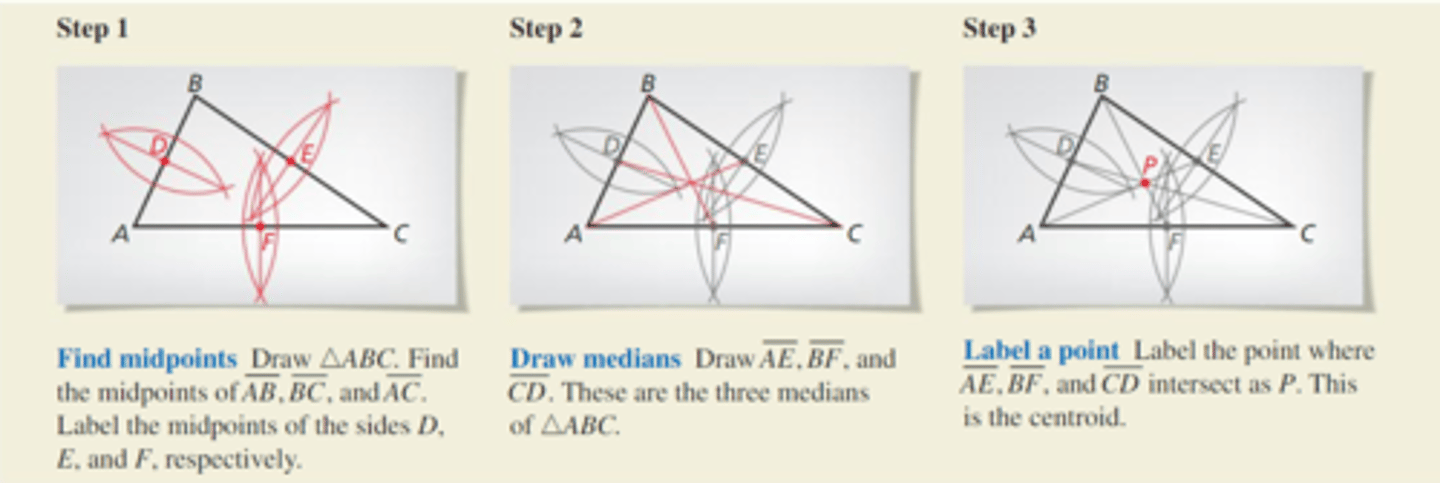
How do you find the centroid of a triangle?

By averaging the x coordinates (just the x) and the y coordinates (just the y) of all three vertices of the triangle

If two triangles are similar

their sides are in proportion

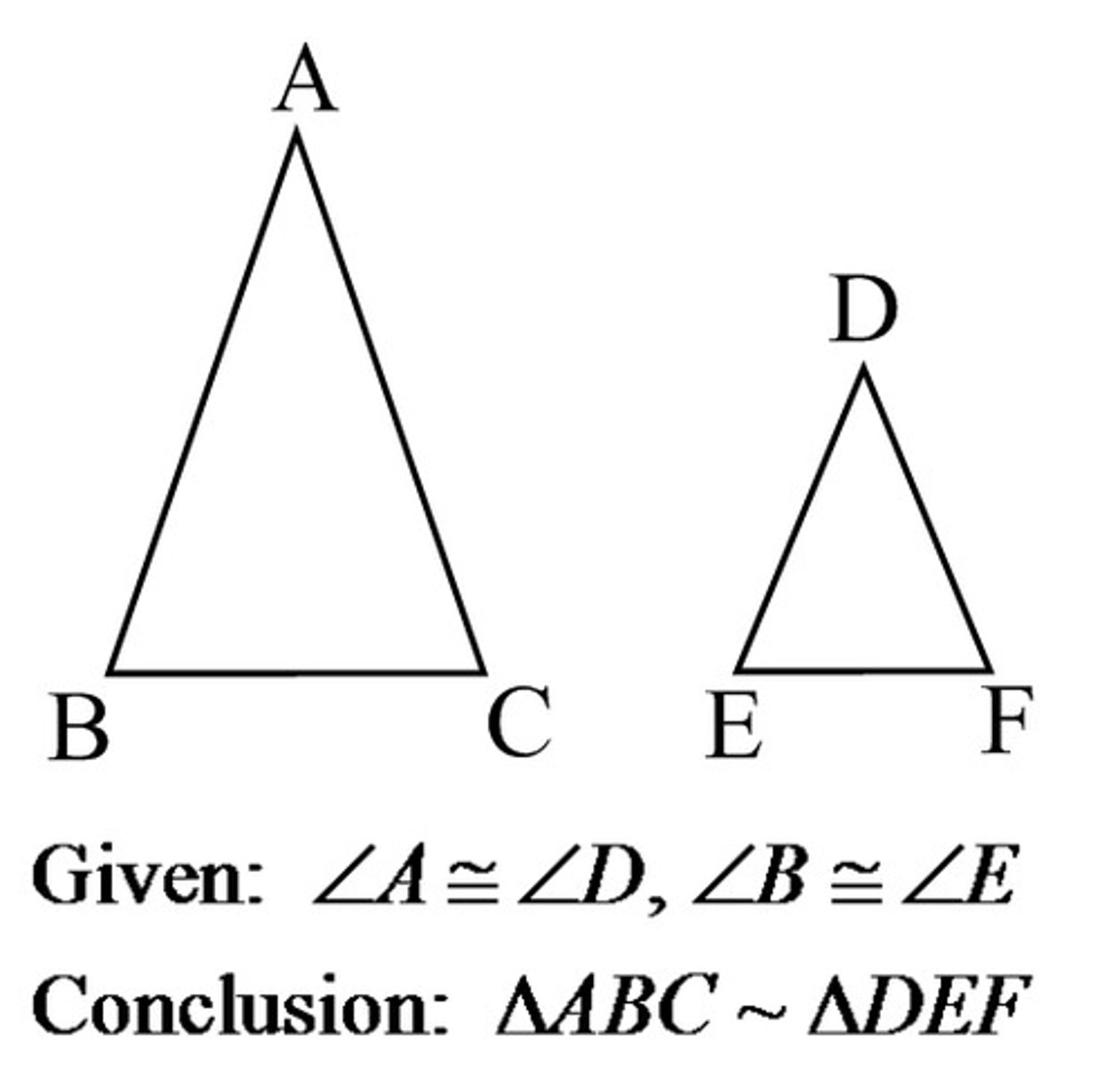
In a proportion, the product of the means...

is equal to the product of the extremes

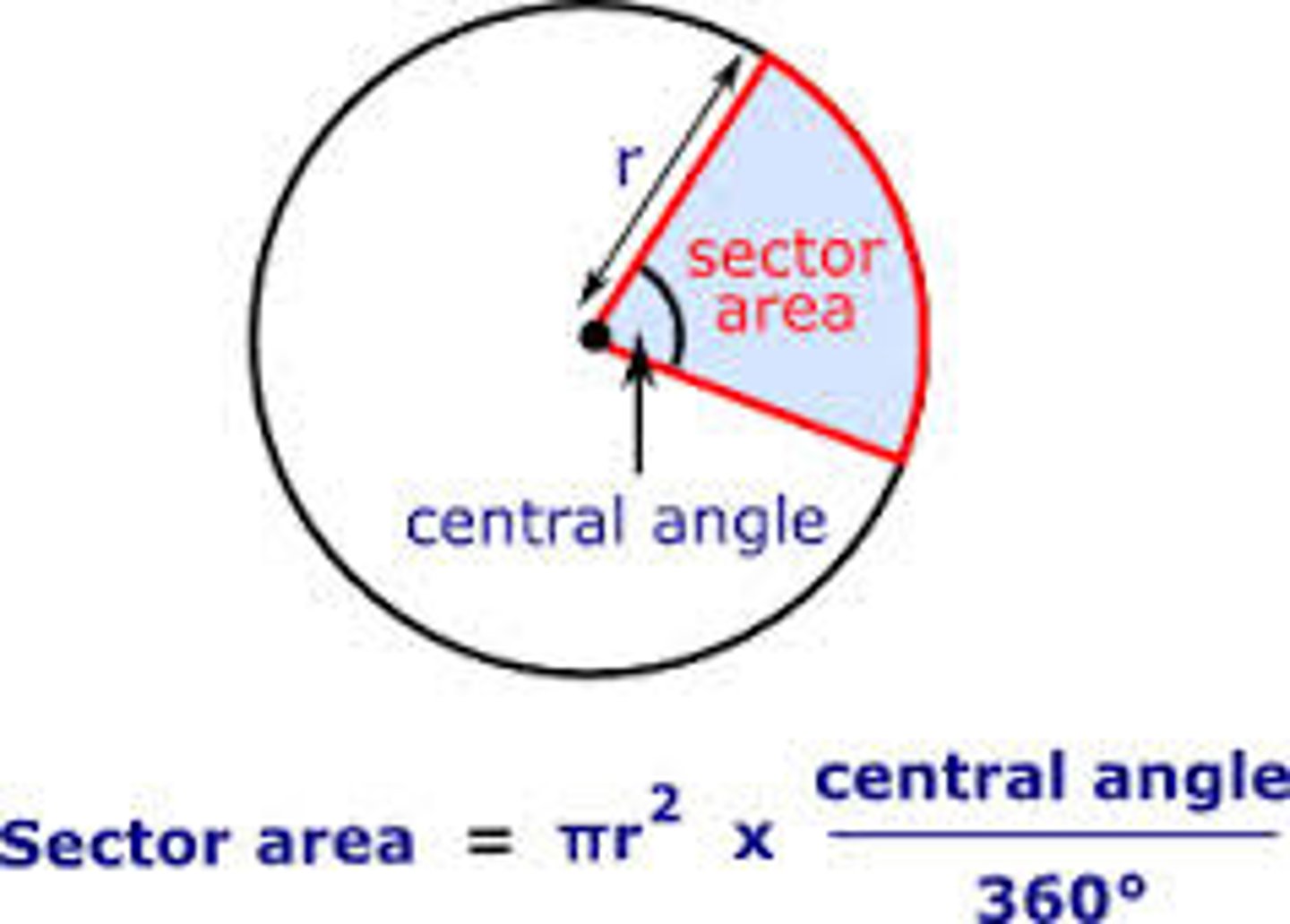
Sector area of a circle

((Measure of arc)/360) x pieRsquared

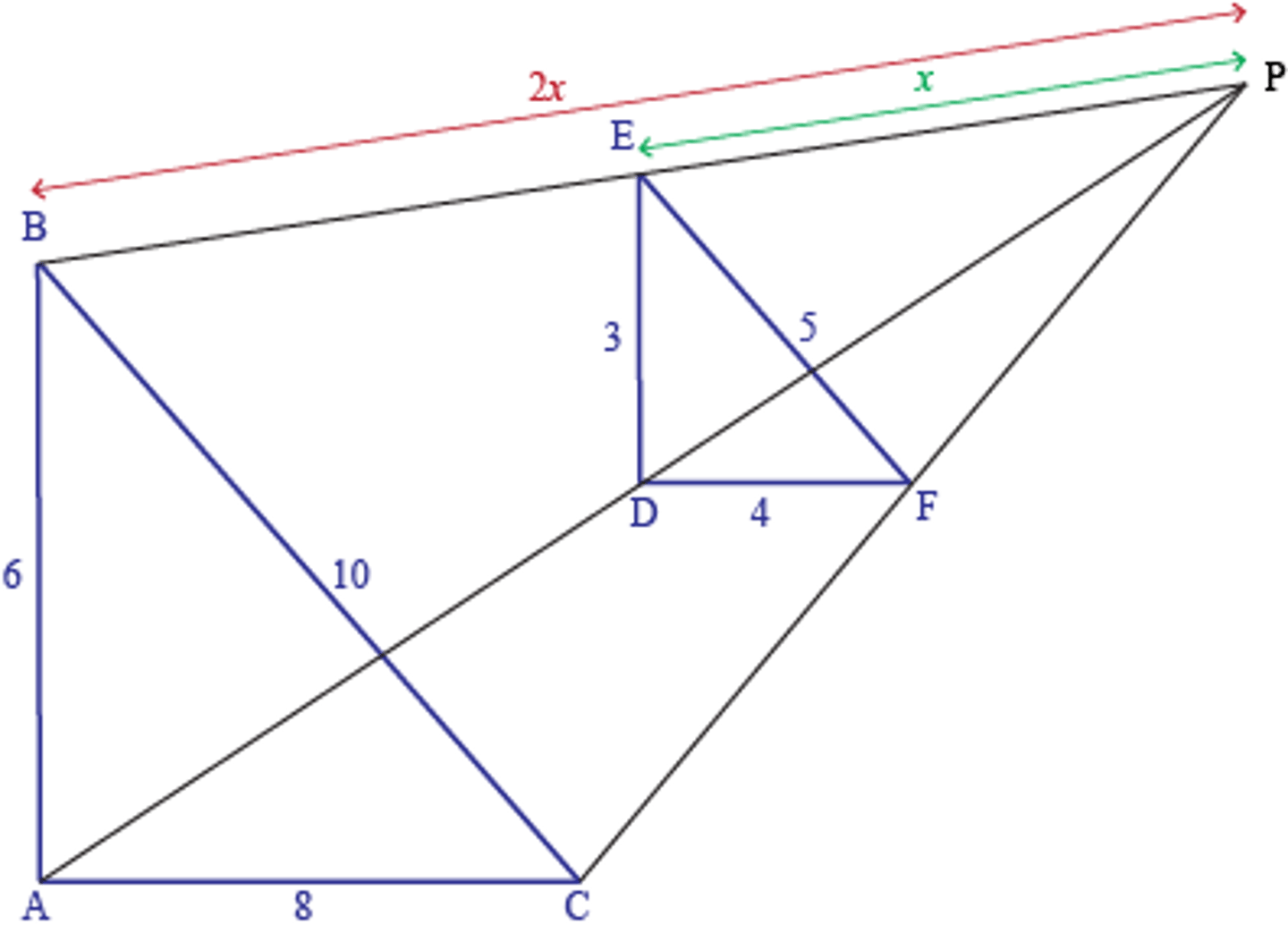
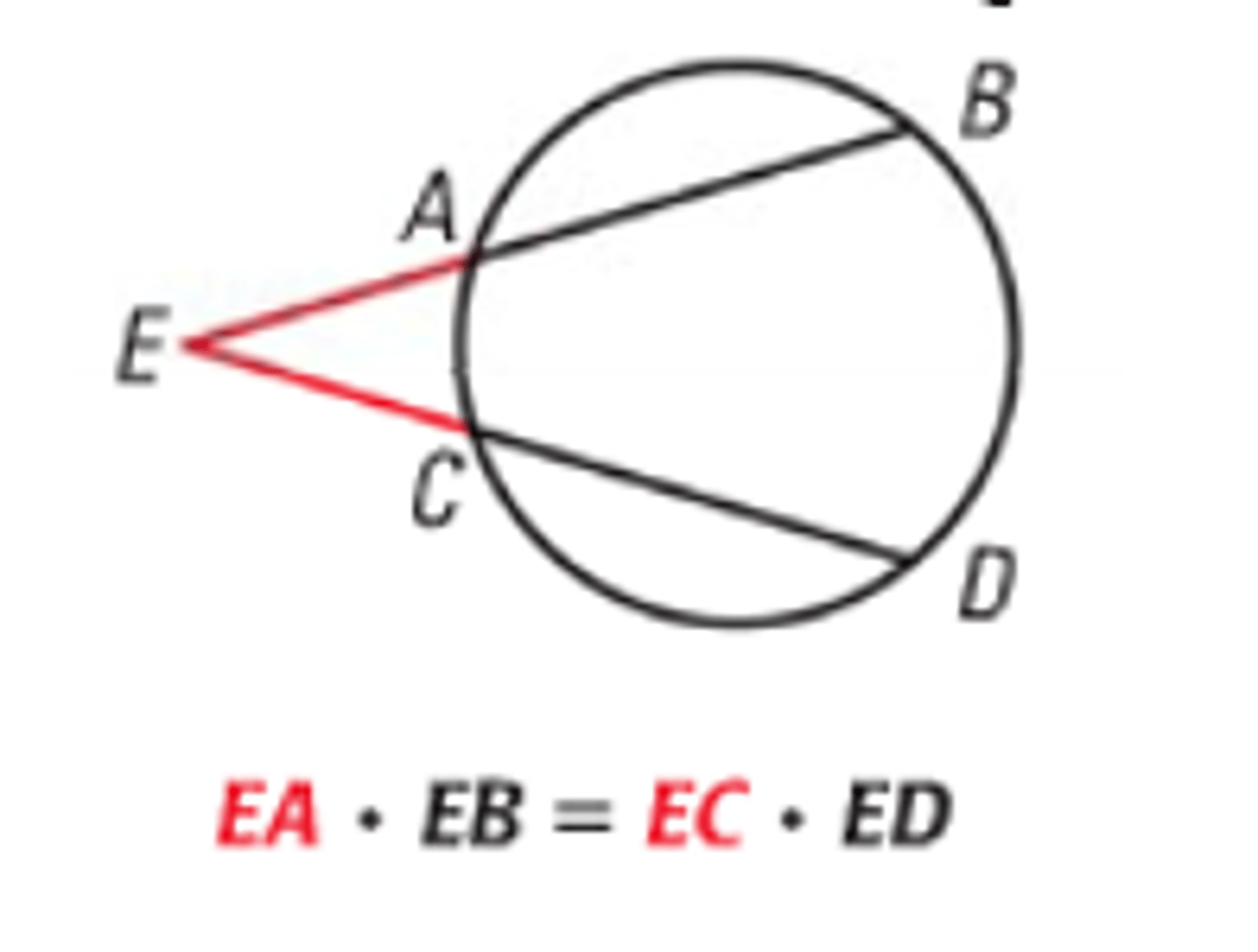
If you have two secants originating from the same point outside the circle, how do you solve for lengths of the secants?

WHOLExOUTER=WHOLExOUTER

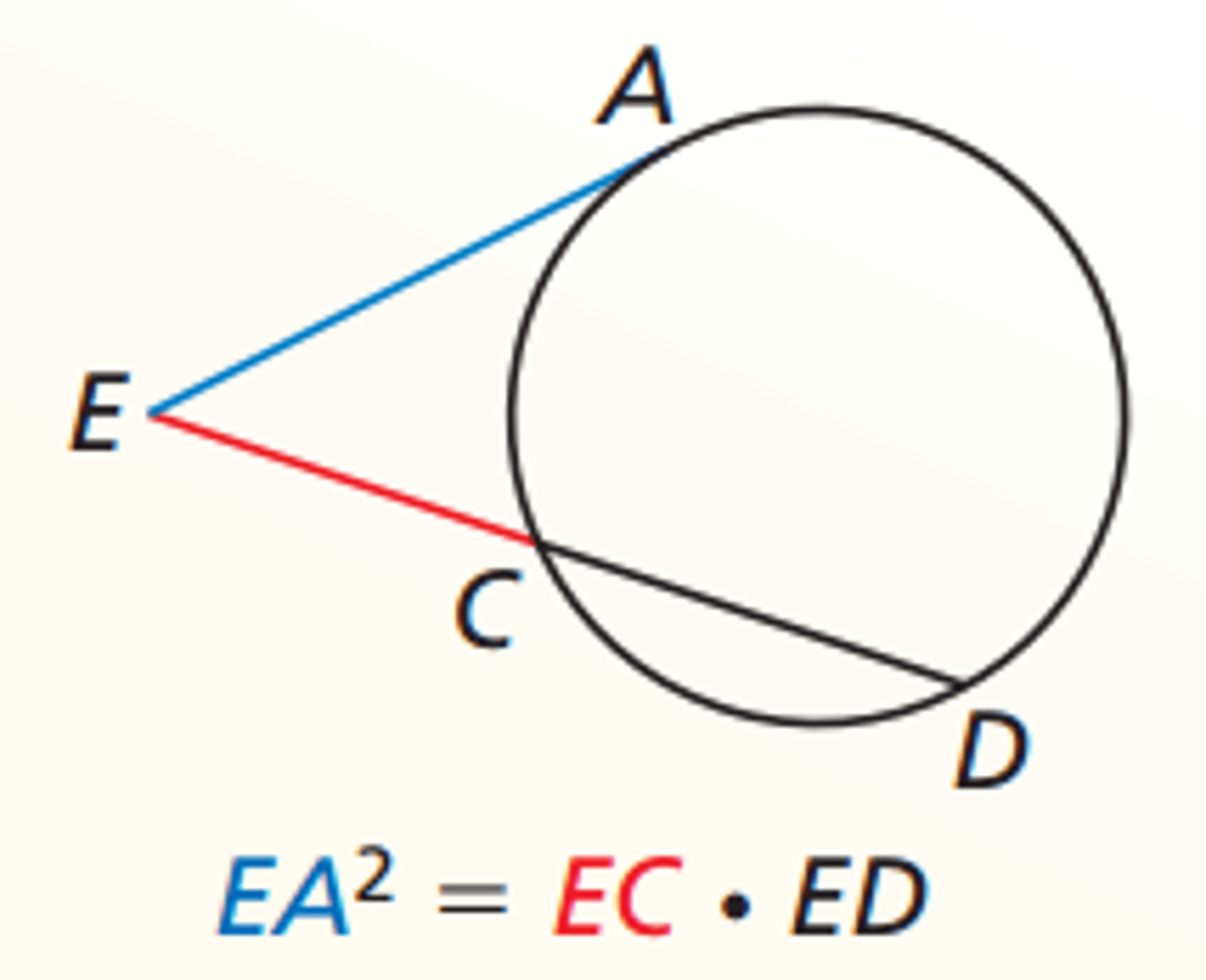
If you have one secant and one tangent that originate at the same point, How do you solve for the lengths of the line

Tangent length squared=Outer x Whole