Data Analysis

Descriptive statistic

• procedures for describing individual variables and relationships between variables

• eg. describing characteristics of study sample

Inferential statistics

• procedures used to analzye data after an experiment is completed

• procedures used to determine if an IV has a significant effect

• allow for the making of extrapolations from a sample to the population from which it was drawn

Three levels of measurement

• nominal

• ordinal

• ratio

  • 0 has a true value (can go above)

Nominal measurement

• involves no continuum

• assignment of numeric values is arbitrary

• discrete categories

Ordinal measurement

• implies underlying continuum

• values are ordered but intervals are not equal

  • community size

  • likert items etc

Ratio

• involves a continuum

• numeric values are assigned and reflect equal intervals

• 0 is a true 0

  • weight, age in years, etc

Tendency

• simple statistics that typify a set of values

• convey a sense of the data

  • Mean, median, mode

mean

• calculated by summing values and dividing by number of cases

• average

• used for ratio data

median

• calculated by ordering values then using the middle most value (mean of the two values if there are two middle values)

  • half cases will fall above the median and half will fall below

• ratio or ordinal data

mode

• most frequently occuring value

  • category of a variable with the most cases

  • used for ratio, ordinal and nominal data

dispersion

• the variability of measures

  • range

  • standard deviation

  • variance

Range

• subtracting the lowest score from the highest in a set of values

• can be described as indicating the highest and lowest values

Standard deviation

• reflects the average amount of deviation from the mean value in a set of values

• related to the normal distribution curve

• Sqrt of the sum of squares divided by N-1

Standard error of the mean

• the standard deviation relative to the sample size

Varience

• measure of SD squared

• this is a single number that represents the total amount of variate in a distribution

  • lots of this is not good

Standardizing data

• ensuring that units match up to allow for comparisons between units of different sizes

5 types of data standardization

• proportions

• percentages

• percentage change

• rates

• ratios

Proportions

• standard method of designating a portion of the total

  • 0-1 (none → all of the total)

  • can be used instead of percentages

  • Batting average is usually a proportion

Percentage

• proportion can be converted to this

• how often something happens per 100 times

Percentage change

• the amount tha tsomethign changes overa period of tiem

  • T2-T1/T1

Rates

• Represents the frequency of somthing for a standard sized unit

  • Eg. divorce suicide, crime rates

Ratios

• represent a comparison of one thing to another

• one thing over another

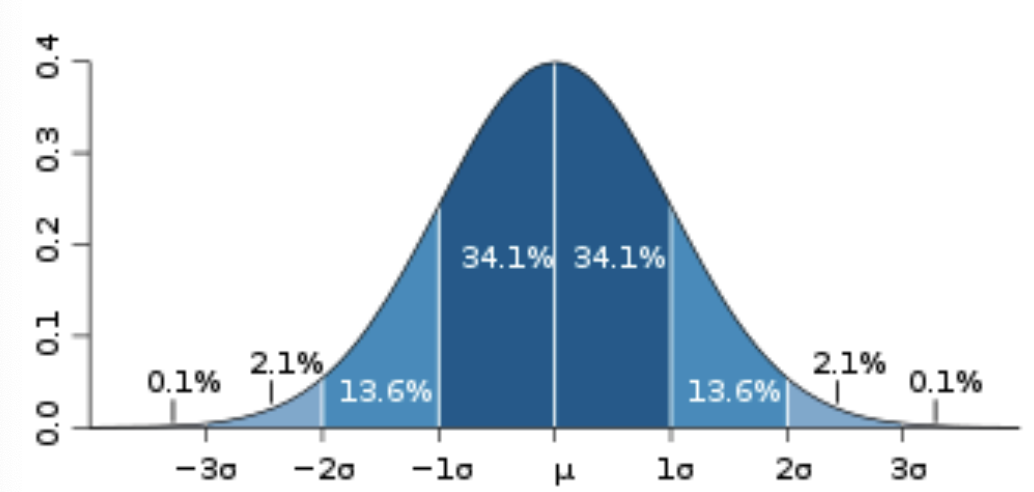
Normal distribution

• bell curve

• distribution pattern of a set of data follow this curve

• much data in the social and physical world is normally distributed

• symetrical will have half above and half below

Normal distribution and standard deviations

• 2/3 of cases are +- 1 sd of mean

• 95.6% of cases are +- 2 sd by definition

scores in 1 sd

• 68.2% will be within 1 sd to the right and left of the mean

z-scores

• standardized score

• represents the distance above or below the mean in standard deviation units of any raw value in a distribution

  • +3→-3 range in vlaues

Crosstabular analysis

• used with nominal DV

• data is cross classified and sorted into categories within the IV and DV to show relation between an IV and a DV

Comparing means

• when the DV is ratio and the IV is nominal or ordinal

• compare the mean values of the DV for each category of the IV

• both T-test and ANOVA can be used as tests of significance

  • comparisons of the means

Correlations

• used to describe the relationship between ratio level variables

• describes how close two ratio level variables co-vary together

• allows exploration

  • what is the equation describing the relationship between two variables

  • what is the strength of the relationships between two variables

equation for correlation

• y= a + bX

  • estimates how much the IV has to change to produce a unit of change in the DV

• a = constant

• b = slope

Regression line

• offers the best linear description of the relation between two variables

Correlation coefficient

• r demonstrates the strength of correlation between the two variables

• from -1 → +1

• -1 is a perfect negative correlation

  • an increase of 1 unit in one variable is associated with a proportional decrease in the other variable

• +1 is a perfect positive correlation

inferential statistics

• used to determine the probability that a conclusion based on an analysis of data from a sample is true and not due to sample fluctuations

Test of significance

• tests used to test a hypothesis

• chi square

• t-test

• anova

Hypothesis

• null hypothesis - prediction of no relationship between variables

  • this is what test of significance tests

• alternative research hypothesis - prediction of relationships

Testing the null hypothesis

• you either accept the null or reject the null

• to accpet the null it concludes that there is no difference between variables

• rejecting th enull concludes that there is probably a difference between the variables

Publication bias

• occurs if results from studies which have not been published are different than those that are published

• affects inerpretations of reviews and meta analysis that includes only publihsed literature

• favourable results are published more than non significant

Main effect

• differences among groups for a single independent variable that are significant temporarily ignoring all other independent variables

  • effect of the variable averaging over all variables in the experiment

interaction effects

• differences among groups of a single independent variable that are predictable only by knowing the level of the other independent variable

One tailed test

• indicates a direction of the relationship in advance

  • if you preduct the direction of a relationship inadvance you do a one tailed test

Two tailed test

• a test of any realtionship between variables

  • regardless of a direction of the relationship

Statistical significance

• degree of risk you are willing to make a type 1 error

  • rejecting null when it is true

Level of significance

• 0.05

• means there is a 5% chance of rejecting a true null hypothesis

  • less than 5% of the time the results that you are seeing wil be due to chance

statistical vs clinical significance

• statistical

  • gives probability of a relationship existing

  • nothing about the magnitude or importance of the difference

• clinical

  • the importance of the difference in the real world

    • this is determined by judgement

Statistical significance

• is a precondition for considering clinical importance but says nothign about the effect

Three tests of significance

• Chi-square test

• T- test

• ANOVA

  • extension of the T test

Chi-square test

• used with crosstabular analysis

• IV: Categorical - nominal or ordinal

• DV: Usually nominal

• Null: There is no significant difference between categories on the variable of interest

T-Test

• small sample sizes

• DV is measured at ratio level

• IV has two categorical levels only

• used to compare the means of two groups

• Null: No significant difference between group means on the DV of interest

Between subjects T-test

• two independent samples

• used in experimental design

• has an experimental and control group where the groups are independently established

Within subjects t-test

• in these designs, the same person is subjected to different treatments and a comparison is made between the two treatments

ANOVA

• family of tests that compares the group means to assess whether differences across means are reliable

• post hock: compares the differences across levels of an IV when results are significant

ANOVA conditions

• IV: 2+ categories

  • can be more than 1 IV at once

• DV: ratio level

• are there stat sig differences between groups on the characteristic of interest

  • how does the DV vary across categories of the IV

When are tests of significance not appropriate

• if the total population is studied then there is no need to determine stat sig

  • any observed difference is the absolute difference not a statistically significant difference

• Non-probability sampling procedures

  • if the sample was not random then results are more than likely not going to be significant

• Non-experimental research which is not intended to generalize

• High non-participation rates

  • if there are too many who do not participate it is hard to assume that those who do participate are similar to those who do not participate

• research without a formal hypothesis

  • if there is no hypothesis even if a relationship is found it is not significant

F statistic

• a higher F statistic there will be a lower p-value

  • higher F is more likely to be different

• Mean square determines F statistic

  • between group means /

    within group means

Degrees of freedom between groups

• subtract 1 from the total number of groups

Degrees of freedom within groups

• subtract the total number of groups from the number of observations

Degrees of freedom

• represents the number of individual fragments of information usd to calculate a statistic

  • the number of values in a calculation which are free to vary after constraints are imposed

Anova test statistic

• F ratio

• compares 2 estimates of variability

  • within and between group variability

• There is a sig difference when Vb is greater than Vw

  • this would show that the different conditions are resulting in different results on the DV

ANOVA limitation

• does not pinpoint where the difference occurs it only tells you if there are differences between any group in the study

  • post hoc tests are required to actually determine which groups are statistically different from another

Two-way ANOVA

• 2 simultaneous IVs of 2+ categories each (nominal or ordinal IV)

Post-Hoc analysis

• if significant main effect or interaction is foudn then you can conclude that there is a significant difference amongst the levels of your IVs somwehere

• Tukeys, Duncan (too liberal do not use)

Bivariate correlation

• how closely two ratio level variables co-vary together

Multiple regressions

• analysis of more than 2 ratio level variables

• used when we want to examine the impact of several IVs on a DV

• may be used when you have a ratio level DV and preferably ratio level IVs

• both bivariate correlations and multiple regression cannot prove causal relationships but they can provide evidence to support causal arguments

Multiple LINEAR regression

• simplest multiple regression

• considers the linear relationship among more than 2 variables

• isolates the seperate effects of IVs on the DV

• summarizes the relationship between a DV and 2+ IVS

3 m of data analysis

• model

• measurement

• method

Model

• determine whch variable is the DV and which will be the IVs

• possible that 2 variables mutually influence one another

• if possible specify in model > and < relationships between variables

Measurement of the.3 M approach

• identify the level of measurement

method of 3 m approach

• determine which method is appropriate for examining the relationships between variables

  • Crosstabs (chi-square)

  • means (ANOVA)

  • correlations