E1 Structure of the Atom

atom structure

E1.1 Rutherford’s gold foil

Studies alpha particle scattering. Beam of high E α particles fired at gold foil and detector on other side: nr of part + angle of refraction of α particles.
Some were

(1) reflected at >90^o ( small nr of part) - sug. small dense nucl

(2) transmitted straight line (majority) -suggest lotof empty space

(3) refracted at angle (θ <10^o) -suggest + central nucleus

This suggests: atoms consist of small, dense, + charge nuclei surrounded by negatively charged electron cloud.
Atom diameter: 10^-10m, nucleus diameter: 10^-15 m

E1.2 Nuclear Notation

All matter is made of atoms: proton + neutron + electron

can measure charge and mass in C/e/kg/u

Nucleus is described by: ^A_ZX notation (A=nucleon nr)(Z=prot nr)(X=chemical symbol of element)
A = Prot + neutr
Z = Prot (determines X)

E1.1 Rutherford’s gold foil

Studies alpha particle scattering. Beam of high E α particles fired at gold foil and detector on other side: nr of part + angle of refraction of α particles.
Some were

(1) reflected at >90^o ( small nr of part) - sug. small dense nucl

(2) transmitted straight line (majority) -suggest lotof empty space

(3) refracted at angle (θ <10^o) -suggest + central nucleus

This suggests: atoms consist of small, dense, + charge nuclei surrounded by negatively charged electron cloud.
Atom diameter: 10^-10m, nucleus diameter: 10^-15 m

E1.2 Nuclear Notation

All matter is made of atoms: proton + neutron + electron

can measure charge and mass in C/e/kg/u

Nucleus is described by: ^A_ZX notation (A=nucleon nr)(Z=prot nr)(X=chemical symbol of element)
A = Prot + neutr
Z = Prot (determines X)

E1.3 Atomic spectrum

When atoms emit/absorb light of certain wavelengths; emission and absorption. These provide evidence that electrons in atoms can only transition between discrete atomic energy levels.

Each element has its own spectra, can be used as a fingerprint.

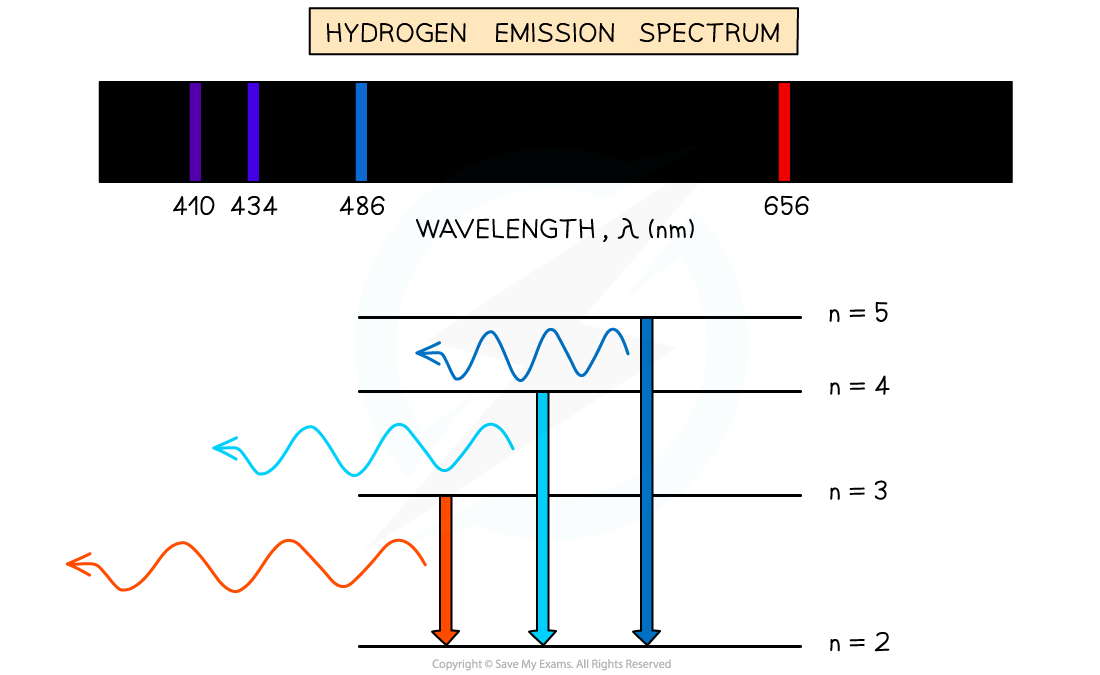
E1.4 Emission spectra

Produce by heating low-pressure gas. Excite e^- to higher E level

When they transition back to lower E level; emit photon

Each transition corresponds to specific wavelength of light → observable spectral line

Results in emission spectrium containing set of discrete wavelengths represented by coloured lines on black background

Eg. Hydrogen:

E1.5 Absorption Spectra

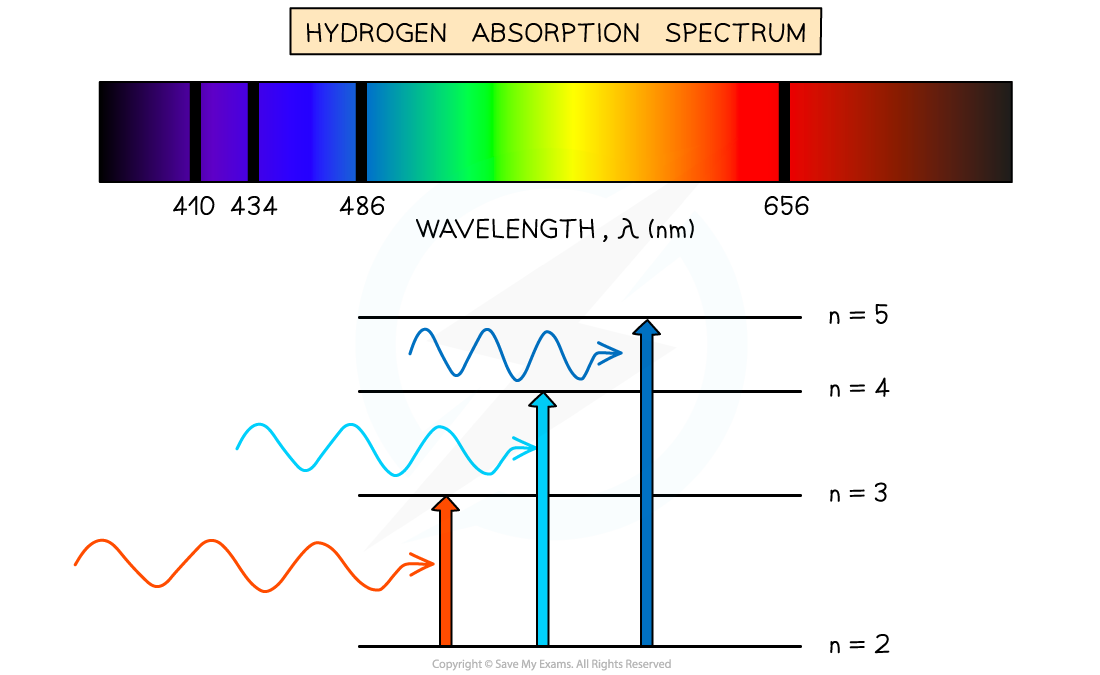
Cool, low pressure gas: only photons with exact E required to excite e^- will be absorbed.

Each absorbed photon → specific wavelength → dark line on continuous spectrum

Results in absorption spectrium containing discrete wavelengths represented by dark lines on coloured background → opposite of emission spectrum

E1.6 Photon Energy

Photon: massless packet/quantum of EM energy. → discrete/specific packet of energy, all transferred in 1 go.

E1.7 Atomic energy level

Electrons in atom occupy energy states → levels. Lowest possible energy level; most stable configuration. When e^- absorb/emit photon, moves between E levels or leaves atom completely.

E1.8 Exciting/Ionizing an electron + Energy photon

Excitation: when e^- moves up an E level; absorb photon, de-excite emits photon of exact same energy levels

Ionisation: when e^- is removed from atom.

Ionization energy: minimum energy required to remove an electron from ground state of atom

The energy of the emitted photon is equal to the difference in energy between the energy levels in the transition (high → low).

Energy of a photon E = hf = ^hc/_λ (h = 6.63 × 10^-34 Js)
If you look at diagram: up is absorbed, down is emitted (same E)

E1.9 Nuclear radius

Radius of nucleus depends on nucleon nr (prot+neutr) → experiment →

R = R_oA^1/3 (R₀ = 1.2×10^-15 m = Fermi radius; Hydrogen nucleus w 1 proton) (A = nucleon/mass nr = prot+neutr)

E1.10 Nuclear Density

V = ⁴/₃ πR³ = ⁴/₃ πR₀³A

m = Au (Nucleon nr, u=atomicmassunit (1.661×10^-27kg)

ρ = ^m/_V = nuclear density = ^u/(⁴/₃ πR₀³)

E1.12 Deviations of Rutherford scattering

He predicted that as scattering increases, nr of alpha particles at that angle decreases. However, at high energies of the alpha particles, this deviated → no back scattering → go to 0.

Rutherford assumed pure electrostatic repulsion, when in reality, at high E, they interact with nucleus via strong nuclear (force holding nucleons tg).

Therefore, Rutherford is also evidence for strong nuclear, by pushing alphas away

With smaller target nuclei (non gold) and higher energy alpha → more scattering as less effected by electric repulsion.

E1.13 Bohr Model (of Hydrogen)

Line spectra are drawn as to show different energy levels. electrons are able to jump/transition between these specific energy levels. These transitions are categorised into series;

Ground State: n=1 Lyman series (low wavelength → increas w n

E-levels ; Balmer → Ritz-Pashen → Brackett → Pfund

To n=2 produces visible light.

Bohr model of Hydrogen: e^- move in fixed orbits, restricted to certain radius.

Discrete energy of transitions in Bohr Model → E = -^13.6/_n² eV
E = photon energy, n = 1,2,3,4,5…. GIVE THIS IN…eV

E1.14 Bohr condition

^nh/_2π = mvr (v = v of e^-) (m=mass of e^-)(r=rad of orbit)(n=E-level)