Exam 2 Review

What is Statistical Inference?

Draw conclusions about population parameters using sample statistics

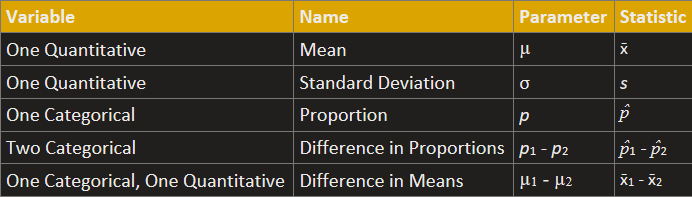
What is a parameter?

A measurement on a population

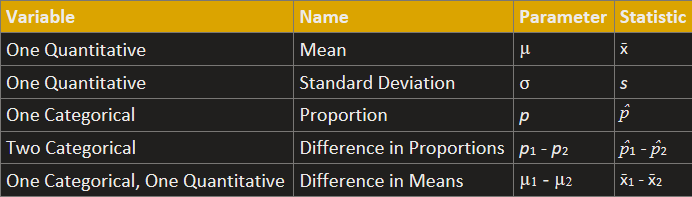
What is are two known facts about parameters?

1. They're fixed values

2. The values are often unknown

What is a statistic?

A measurement on a sample

What are two known facts about statistics?

1. They're known, or can be calculated once the sample is collected

2. Once a different sample is taken, it's most likely a diffrent value would be obtained (statistics vary from sample to sample)

If we need to identify the parameter we are conducting inference on, what two questions should we ask ourselves?

1. How many variables are being measured (one or two)?

2. What type of data do we have (categorical or quantitative)?

If we have one variable, the only parameters we could be doing inference on would be are what?

Mu or p

If we have one quantitative variable, we use what? (Hint from notes, mean gas price)

M (mu), the population mean

If we have one categorical variable, we use what? (Hint from notes, ESP)

P, the population proportion

If we have two variables that are both categorical, our parameter is the difference between population proportions, notated as what? (Hint, seatbelt use among teens and seniors)

p1 - p2

If we have two cateogrical groups measured using quantitative data, our parameter is the difference between populations means, notated as what? (Hint, word recal for nap and pill groups, or male and female height)

m1 - m2 (pronounced mu 1 - mu 2)

What is a Sampling Distribution?

The distribution of all statistics calculated from all samples of the same size, n, collected from a population. All samples must be collected randomly.

When should sampling distributions be constructed?

Only for two statistics, the sample mean and the sample proportion

Regarding the sampling distribution of the sample proportion, what is shape?

It depends on the size of the sample. With a large enough sample, the shape of the sampling distribution can be bell-shaped and symmetric

Regarding the sampling distribution of the sample proportion, what is center?

In all cases, the mean of the many, many p-hats is the population proportion, p

Regarding the sampling distribution of the sample proportion, what is spread?

As the sample size, n, increases, the standard error (standard deviation of the p-hats) decreases

Regarding the sampling distribution of the sample mean, what is shape?

It depends on the shape of the original population and/or the size of the sample. If the population being samples from is normal, then the sampling distribution will always be normal. If the population is not normal, but we have a large enough sample size (n > 30), the shape of the sampling distribution will also be bell-shaped and symmetric (approximately normal)

Regarding the sampling distribution of the sample mean, what is center?

In all cases, the mean of the many, many sample means (x-bars) is the mean population, m (or Mu)

Regarding the sampling distribution of the sample mean, what is spread?

As the sample size n, increases, the standard error (standard deviation of the x-bars) decreases

What is a confidence interval for a parameter?

An interval computed from sample data by a method that will capture the parameter for a specified proportion of all samples

What is a confidence interval for a statistic?

They supplement a statistic with an indication of the statistic's variability.

What question does a confidence interval answer?

"What is the value of the parameter?" This is a method of estimation.

Does a confidence interval make any claim or statement about the parameter?

No, no statement or claim is made about the parameter using a confidence interval

What two things do confidence intervals provide you with?

1. A range of plausible values for a population parameter

2. A confidence level, which expresses our level of confidence that the interval contains the population parameter

What do we know about confidence level interpretation?

We are 95% confident that the interval captures the true population parameter

In the long run, if we collected many, many samples and constructed many, many 95% confidence intervals, what would we capture?

95% of those confidence intervals will capture the unknown population parameter

How do we calculate the confidence interval?

CI: statistic +/- margin of error

True or False: The margin of error does not include the standard error in its calculation

False, the margin of error DOES include the standard deviation in its calculation

What is bootstrapping?

A method to estimate the standard error of a statistic without any knowledge of the population

True or False: Bootstrapping involves sampling without replacement from the original sample

False, bootstrapping involves sampling WITH replacement from the original sample

True or False: The size of a bootstrap sample will be the same size as the original sample

True, the bootstrap sample will be the SAME SIZE as the original sample

True or False: The center of the bootstrap distribution will be the standard deviation

False, the center of the bootstrap distribution will be the ORIGINAL STATISTIC

If we had a sample of size 6, how many samples would we take from the original sample using the "with replacement" strategy?

A. 12

B. 6

C. 24

D. 3

B. 6

Which of the following are true about bootstrap distributions?

A. The bootstrap distribution will be a collection of many, many bootstrap statistics

B. Most of these distributions are bell-shaped and symmetrical

C. The standard error is given with the bootstrap distribution

D. All of the above

D. All of the above

How do we calculate a 95% confidence interval (CI)?

95% CI: statistic +/- 2(SE)

How do we calculate a 90% or a 99% confidence interval (CI)

Using the percentile method in StatKey (right-tail and left-tail, or two tail)

True or False: As the confidence level increases (e.g. 90% to 95%), the width of the confidence level (CI) decreases

False, the width of the confidence level (CI) INCREASES with the rise of the confidence level

True or False: As the sample size of each sample increases (e.g. n = 50 to n = 500) the width of the CI will decrease (get more narrow)

True, the width of the confidence interval (CI) will DECREASE with the rise of the sample size

What is an hypothesis test?

An hypothesis test is used to judge or test between two different claims about the parameter

True or False: A claim is made about the parameter and a valuefor the parameter is stated in the null hypothesis,which is assumed to be false

False, a claim is made about the parameter and a valuefor the parameter is stated in the null hypothesis, which is assumed to be TRUE

True or False: An hypothesis test is a decision making process for evaluating claims about a staistic

False, an hypothesis test is a decision making process for evaluating claims about a POPULATION

What is the goal of an hypothesis test?

To assess evidence provided by the sample data to test a claim made about a population parameter

True or False: To accomplish an hypothesis test, you must compate the sample statistic obtained from a sample to a specific value claimed to be the sample statistic

False, to accomplish an hypothesis test, you must compate the sample statistic obtained from a sample to a specific value claimed to be the POPULATION PARAMETER

True or False: The true population parameter is a known quantity

False, the true population parameter is an UNKNOWN quantity

There are five steps in conducting an hypothesis test. What is the first step? (Hint, parameters of interest)

State the null and alternative hypotheses (it helps to state the parameters of interest)

There are five steps in conducting an hypothesis test. What is the second step? (Hint, what are we looking at?)

Find the observed sample statistic

There are five steps in conducting an hypothesis test. What is the third step? (Hint, randomization distribution)

Obtain the p-value (using the randomization distribution and H_a)

There are five steps in conducting an hypothesis test. What is the fourth step? (Hint, make a decision)

Make a generic decision about H₀: Reject H₀ or do not reject H₀

There are five steps in conducting an hypothesis test. What is the fifth, and final, step? (Hint, pretend you're writing an essay)

Make a conclusion in context, indicating whether or not we have convincing evidence for H_a and referring back to the question of interest

True or False: Just like bootstrapping, for each randomization sample in a randomization distribution, we calculate the parameter of interest

False, just like bootstrapping, for each randomization sample in a randomization distribution, we calculate the STATISTIC of interest

True or False: Many randomization statistics must be collected in order to generate a randomization distribution; this process must be repreated several times

True, many randomization statistics must be collected in order to generate a randomization distribution; this process MUST be repeated several times

What is true about the randomization distribution?

1. The randomization distribution will be centered at the value indicated by the null hypothesis

2. It shows what values of the sample statistic are likely to occur by random chance if the null hypothesis is true

True or False: The null hypothesis claims the effect we are looking for does exist

False, the null hypothesis claims the effect we are looking for does NOT exist. Also known as the no-change or no-difference hypothesis

True or False: The equal sign is always used in the null hypothesis

True, the equal sign is ALWAYS used in the null hypothesis

True or False: The alternative hypothesis says the claim we are looking for does exist

True, the alternative hypothesis says the claim we are looking for DOES exist (find the claim in the problem)

True or False: We believe the null hypothesis to be true throughout the calculation

True, we believe the null hypothesis to be TRUE throughout the calculation

What do we do after stating the hypotheses and generating a randomization distribution under the belief that the null hypotheiss is true?

Calculate the p-value

What is the p-value?

The proportion of samples that would give a statistic as extreme as (or more extreme than) the observed sample result, when the null hypothesis is true

The p-value gives us a way to numerically measure our surprise. What do smaller proportions mean?

Smaller proportions provide evidence AGAINST the null hypothesis, meaning we're very surprised

The p-value gives us a way to numerically measure our surprise. What do larger proportions mean?

Larger proportions provide NO evidence against the null, meaning we're not surprised at all

What are the steps for calculating the p-value?

1. Locate where the sample statistic lies in our randomization distribution

2. Determine what proportion of simulated statistics on the randomization distribution are as extreme as the observed statistic

True or False: The extreme of the p-value does not depends on the sign of the alternative hypothesis.

False, the extreme DOES depend on the sign of the alternative hypothesis

True or False: Sample statistics farther out on the tail of the randomization distribution give smaller p-values

True, Sample statistics farther out on the tail of the randomization distribution give SMALLER p-values.

In cases where the p-value is smaller, is it likely for the sample statistic to occur by chance alone?

No, in cases where the p-value is small, it is UNLIKELY for the sample statistic to have occured by chance alone

True or False: The smaller the p-value, the weaker the statistical evidence is against the null hypothesis and in support of the alternative hypothesis

False, the smaller the p-value, the STRONGER the statistical evidence is against the null hypothesis and in support of the alternative hypothesis

What is the decision rule for rejecting H₀?

If our p-value < a (alpha), then we REJECT H₀ (in favor of H_a)

What is the decision rule for not rejecting H₀?

If our p-value is > a (alpha), then we DO NOT REJECT H₀

What is a Type I Error?

A Type I Error occurs when we reject a true null hypothesis (also known as a false positive)

What is a Type II Error?

A Type II Error occurs when we do not reject a false null hypothesis (also known as a false negative)

True or False: A two-tailed hypothesis test using the significance level "a (alpha)" does not reject the null hypothesis exactly when the value stated in the null hypothesis is not captured by "a (alpha)" (1 - a) confidence interval

False, A two-tailed hypothesis test using the significance level "a (alpha)" REJECTS the null hypothesis exactly when the value stated in the null hypothesis is not captured by "a (alpha)" (1 - a) confidence interval

In regards to a two-tailed hypothesis test, if a 95% confidence interval (CI) does NOT capture the parameter stated in the null hypothesis (H₀), then what should happen?

A two-tailed hypothesis test should reject H₀ at a 5% significance level

In regards to a two-tailed hypothesis test, if a 95% CI DOES capture the parameter stated in the null hypothesis (H₀), then what should happen?

A two-tailed hypothesis test should not reject H₀ at a 5% significance level