Van Der Waals Interaction

Stable Equilibrium in Molecules

In a molecule, two atoms reach a stable equilibrium when the attractive and repulsive forces between them balance. At this point, the net force is zero, and the atoms can oscillate slightly around this position.

Attractive Force Between Atoms

When two neutral atoms are separated by a few atomic diameters, they experience a weak attractive force due to the temporary polarization of their electron clouds, drawing them together.

Repulsive Force Between Atoms

When atoms get very close, their electron shells overlap, creating a strong repulsive force that prevents them from collapsing into each other.

van der Waals Interaction

A weak attraction between neutral atoms or molecules caused by temporary shifts in electron distribution, leading to induced dipoles. It helps form molecular bonds at certain distances.

Lennard-Jones 6-12 Potential

A mathematical model describing the potential energy between two neutral atoms.

U(x) = 4ε[(σ/x)^12 - (σ/x)^6]

Lennard-Jones 6-12 Potential

Repulsion (when atoms are too close)

What does the first term of the Lennard-Jones 6-12 Potential equation represent?

Attraction (when atoms are farther apart)

What does the second term of the Lennard-Jones 6-12 Potential equation represent?

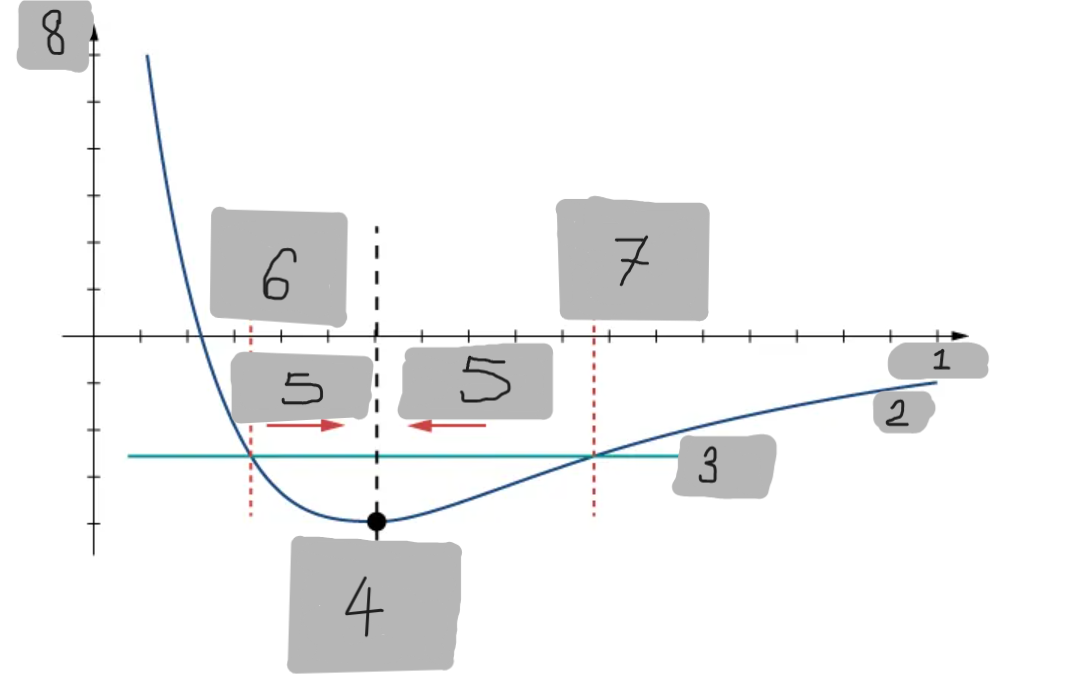
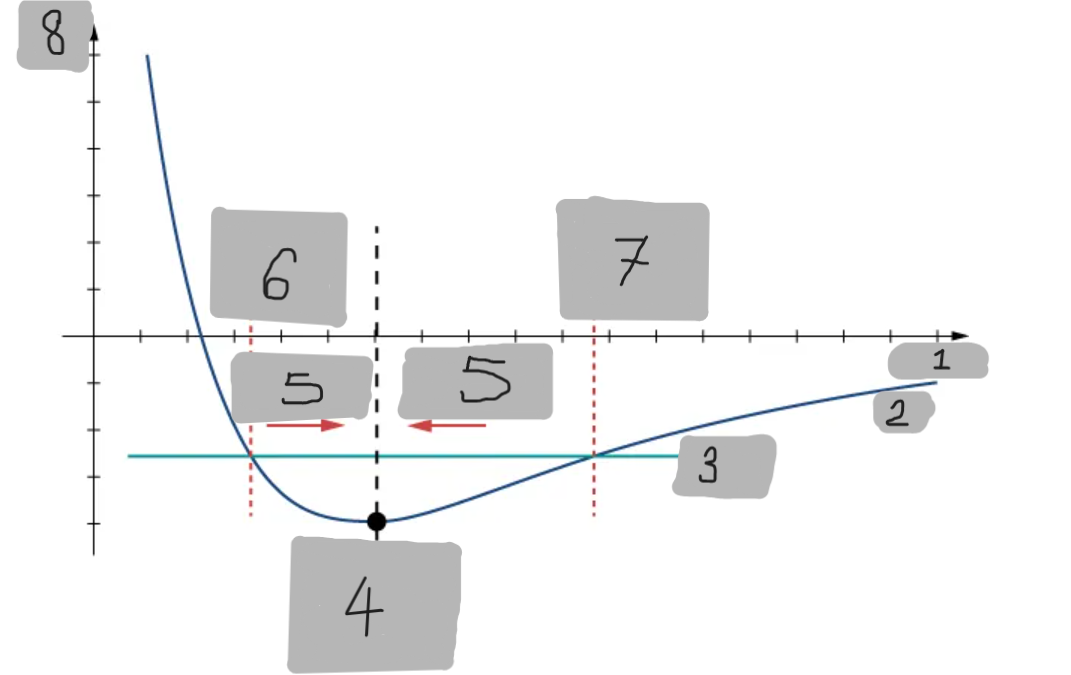
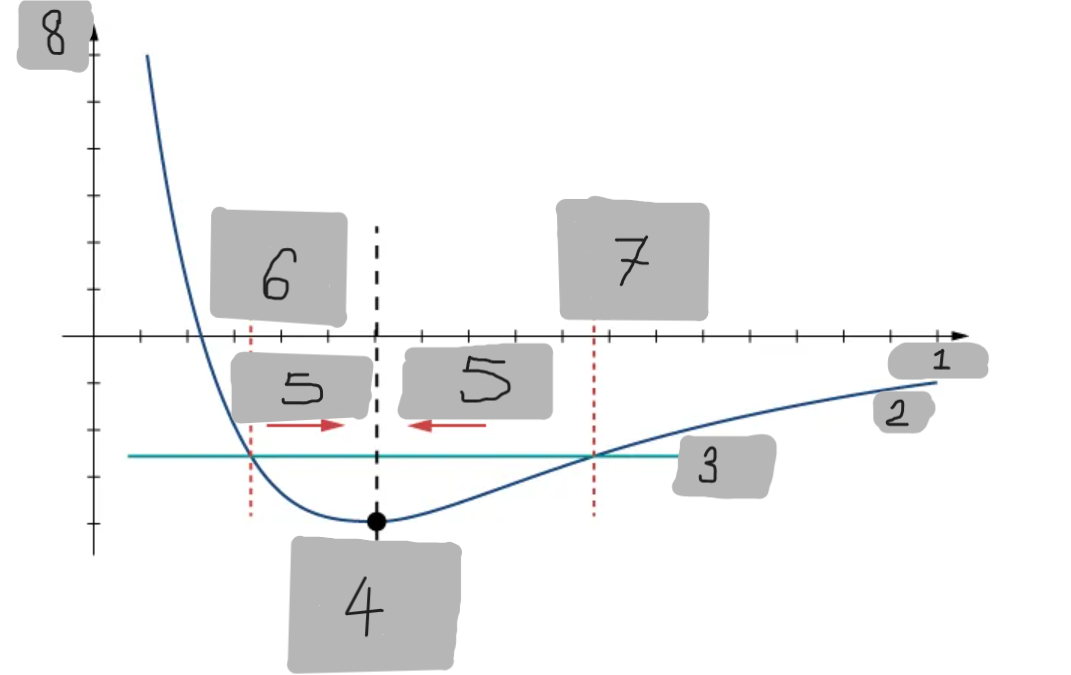
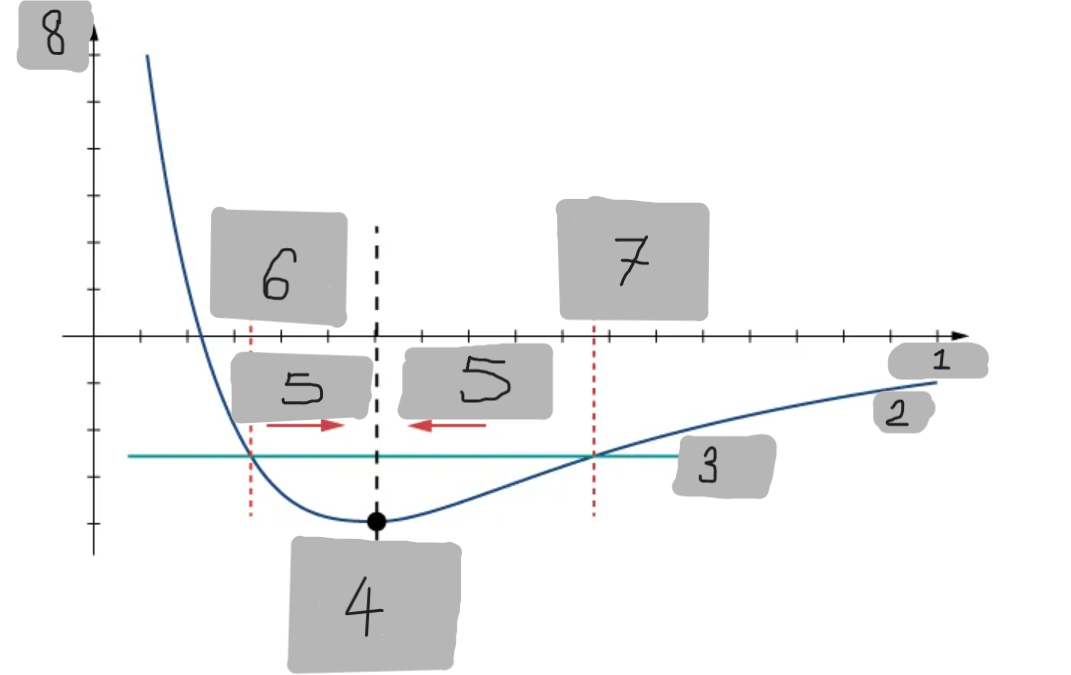
Potential Energy Well

The region around the equilibrium position in the Lennard-Jones curve where the potential energy is minimum. Atoms trapped in this well can oscillate around the equilibrium point.

Asymmetry of Lennard-Jones Potential

Unlike a simple harmonic oscillator, the Lennard-Jones potential is not symmetric because the repulsive force increases much faster as atoms get closer than the attractive force decreases as they move apart.

Force from Lennard-Jones Potential

• The force is the negative derivative of the potential F = -dU/dx

• It is not linear and does not follow Hooke’s law.

• However, near the equilibrium position, it can be approximated by a spring-like force F ≈ −kx

Hooke’s Law Approximation

For small oscillations near equilibrium, the Lennard-Jones force behaves almost linearly, allowing it to be approximated as F=−kx, similar to a harmonic oscillator.

Binomial Theorem (in Approximation)

A mathematical expansion used to approximate complex terms in the potential energy equation. It helps simplify the Lennard-Jones force near equilibrium to resemble Hooke’s law.

x(m)

(1)

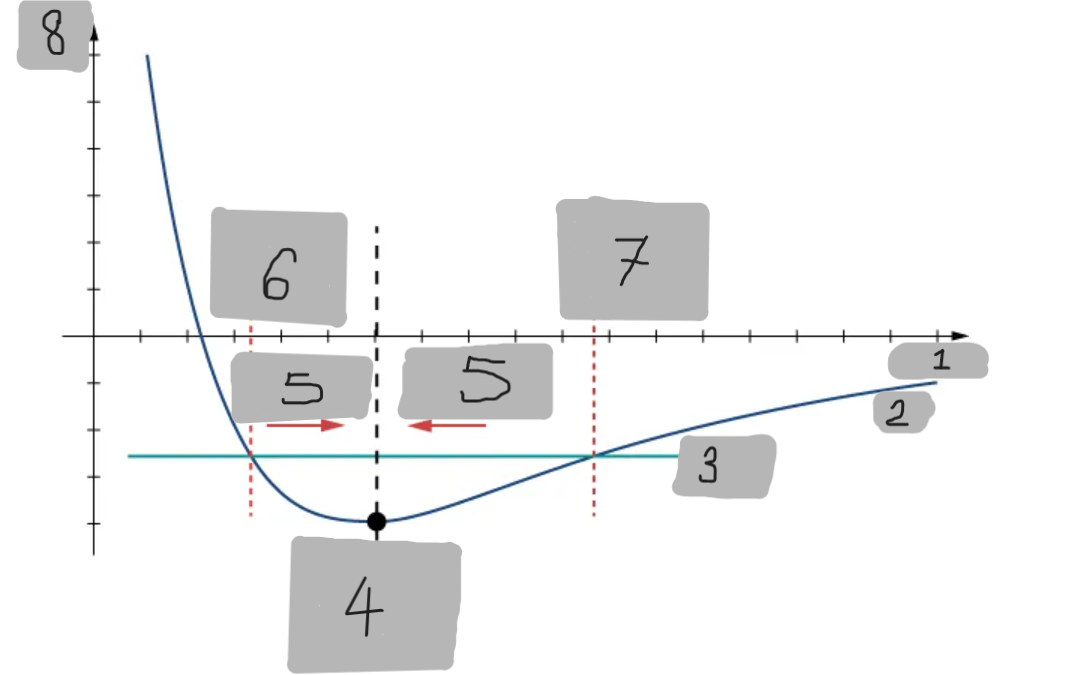
U

(2)

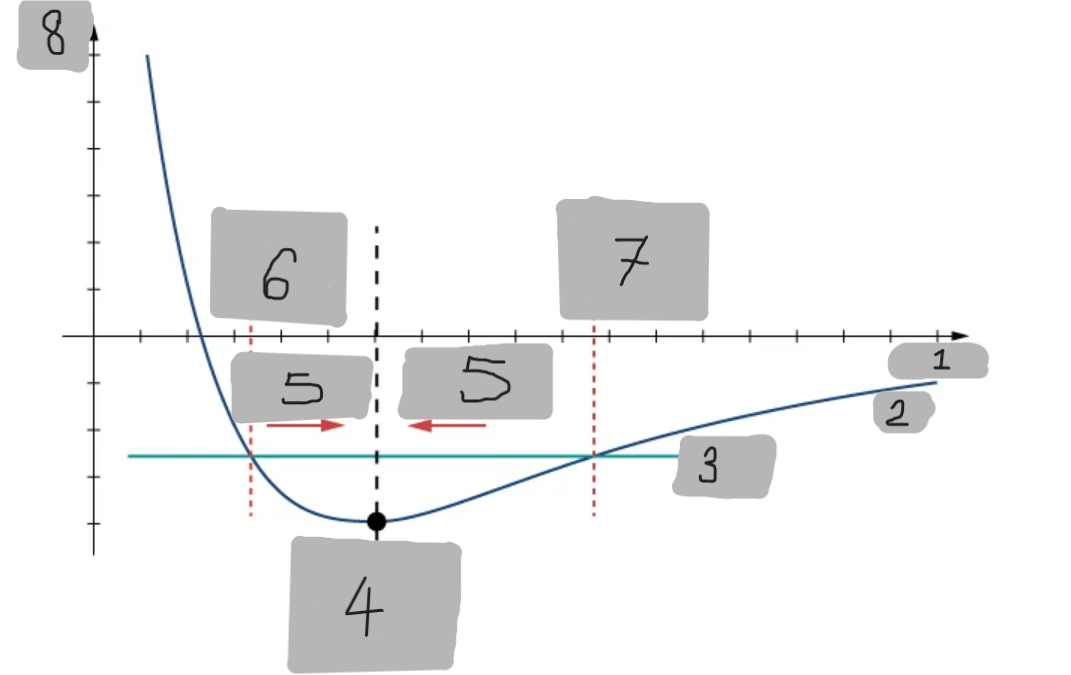
Etotal

(3)

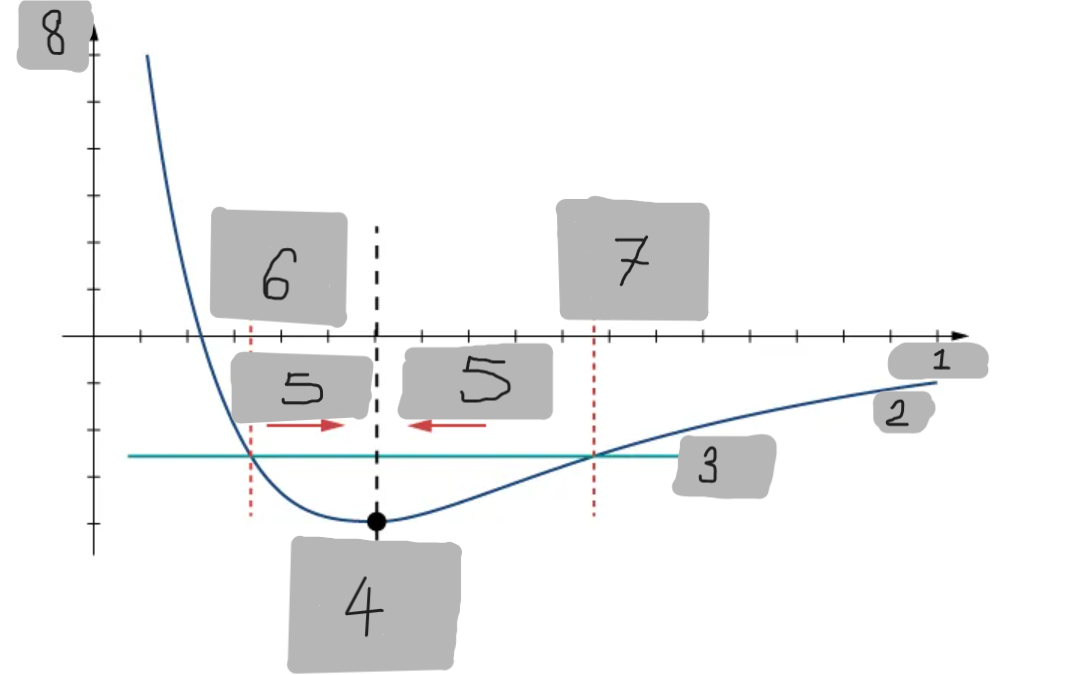
Equilibrium position F = 0

(4)

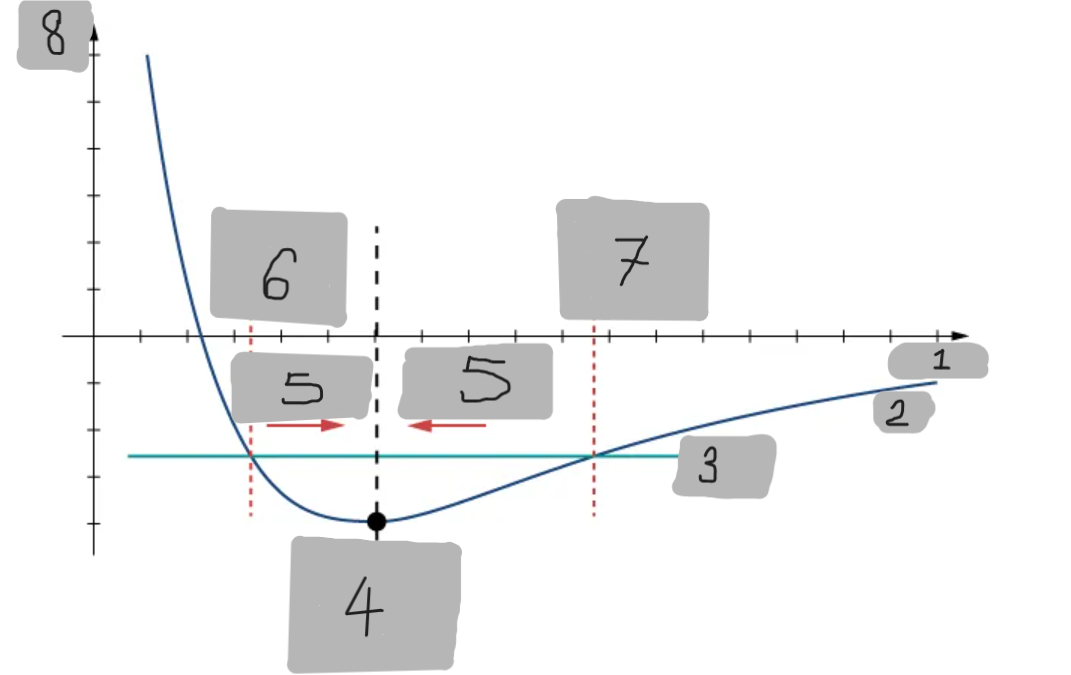
F = -(dU/dx)

(5)

Turning point A1

(6)

Turning point A2

(7)

E(J)

(8)

Etotal = ((1/2)k(x^2)) + ((1/2)m(v^2)) = (1/2)k(A^2)

Equation for the Total Mechanical Energy in SHM

U = (1/2)k(x^2)

Equation for the Potential Energy inside the spring

K = (1/2)m(v^2) = (1/2)k((A^2) - (x^2))

Equation for Kinetic Energy in SHM

|v| = ((k/m)(A^2 - x^2))^1/2

Equation for the magnitude of the velocity at any position in SHM

E ∝ A^2

The total energy of a simple harmonic oscillator is proportional to the square of its amplitude

quadruples

In an SHM doubling the amplitude __________ the total energy of oscillation.

By considering the uniform circular motion.

What is an easy way to model an SHM?