2.3.3 sorting algorithms

big 0 cheat sheet

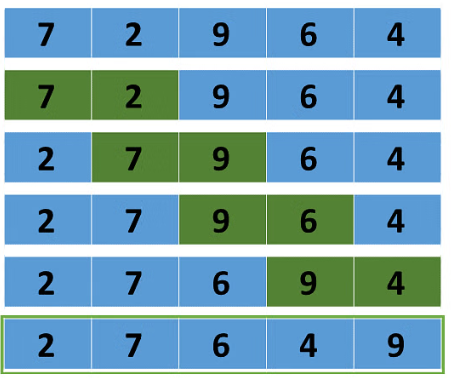
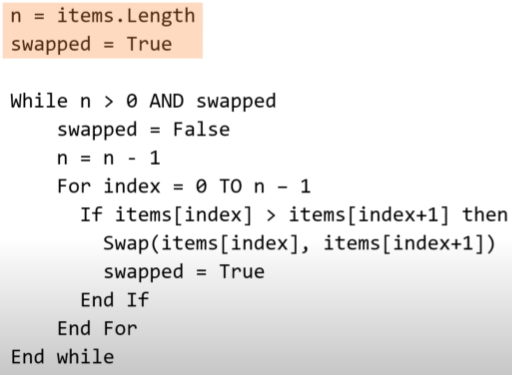
how does a bubble sort work

• start at the beginning of the list

• compare the current item with the next one

• swap if they’re in the wrong order

• repeat until the largest item "bubbles up" to the end

• repeat the process for the remaining unsorted part

bubble sort complexities

• time = O(n²)

• space O(1)

• inefficient but easy to implement, so good for small data sets

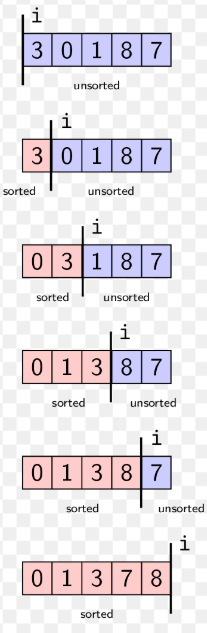
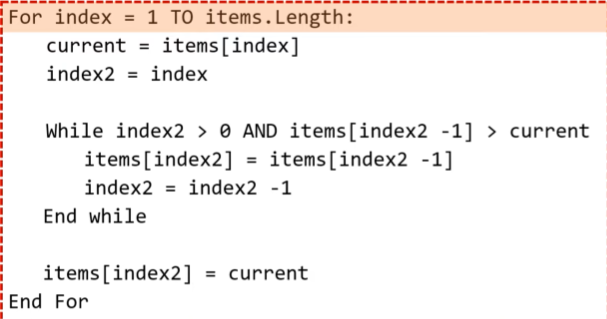
how does an insertion sort work

• mark the first element in the array as sorted

• compare the first element in the unsored part of the array with items before it

• shift elements to the right until you find the correct spot

• insert the element into the sorted list

• repeat for all remaining elements

insertion sort complexities

• time = O(n²)

• space = O(1)

• useful for small data sets

• inefficient for large data sets

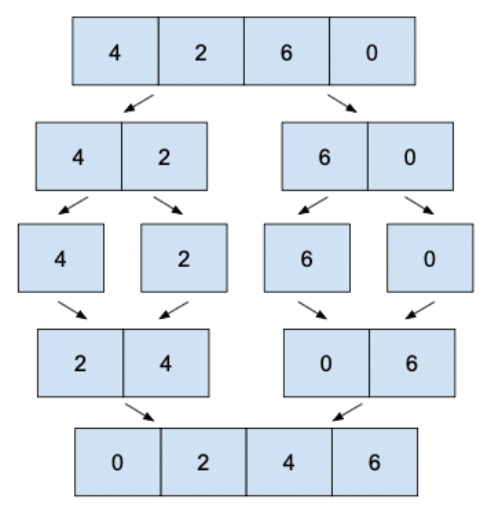
how does a merge sort work

• divide and conquer

• deconstruction and reconstruction

• continuously split the array in half (recursion) until each sub-lists contains only 1 item

• compare the individual items

• merge them into temporary arrays with the smallest item going at the start

• continuously merge the smaller arrays into a larger one, inserting items in the correct order

merge sort complexities

• time = O(nlogn) takes same amount of time even if elements are ordered

• space = O(n)

• suitable for all data sets but works better for large data sets where memory is not a concern

• idea for parallel processing environments where the concept of divide and conquer can be used

• hard to code

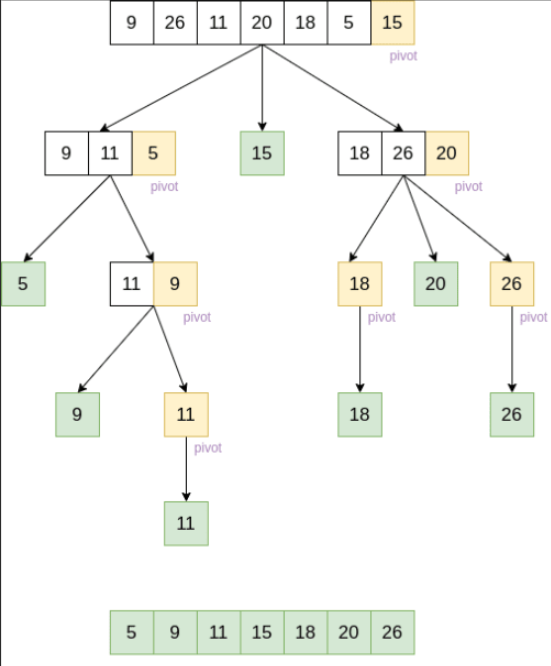
how does a quick sort work

• pick a pivot element from the list

• the pivot will be used to split the list

• go through the list and put

  • smaller values on the left

  • larger values on the right

• repeat quick sort on the left and right sub-lists

• the right element becomes the pivot for that sub-list

• the final sorted list is the sorted left + pivot + sorted right

quick sort complexities

• time, worst case = O(n²)

• space = O(1)

• fast as it uses divide and conquer

• more efficient than merge sort as it uses less memory

• suitable for any data set but better with larger ones

• ideal for parallel processing environments where the concept of divide and conquer can be used

bubble sort in pseudocode

bubble sort in python

insertion sort in pseudocode

insertion sort in python

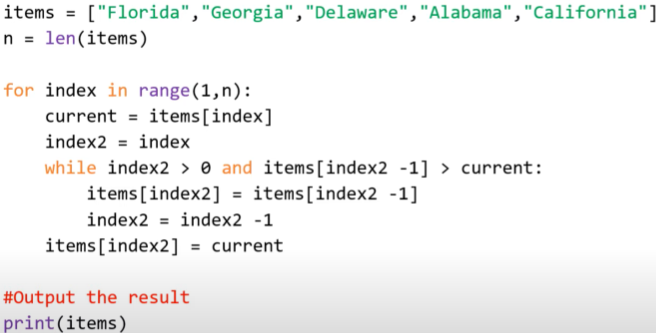
merge sort stages when programming

quick sort stages when programming