math 2

A table of values for a function f is given below. Estimate the slope of the tangent line to the curve y = f (x) at x = 1. x 0.9 0.99 1.0 1.01 1.1 f (x) 2.45 2.9405 3.0 3.0605 3.65

6 (use values around 1, don’t actually subtract 1)

if a stone is dropped from a height of 450 meters, its position at time t seconds is given by

s(t) = 450 − 4.9t2.

a. Find the average velocity over the time interval [4, 5].

a. Average velocity on [4,5]: −44.1 m/s.

if a stone is dropped from a height of 450 meters, its position at time t seconds is given by

s(t) = 450 − 4.9t2.

b. Estimate the instantaneous velocity at t = 4 seconds.

-39.2 m/s

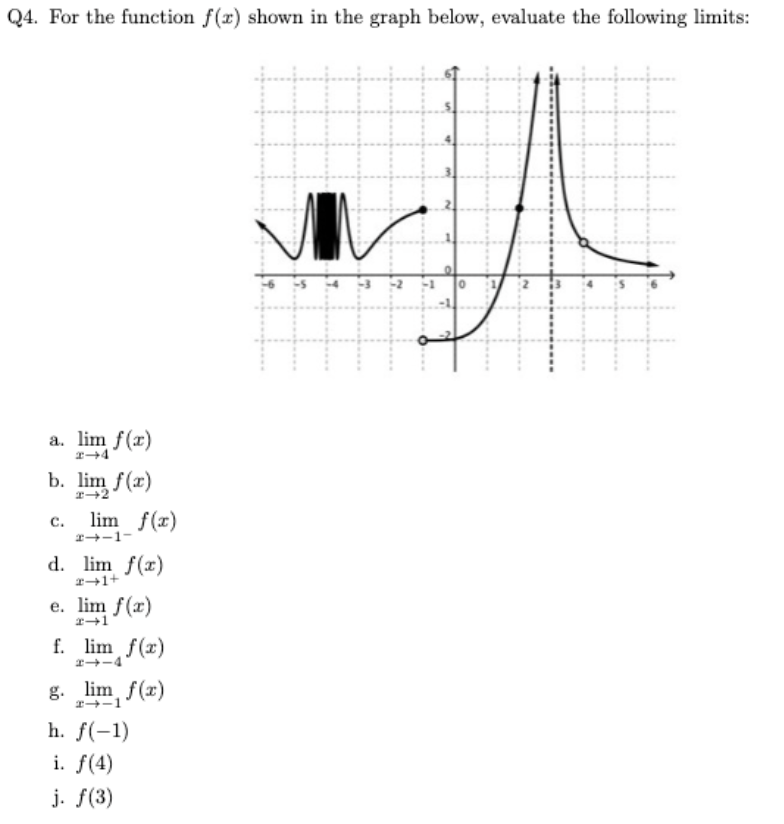
lim

x→4 f (x)

b. lim

x→2 f (x)

c. lim

x→−1−

f (x)

d. lim

x→1+ f (x)

e. lim

x→1 f (x)

f. lim

x→−4 f (x)

g. lim

x→−1 f (x)

h. f (−1)

i. f (4)

j. f (3)

a. lim⁡x→4f(x)=1
b. lim⁡x→2f(x)=2.
c. lim⁡x→−1−f(x)=2.
d. lim⁡x→1+f(x)=0.
e. lim⁡x→1f(x)=0.
f. lim⁡x→−4f(x)does not exist (the function oscillates wildly near x=−4
g. lim⁡x→−1f(x)=2.

h. f(−1)=2
i. f(4) does not exist (there is an open circle at (4,1)
j. f(3) does not exist (no value is defined at x=3

Q8. Evaluate the following limits using direct substitution, if possible:

c. lim

x→π(sin x + cos x)

-1

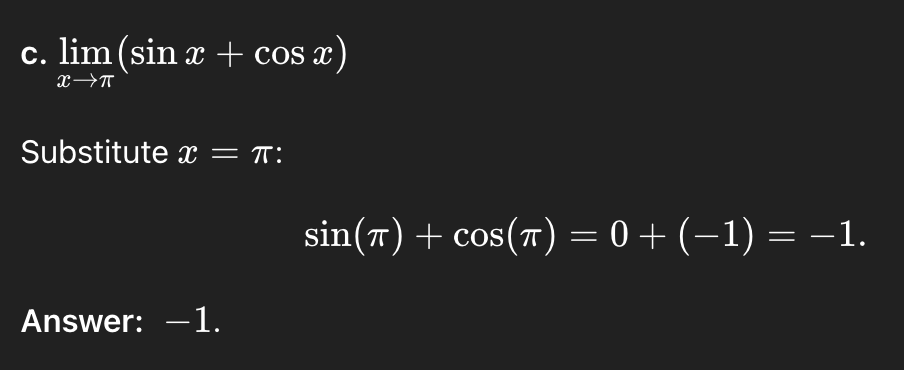
valuate the following limits by factoring or simplifying algebraically:

c. lim

h→0 (4 + h)2 − 16/h

8

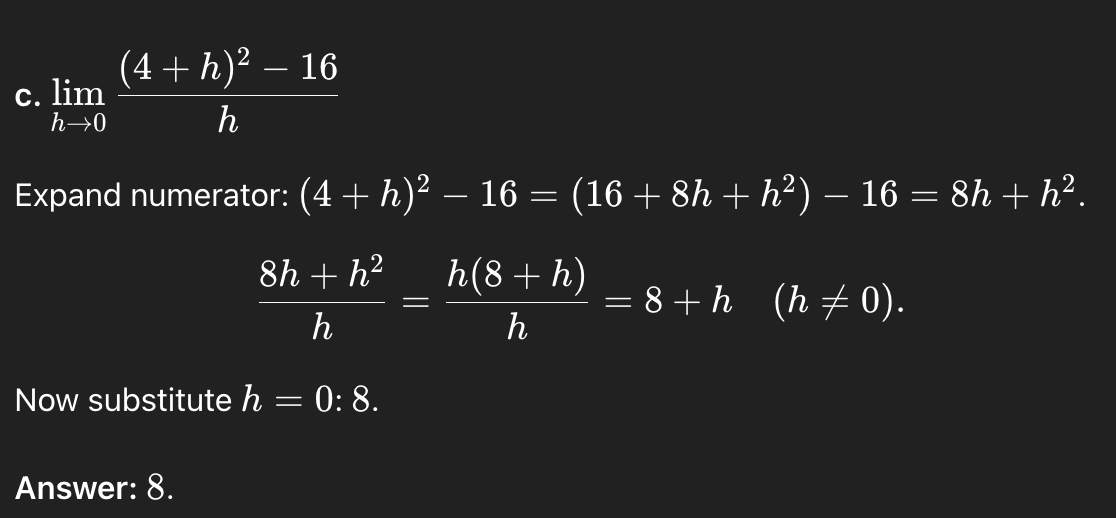
lim​x→1 x³-1/x²-1

3/2 difference of cubes

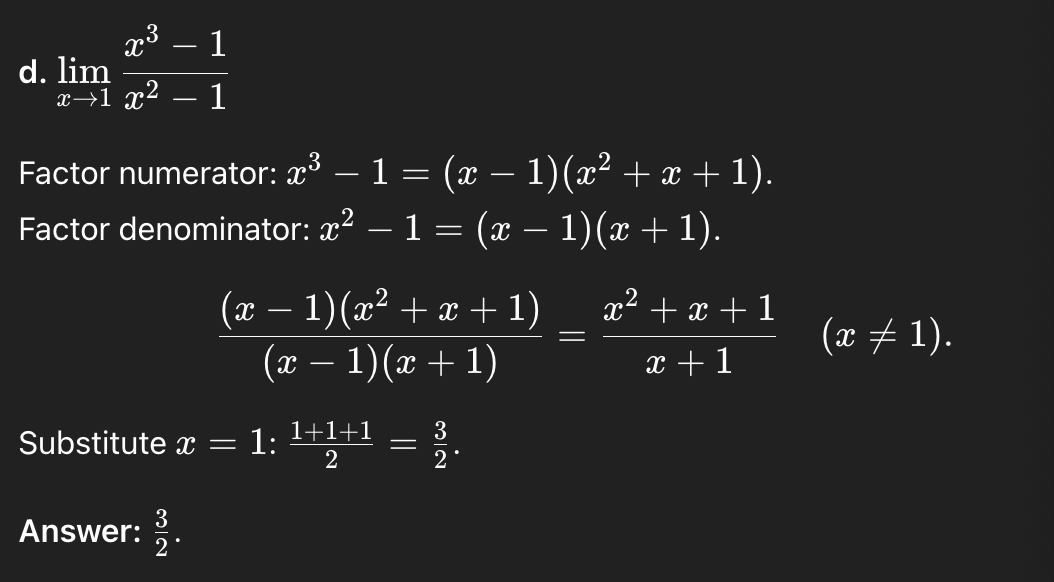
lim​t→0 t³-4t²/t²-2t

0

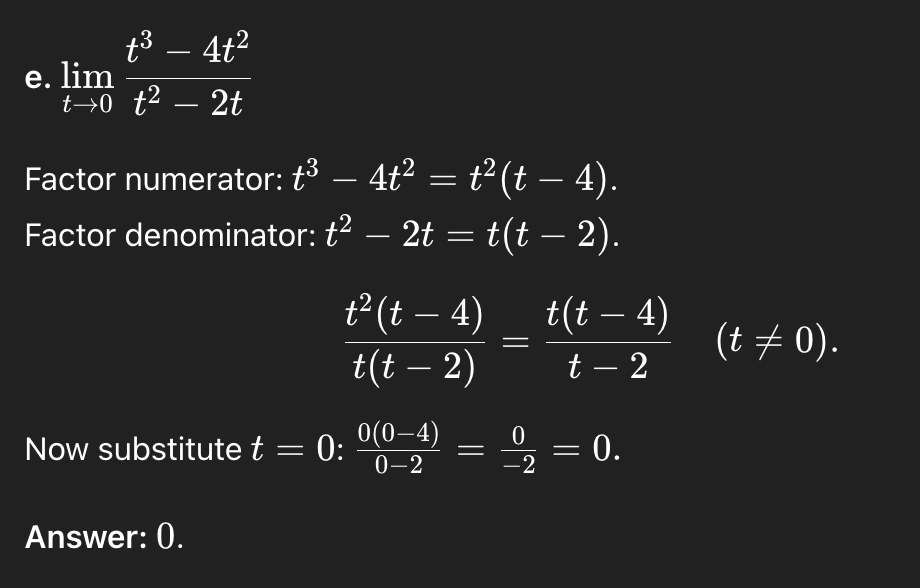
y³+8/y+2 y→-2

12 difference of cubes

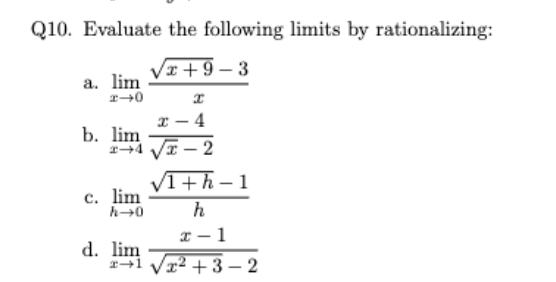
lim

x→0

√x + 9 − 3/

x

1/6 (conjugate)

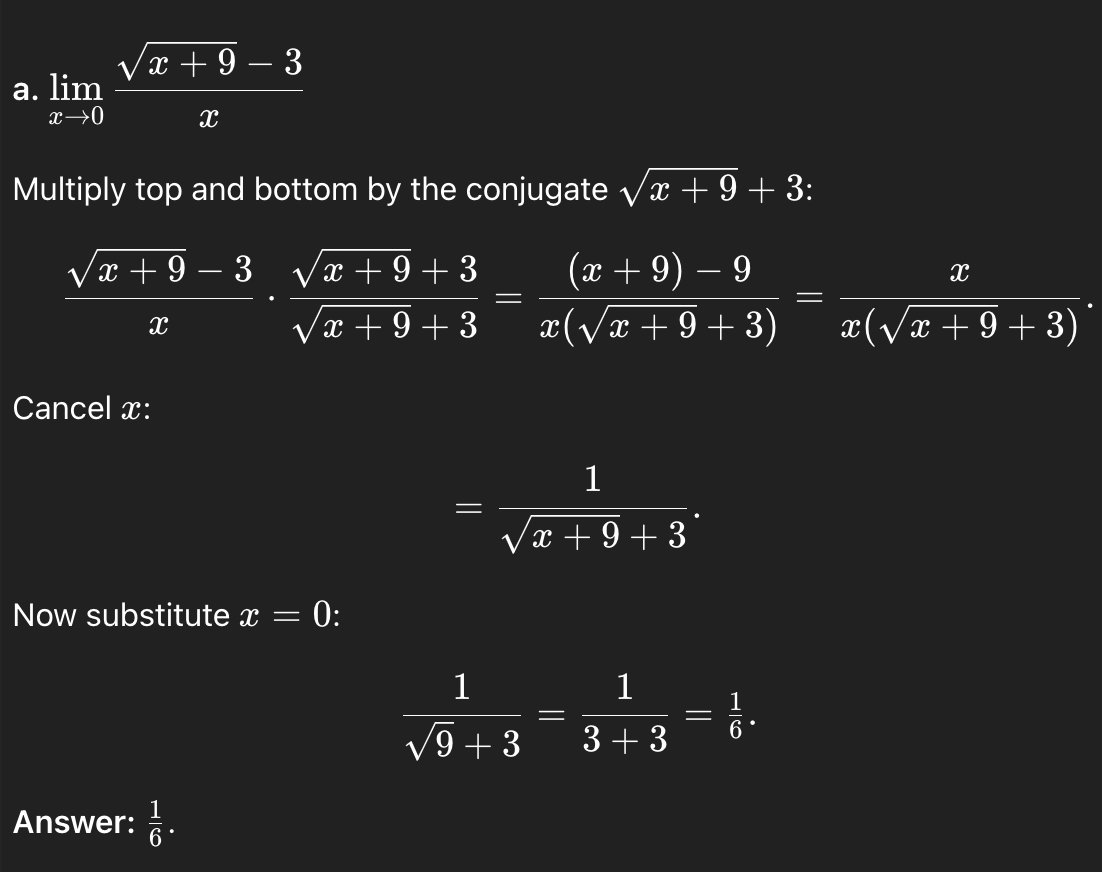
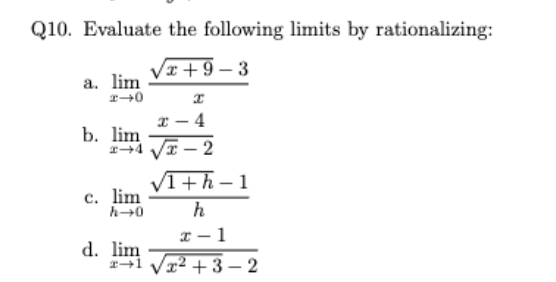
lim

x→4

x − 4/

√x − 2

4 (factor)

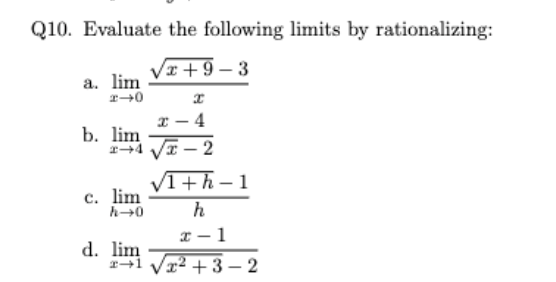
lim x→1

x − 1/

√x2 + 3 − 2

2 (conjugate)

a

5

c

6

ab

+infinity. -infinity

cd

+infinity, -infinity

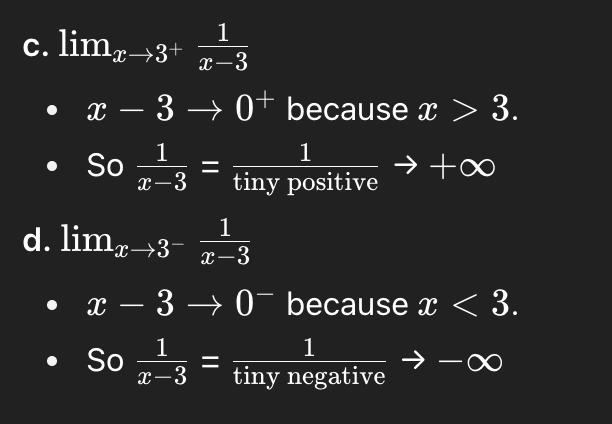
ef

+infinity, +infinity

15

continuous everywehere

16

not continuous but can be by f(1)=2

17

1/3

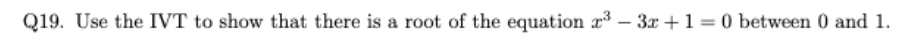
use the IVT to show that there is a root of the equation x3 − 3x + 1 = 0 between 0 and 1.

there is at least one root in the interval (0,1).

bc

∞, 0

ef

−∞, 1

gh

-1,0

21

2,-2,2

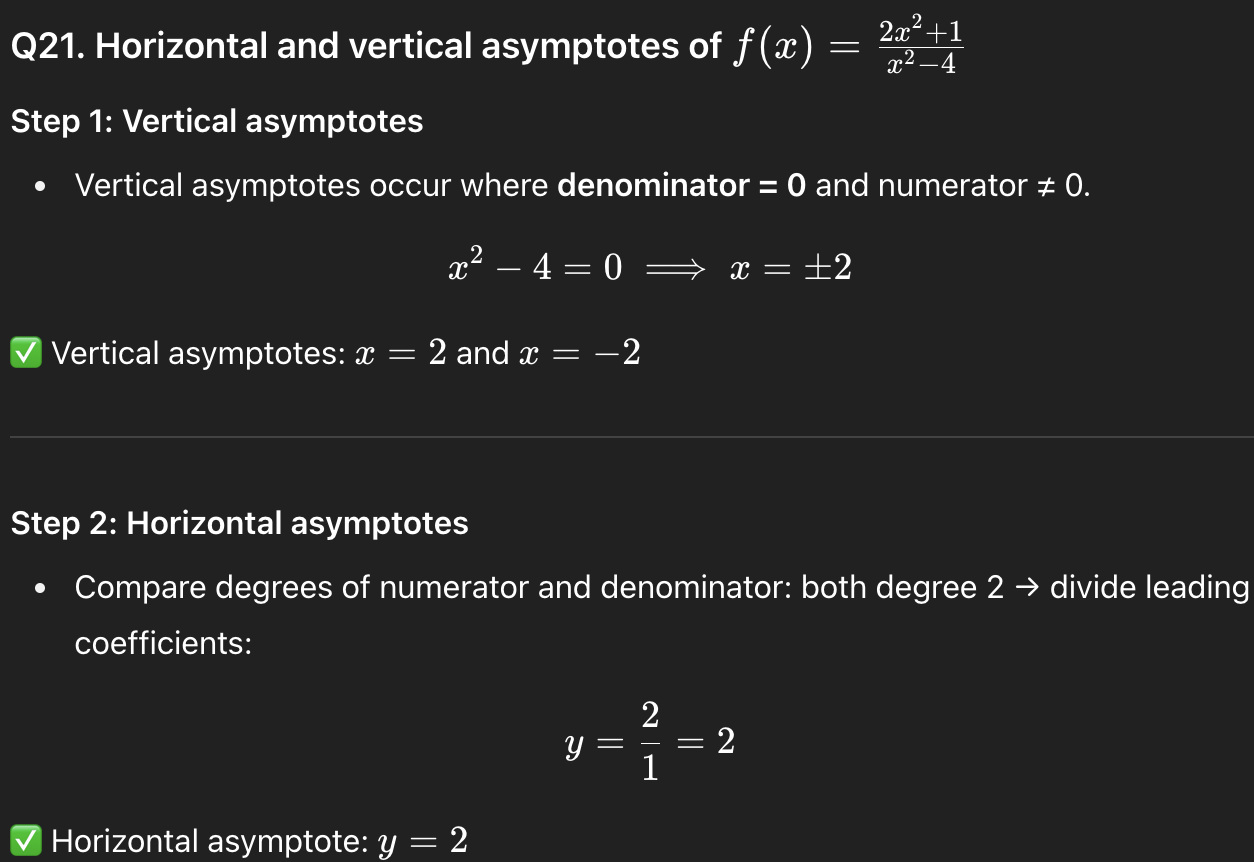
24

-1/a²

25

4x-1

26

28

31

32

33

34

35

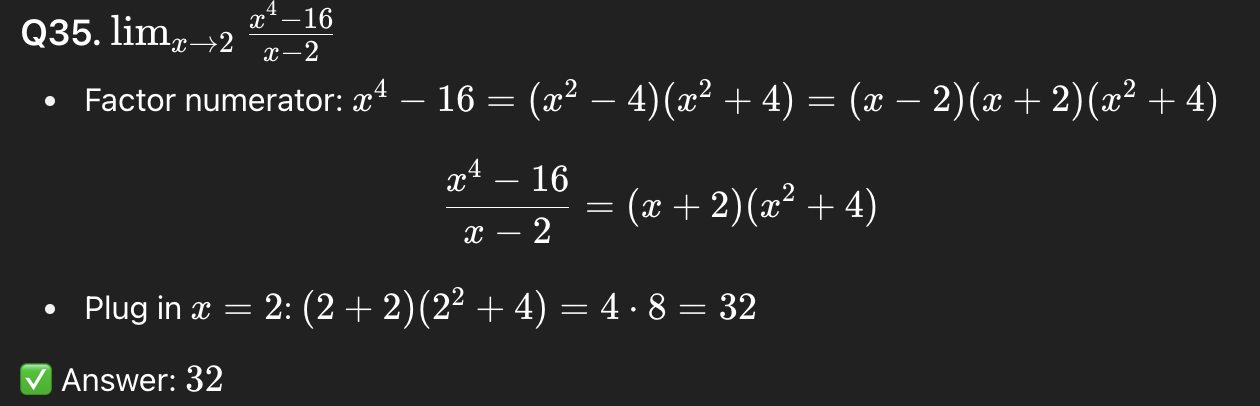
37

38

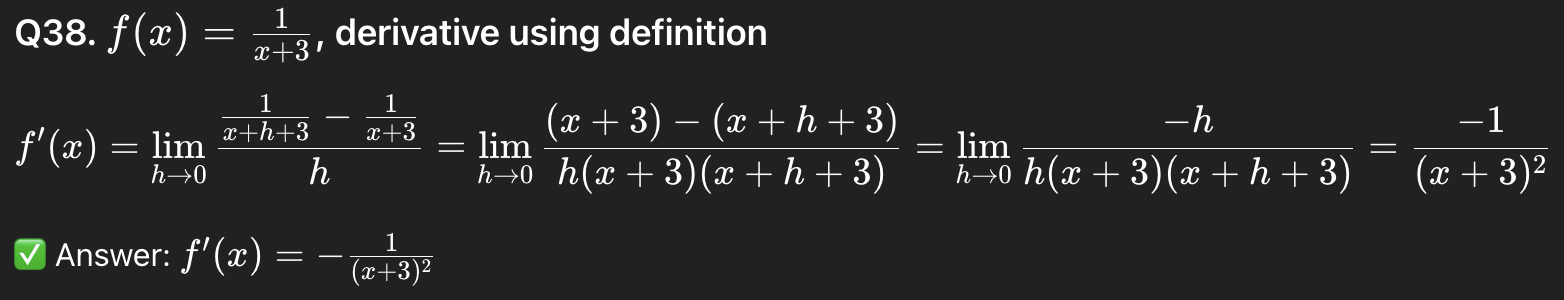
43

44

46

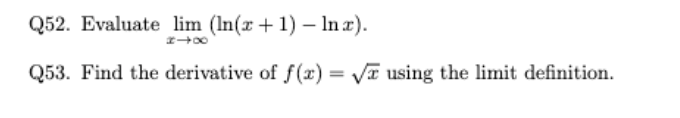
52

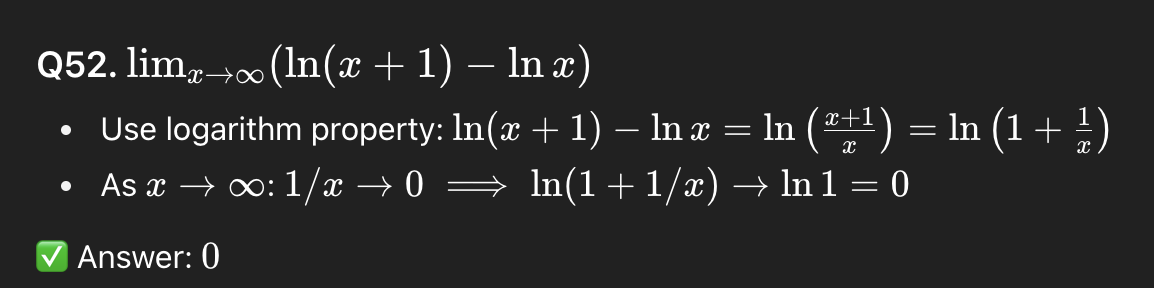
53

54

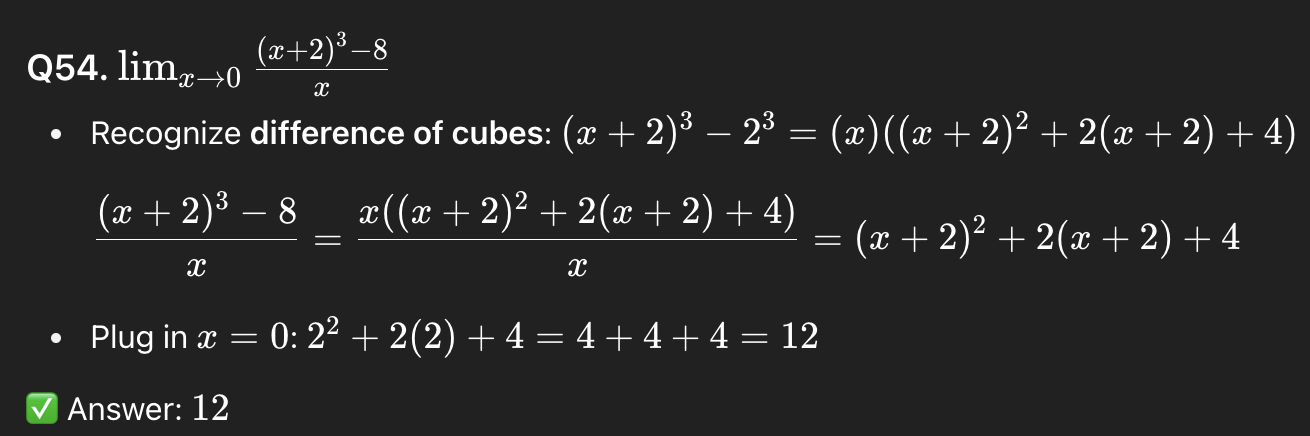
57

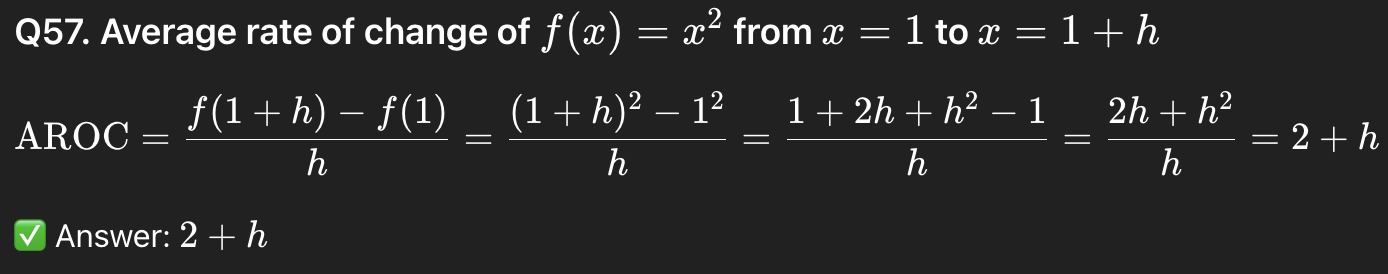
58

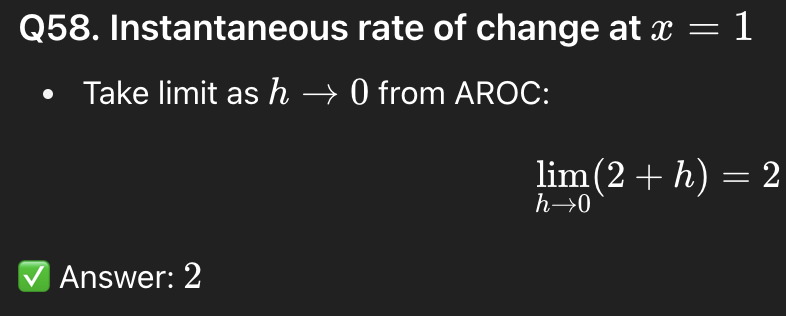
61