Improper Integrals
1/15
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
16 Terms
Improper Integrals
Definite integrals that do not satisfy the Fundamental Theorem of Calculus, where:
If f is a continuous function on [a, b], and F is any antiderivative of
f on [a, b], then the b∫a f(x)dx = F(b) - F(a)
Types of Improper Integrals
One or both limits of ∫ are infinite.
There’s and infinite discontinuity (vertical asymptote) either at one of the endpoints of [a,b] or at a point WITHIN the interval
Convergence:
If an improper integral evaluates to a FINITE numerical value, then it converges
Divergence
The improper integral doesn’t evaluate to a finite number, ie ∞
the p-integral over [a, ∞)
For a > 0:
the integral converges if p > 1
the integral diverges if p <= 1
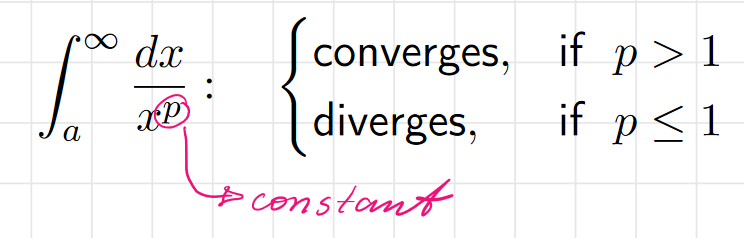
the p-integral over [0, a]
For a > 0:
the integral converges if p < 1
the integral diverges if p >= 1
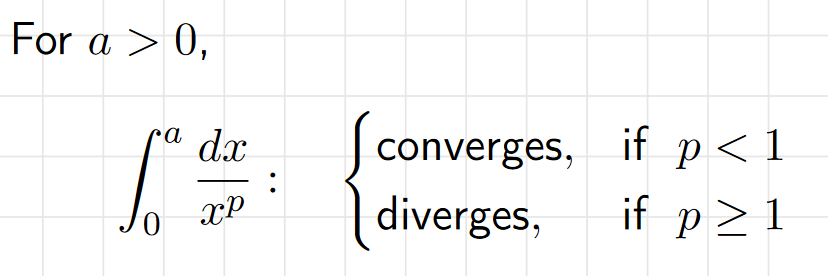
![<p>EX: Start…</p><p>This integral IS improper, when it isn’t obvious check if there’s an infinite discontinuity (vertical asymptote) either at one of the endpoints of [a,b] or at a point WITHIN the interval</p>](https://knowt-user-attachments.s3.amazonaws.com/0dd6eb30-b7c8-4308-bd28-63241ac644cd.jpeg)
EX: Start…
This integral IS improper, when it isn’t obvious check if there’s an infinite discontinuity (vertical asymptote) either at one of the endpoints of [a,b] or at a point WITHIN the interval
Split the integral in two.
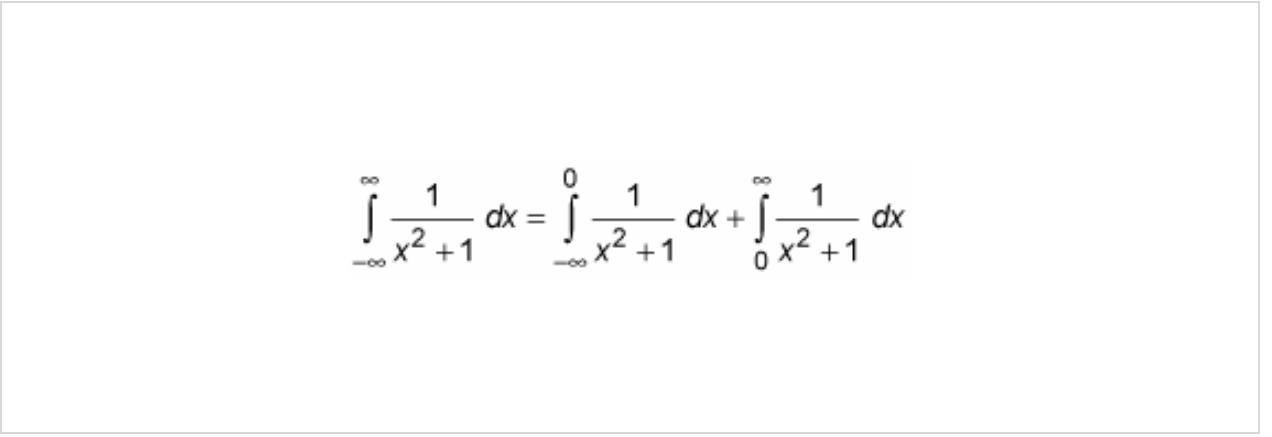
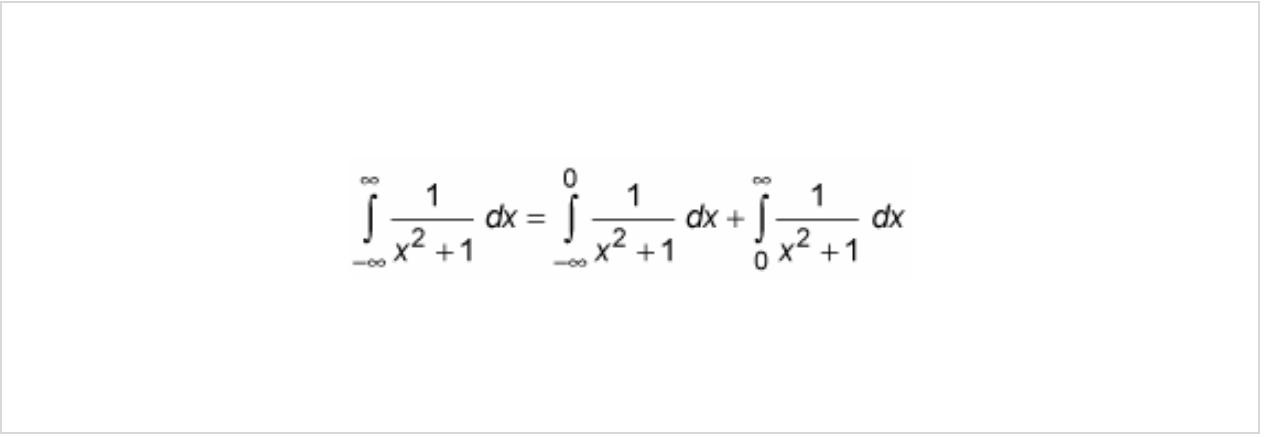
EX: After splitting the integral…
Turn each part into a limit.
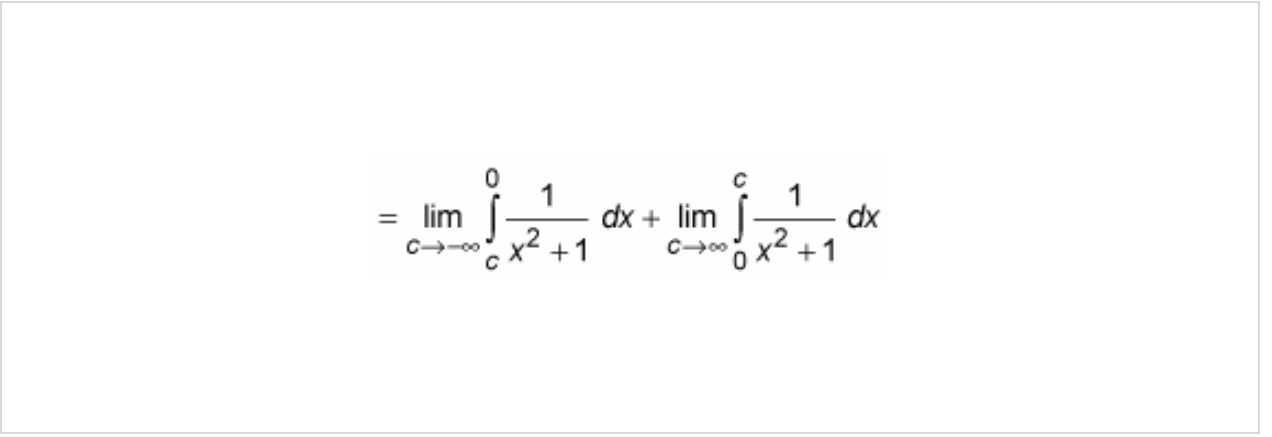
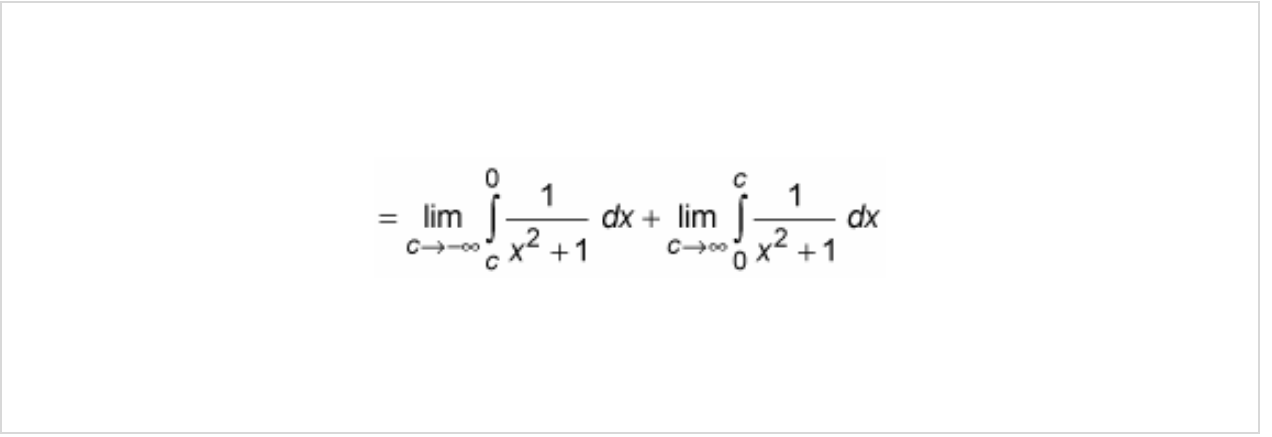
EX: After turning each part into a limit…
Evaluate each part and add up the results.

WARNING!!!!!
If either “half” integral diverges, the whole diverges. You can’t, for example, get infinity for one integral and negative infinity for the other, and then add them up to get zero.
Evaluating Limits where C is Constant:
(C / 0) →
(C / 0) → ∞
Evaluating Limits where C is Constant:
(C / ∞) →
(C / ∞) → 0
Evaluating Limits where C is Constant:
(∞ / C) →
(∞ / C) → ∞
Evaluating Limits where C is Constant:
(0 / ∞) →
(0 / ∞) → 0
Evaluating Limits where C is Constant:
(∞ / 0) →
(∞ / 0) → ∞
Evaluating Limits where C is Constant:
(0 / C) →
(0 / C) → 0