Pure - YEAR1

Index laws:

• -

• -

• -

• -

• a^m x aⁿ = a^m+n

• a^m / aⁿ = a^m-n

• (a^m)ⁿ = a^mn

• (ab)ⁿ = aⁿ bⁿ

x²+y²=…

(x + y)(x - y)

Index laws with rational power:

• -

• -

• -

• -

• a⁰ = 1

• a^-m = 1/a^m

• a^n/m = m√aⁿ

• a^1/m = m√a

rules to manipulate surds:

• -

• -

• √ab = √a x √b

• √a/b = √a/√b

rules to rationalise denominators:

• -

• -

• 1/√a x √a/√a

• 1/a + √b x a - √b/a - √b

what is a domain

the set of possible inputs for a function

what is a range

the set of possible outputs of a function

the discriminant rules:

• -

• -

• -

• b² - 4ac > 0, f(x) has two distinct real roots

• b² - 4ac = 0, f(x) has one repeated root

• b² - 4ac < 0, f(x) has no real roots

translate y = f(x) + a

(0)

(a)

translate y = f(x + a)

(-a)

(0)

translate y = af(x)

stretched by a scale factor of a in the vertical direction

translate y = f(ax)

stretched by a scale factor of 1/a in the horizontal direction

translate y = -f(x)

reflection of the graph in the x-axis

translate y = f(-x)

reflection of the graph in the y-axis

equation of a line with the gradient m that passes through the point with coordinates (x1, y1):

y - y1 = m(x - x1)

distance between two coordinates:

(x1, y1), (x2, y2)

√(x2 - x1)² + (y2 - y1)²

equation of a circle with centre (0, 0)

x² + y² = r²

equation of a circle with centre (a, b)

(x - a)² + (y - b)² = r²

Coefficients in the expansion of (a + b)ⁿ

found in the (n + 1)th row of Pascal’s triangle

ⁿC_r

n!/r! x (n-r)!

Binomial expansion

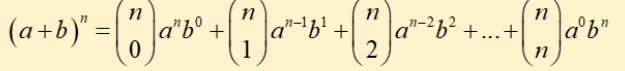
cosine rule

a² = b² + c² - 2bc cos A

sine rule to find the length of a missing side

a/sin A = b/sin B = c/sin C

sine rule to find a missing angle

sin A/a = sin B/b = sin C/c

area of triangles when you know two sides and the angle

½ ab sin C

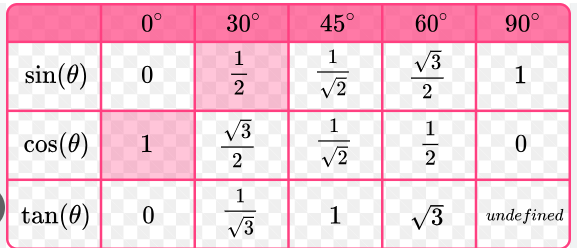
exact values of trigonometric ratios

f’(x) = …

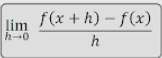
differentiating rules:

• -

• f(x) = xⁿ, f’(x) = nx^n-1

The function f(x) is increasing on the interval [a, b] if…

…f’(x) >= 0 for all values of x such that a < x < b

The function f(x) is decreasing on the interval [a, b] if…

…f’(x) <= 0 for all values of x such that a < x < b

If a function f(x) has a stationary point when x = a then when is the point a local minimum

if f’’(a) > 0

If a function f(x) has a stationary point when x = a then when is the point a local maximum

if f’’(a) < 0

If a function f(x) has a stationary point when x = a then when is the point a local maximum, local minimum or a point of reflection

if f’’(a) = 0

Integrating rule

xⁿ = x^{n + 1}/n+1 + c

laws of logarithms

• -

• -

• -

• log_ax + log_ay = log_axy (multiplication law)

• log_ax - log_ay = log_ax/y (division law)

• log_a(x^k) = k log_ax (power law)

logarithms in special cases

• -

• -

• -

• log_a1 = 0

• log_aa = 1

• log_a1/x = log_ax^-1= -log_ax

when e^x=5

ln(e^x) = ln5

x = ln5