Appendix F :(F.1 Interest and Future Values, F.2 Present Values) Exam Flashcards

Interest

Payment for use of another party’s property

Three elements That Dictate the Amount of Interest

1. principal (p) = The original amount borrowed or invested

2. Interest Rate (i) = An annual percentage of the principal

3. Time (n) = the number of periods over which the principal is borrowed or invested

Simple Interest

Computed on the the principal amount only; the return on the principal only (use the annual interest rate unless stated otherwise)

Simple Interest Forumla

Interest = (p) x (i) x (n)

Compound Interest

Computed on principal and on any interest earned that has not been paid or withdrawn; the return on principal for two or more periods at a time; uses an accumulated balance at each year-end to computer interest in the succeeding year

Future Value of a Single Amount

value at a future date of a given amount invested

Future Value Formula

Annuity

A series of payments or receipts of equal dollar amounts

Future Value of Annuity

The sum of all payments (receipts) plus the accumulated compound interest on them

To compute you must know:

1. The Interest Rate

2. The Payments (Receipts)

3. The Amount of Periodic Payments (Receipts)

Future Value of Annuity Formula

The future value of an annuity formula calculates the value of a series of equal payments at a future date, taking into account interest earned.

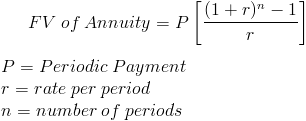
Present Value

The value now of a given amount to be paid or received in the future, assuming compound interest

Present Value Formula

FV = Future Value

PV = Present Value

r = Interest Rate

n = Time (number of periods)

The Present Value of Annuity

The value now of of a series of future receipts, payments, discounted assuming compound interest

To compute you must know:

1. the discount rate

2. the number of payments (receipts)

3. the amount of periodic payments (receipts)

The Present Value of Annuity Formula

Time Period & Discounting

Sometimes discounting doesn’t happen on an annual basis (monthly, quarterly, semiannually) as a result, we must adjust the annual interest rate for this:

Assume, for example, that an investor received $500 semiannually for three years instead of $1,000 annually.

In this case, the number of periods becomes six (3 × 2), the discount rate is 5% (10% ÷ 2), the present value factor is 5.07569 (6 periods at 5%), and the present value of the future cash flows is $2,537.85 (5.07569 × $500).

Present Value of a Long Term Note or Bond

The PV (or market price) of a long term note or bond is a function of these three variables:

1. The payment amounts

2. The length of time until the amounts are paid

3. The discount rate

The first variable (dollars to be paid) is made up of two elements:

1. A series of interest payments (an annuity)

2. The principal amount (a single amount)

To compute the the PV of the bond, both the interest payment and the principal amount must be discounted - two different computations