Unit 5 and 6 Geometry 25-26 IHS Sem 1 Online

equilateral triangle

three congruent sides

iscoleces triangle

two congruent sides

-vertex: b/w 2 congruent sides

-leg: two congruent sides

-vertex angle: angle between legs

-base: opposite of vertex, non congruent side

-base angle: angles opposite of the legs, always congruent to each other. sides of base angles are also congruent

-can use TST and isosceles triangle theorem to find missing angles and sides

converse of iscosceles triangle theorem

If the base angles of a triangle are congruent, then the sides opposite those angles are congruent

scalene triangle

triangle with no congruent side lengths

acute triangle

all 3 angles are acute

obtuse triangle

one obtuse angle

right triangle

one right angle

hypotenuse

opposite of right angle

equiangular

all right angles are congruent

-has to be acute and equilateral

-have to be 60 degrees

Triangle Sum Theorem

3 angles add up to 180

Pythagorean Theorem

a²+b²=c²

-for right triangles only

-hypotenuse: longest side of right triangle

-3-4-5 triangle

-used to find missing sides

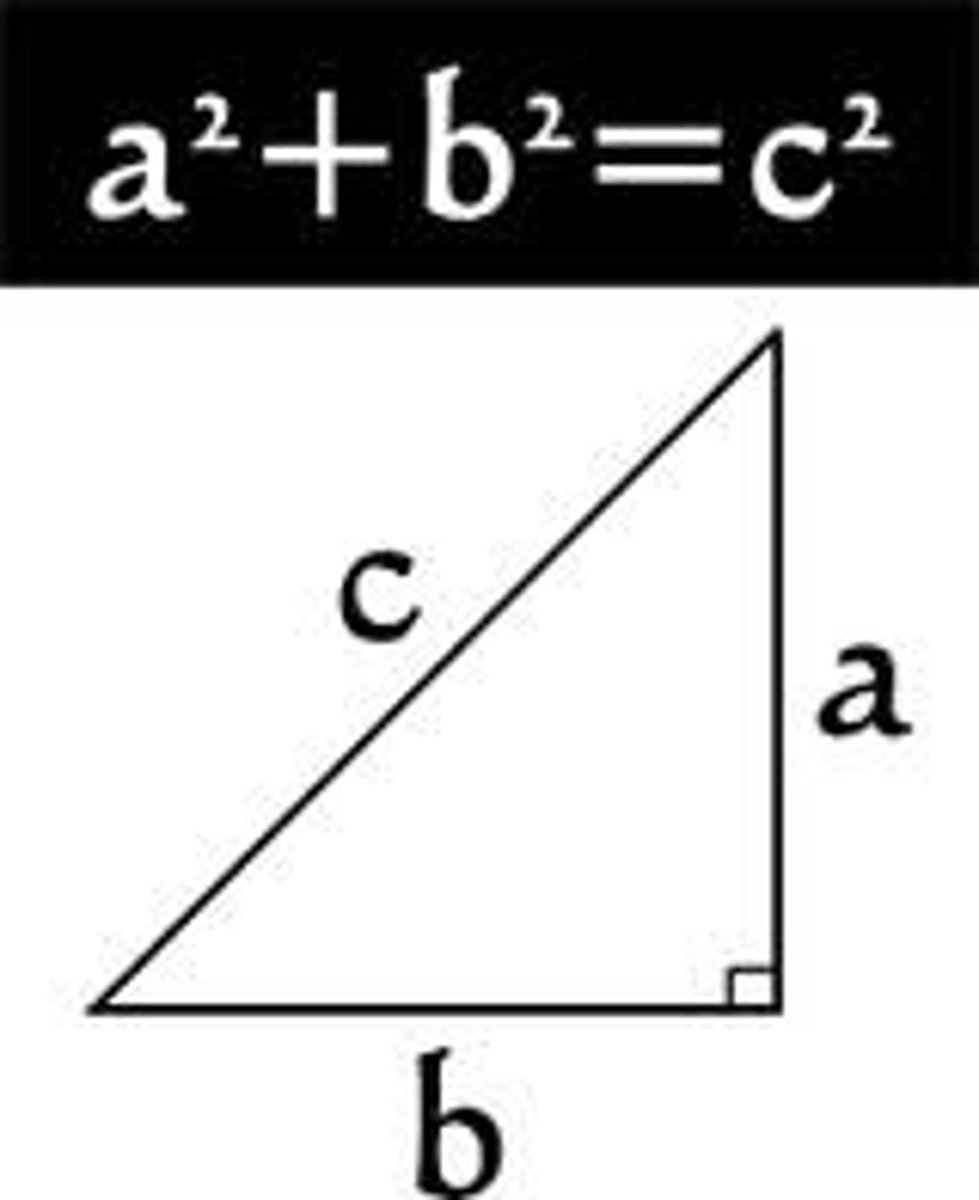
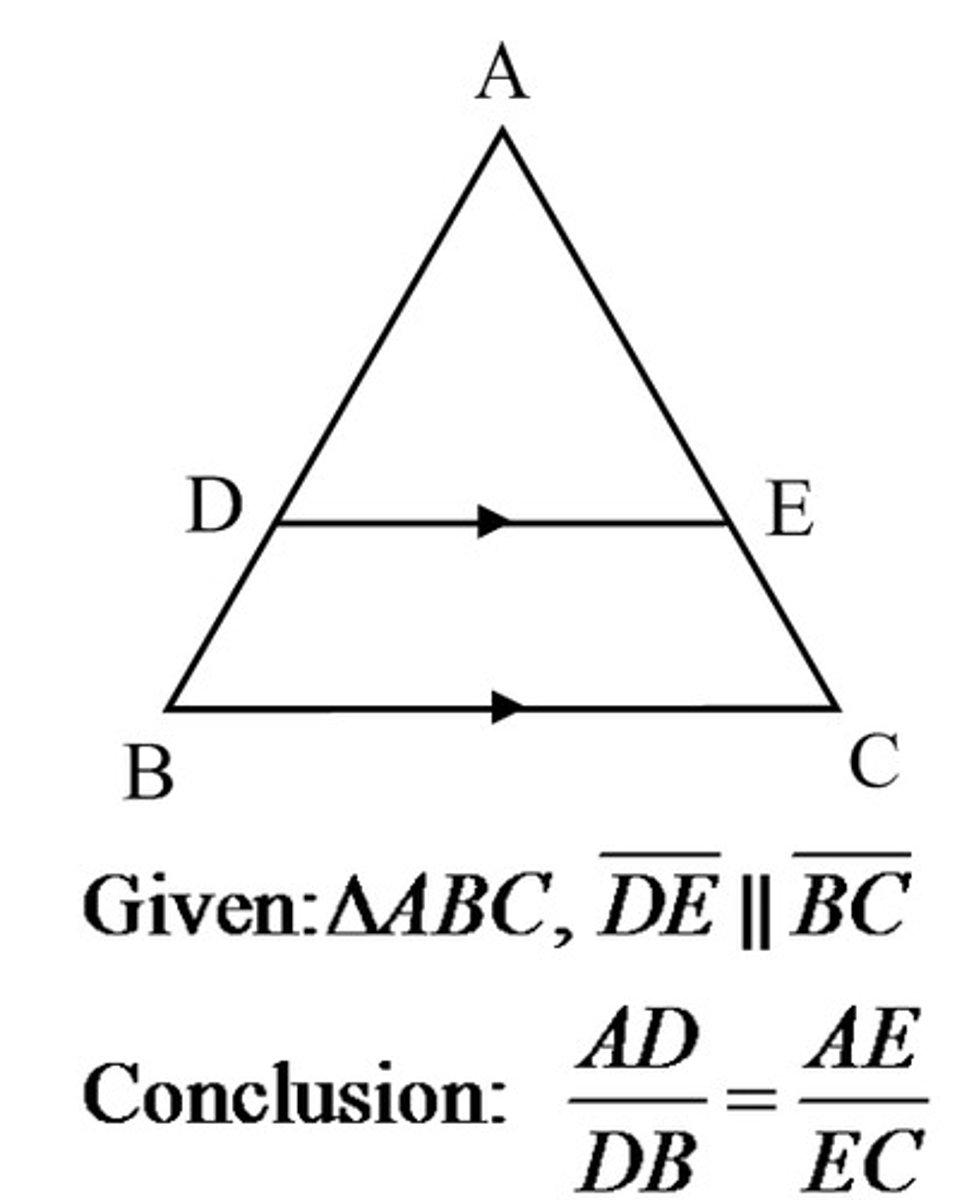
triangle proportionality theorem

If a line parallel to one side of a triangle intersects the other two sides, then it divides the two sides proportionally

-Set up the proportion. a/b=c/d Then solve the proportion using the cross product method.

median

connects vertex to midpoint

-Each triangle has 3 medians that will intersect in the middle, creating a centroid

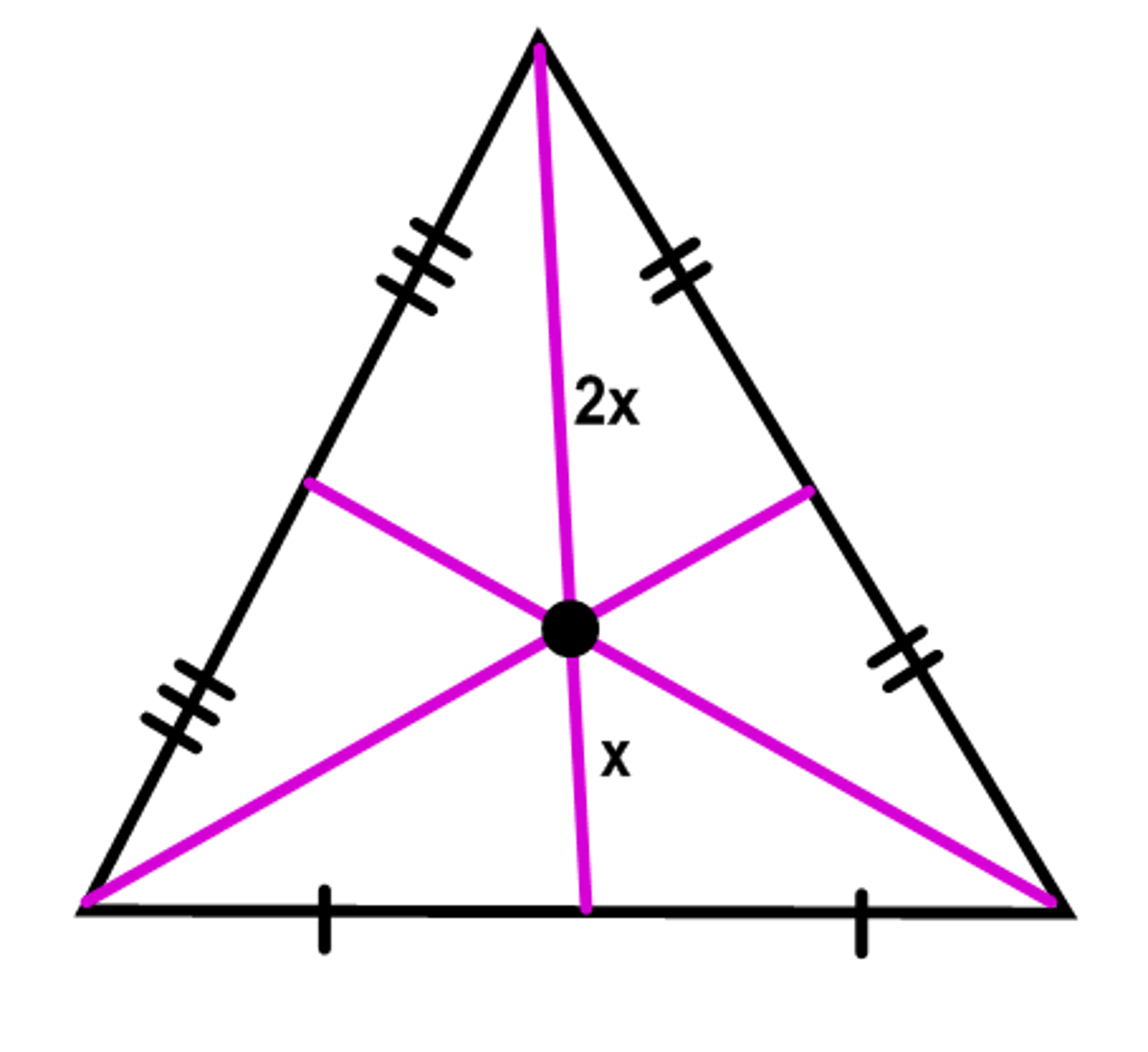
Centroid

exactly 2/3 of the distance from each vertex to midpoint of the opposite side, center of triangle

midpoint formula

(x₁+x₂)/2, (y₁+y₂)/2

altitude

height of object

-runs perpendicular to opposite side

-triangles have 3 altitudes

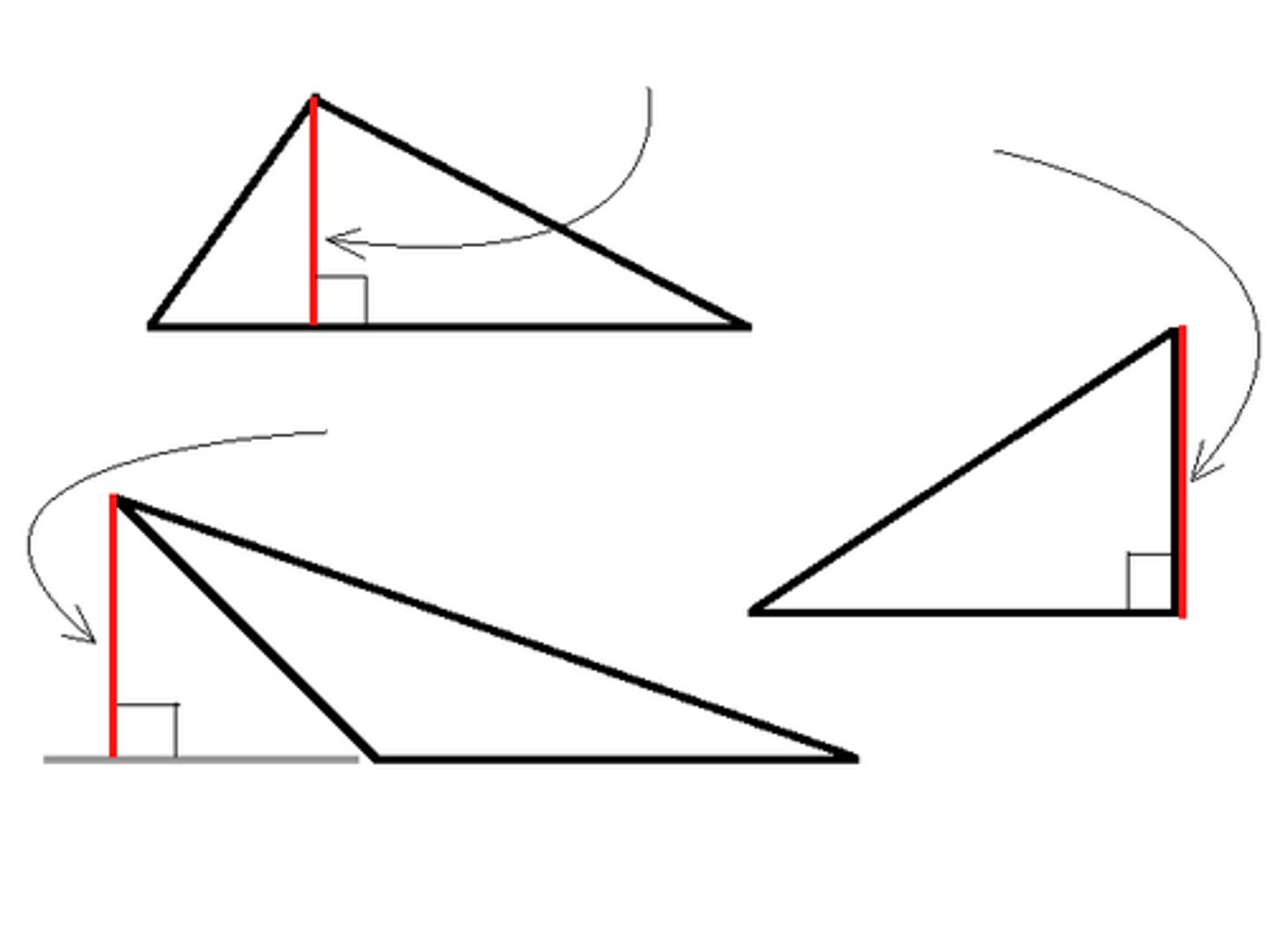
orthocenter

point of concurrency of the altitudes

-off center

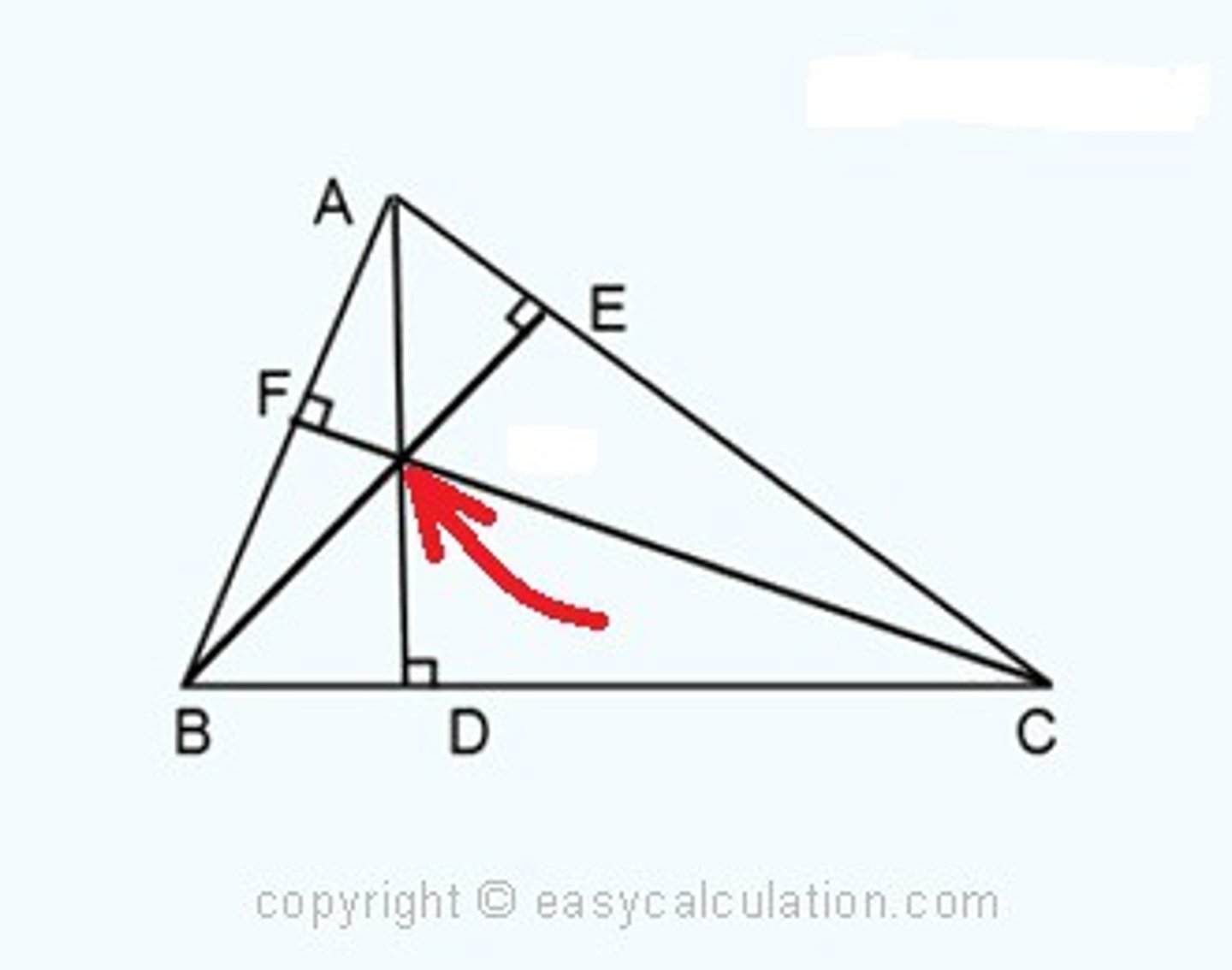
concurrent

intersect at one point

fulcrum

anchor point that connects two sets of legs

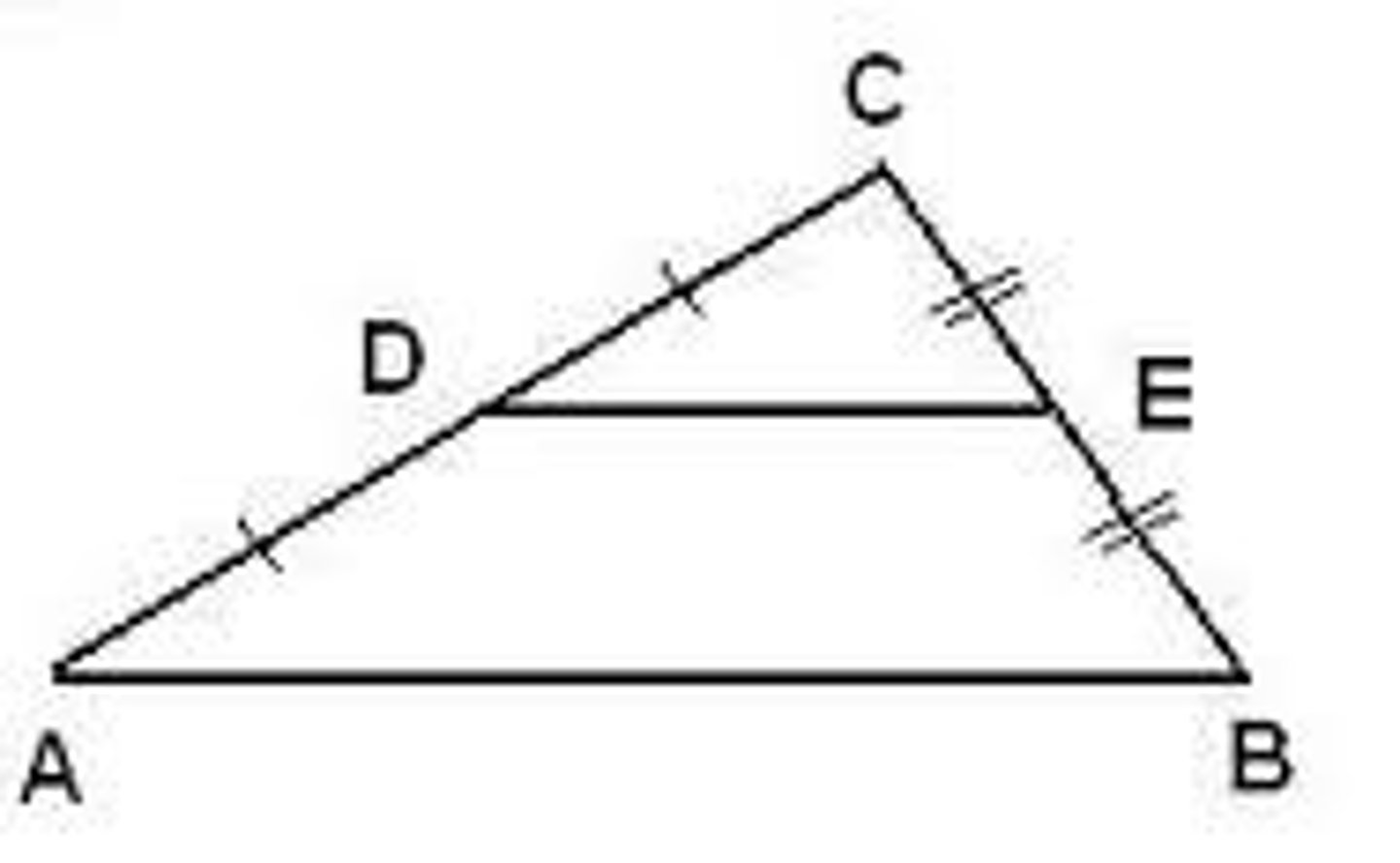
midsegment

finite line with two end points

-two endpoints are midpoints

-every triangle has 3 midsegments

distance formula

d = √[( x₂ - x₁)² + (y₂ - y₁)²]

Midsegment Theorem

segment connecting the midpoints of two sides of a triangle is parallel to the third side and half as long

-same slope

-1/2 as long

slope

amount of incline/slant in an object

-pos, neg, or 0

-y2-y1 over x2-x1 if same slope = parallel

trapezoid

A quadrilateral with exactly one pair of parallel sides

-nonparallel sides: legs

-parallel sides: bases

-altitude: perpendicular distance between bases

-median: connects opposing legs, 1/2 of the sum of the bases

Midsegment Trapezoid theorem

The midsegment of a trapezoid is parallel to the bases and its length is equal to the average of the lengths of the two bases.

triangle inequality theorem

any side of a triangle must be shorter than the sum of the lengths of the other two sides

- x < 14 + 10, x must be less than 24

- 1051 < x + 979, x must be greater than ___ and less than __

triangle inequality theorem equations

AC < AB + BC

BC < AB + AC

AB < BC + AC

converse of triangle inequality theorem

In a 3 sided shape, if any side is shorter than the sum of the other two sides, then a triangle exists

triangle inequality theorem for angles

The largest angle in the triangle will be opposite the longest side, and smallest angle in a triangle will be opposite the shortest side

triangle inequality theorem for angles converse

The longest side in a triangle will be opposite the longest angle and the shortest side will be opposite the smallest angle

indirect proofs

assume opposite is true and then makes an absurd point

Hinge Theorem

If two sides of one triangle are congruent to two sides of another triangle, and the included angle of the first is larger than the included angle of the second, then the third side of the first is longer than the third side of the second.

-Also known as SAS Inequality theorem

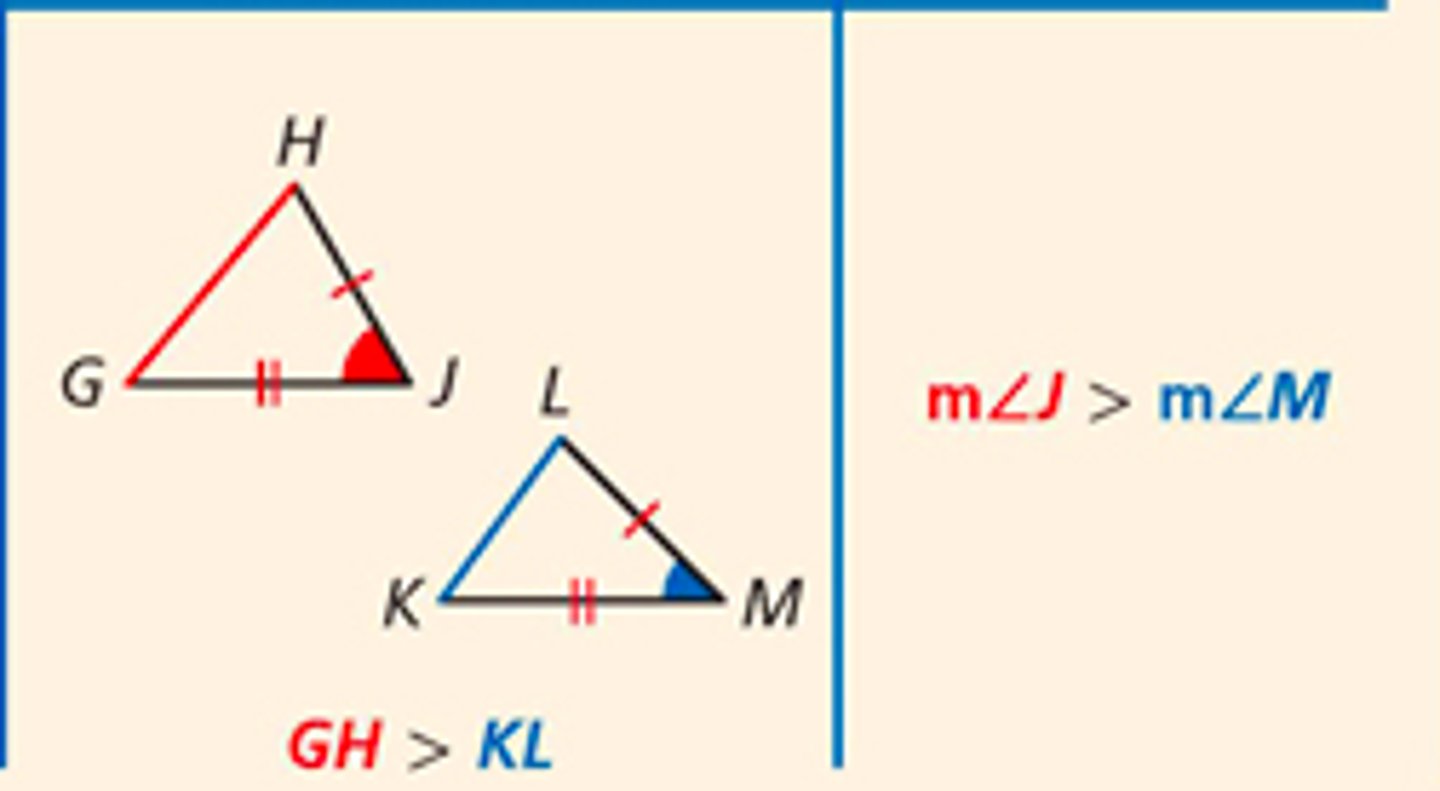
Converse of Hinge Theorem

If two sides of one triangle are congruent to two sides of another triangle, and the third side of the first is longer than the third side of the second, then the included angle of the first is larger than the included angle of the second.

-Also SSS Inequality theorem

proportional triangles

parts of similar objects are corresponding parts

<--> means corresponding

- fraction = part / whole

proportion

mathematical expression that equates two ratios

- a/b = c/d

-ad are extremes, cb are means

-can rewrite by flipping the fractions

-b/a = d/c

geometric mean

3/x = x / 12

3(12) = x^2

square root to find x which is the geo. mean

-special ratio that relates the sides of similar right triangles

altitude rule

The altitude to the hypotenuse of a right triangle is the mean proportional between the segments into which it divides the hypotenuse

-altitude: line segment that extends from 1 vertex to form a right triangle with the opposite side

-part of hypotenuse / altitude = altitude / other part of hypotenuse

Leg Rule

the length of each leg of a right triangle is the geometric mean between the length of the hypotenuse and the length of the adjacent hypotenuse segmnet

- hypotenuse / leg = leg / projection

Congruency properties

SSS, Sas, ASA, ASA, AAS, HL

triangle applications

-Hinge Theorem: use main theorem for side lengths, converse for angles

-Similarity problems will have two triangles formed. Can involve right triangles with altitude, geometric mean, leg rule, and altitude rule

-Problems may include medians and altitudes

right triangles

-one right angle and two acute

-hypotenuse is opposite right, longest side

-each acute angle has an adjacent leg and opposite leg

similar triangles

congruent corresponding angles

-proportional corresponding sides

geometric mean

nth root of the N #s

two rules for similar triangles

-Altitude from right angle of right triangle is geometric mean of two segments formed by altitude

-The length of either leg of triangle is geometric mean of the hypotenuse and segment from altitude to leg

45-45-90 triangle

hypotenuse = x√2

-x = leg

-side ratio: 1:1:square root of 2

30-60-90 triangle

-1:2:to square root of 3

-side opposite 30: x

-hypotenuse: 2x

-side opposite 60: x√3

tangent ratio

tanx = opposite/adjacent (adjacent, not hypotenuse)

-for acute angles of right triangles

-tells us X and Y coordinates of a circles radius on a Cartesian plan

-0 with a slash = theta

applying tangent ratio

use DRG mode and use "tan" on calc

SOH

opposite over hypotenuse

toa

opposite over adjacent

cah

adjacent over hypotenuse

formula to find area with sin

A = 1/2absinC

a and b are sidelengths, sin C is an angle measure

Law of Sines

sinA/a=sinB/b=sinC/c or flip it

-two triangles angles are known and 1 side

-press 2nd to get inverse of sine and cosine

-ASA, SAA use law of sines

height of triangle

h=bsinA

One triangle

Angle a is acute and a=h. If angle is acute/obtuse, a > h

two triangles

if angle A is acute and h < a < b, then two triangles are created

no triangles

if Angle A is acute and a < h, if angle A is obtuse and a < b or a = b

-if it is SSA, it will be an ambiguous case

steps for using law of sines

1, check for ambiguous case

2. draw a triangle if not given

3. write a proportion based on law of sines

4. solve equation to find unknown side or angle

-use inverse after proportion when solving for an angle

Law of cosines

a²=b²+c²-2bcCosA

c²=a²+b²-2abcosC

b²=a²+c²-2acCosB

-use when SAS and SSS

Formula for the area of an acute or obtuse angle

Make a right triangle: 1/2bh

Use the other formula 1/2absin(c)

Right triangles in rectangles

Use 2 congruent triangles to make a rectangle

Diagonal of a rectangle

d= √l^2+w^2

-can use sine, cosine, and tangent ratios

-can use leg ratios

2d distance formula

d = √[( x₂ - x₁)² + (y₂ - y₁)²]

3d distance formula

d=√(x2-x1)+(y2-y1)+(z2-z1)