MCAT Physics and Math - Mathematics

584

Scientific notation

method of writing numbers that takes advantage of powers of ten

powers of ten

any of the integer powers of the number ten

significand /coefficient / mantissa

the number multipled by the power of ten in scientific notation

must be a number with an absolute value in the range [1,10)

exponent

the number of times ten is multiplied into the significand in scientific notation

can be any whole number (positive, negative, zero)

Significant figures

indication of our certainty of a measurement and help avoid exceeding that certainty when performing calculations

leading zeroes

zeroes to the left of the first nonzero digit; insignificant

trailing zeroes

zeroes to the right of the last nonzero digit; can be significant or not, depending on precison of measurement

addition and subtraction

decimal points are maintained rather than maintaining significant figures

multiplication and division

maintain as many digits as possible throughout the calculations; then round to the least number of significant digits in any of the given values

multiplication: round one number up and one number down to compensate

divison: round both numbers in the same direction to compensate

Exponents

X⁰ = 1

X^A × X^B = X^{(A + B)}

X^A / X^B = X^{(A - B)}

(X^A)^B = X^{(A × B)}

(X / Y)^A = X^A / Y^A

X^-A = 1 / X^A
X^A/B = ^B√X^A

approximate square roots

determining which two perfect squares it falls between OR divide the number given to you by known squares

scientific notation: make exponent divisible by 2 to square

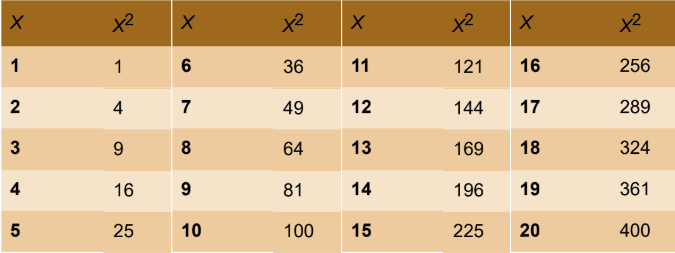
√2

approx 1.414

√3

approx 1.732

Logarithms

pX = -log X

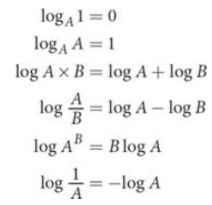
Euler’s number (e)

about 2.718

common logarithms

Base-ten logarithms (log₁₀)

natural logarithms

logarithms based on Euler’s number (log_e or ln)

convert between natural logarithms and common logarithms

log x ≈ ln x / 2.303

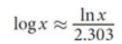
Estimating Logarithms

use scientific notation

log (n × 10m) ≈ m + n/10

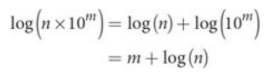
right triangle

triangle with one right 90° angle

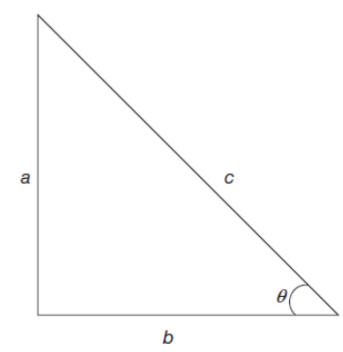
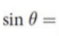
Sine

ratio between the side opposite the angle of interest and the hypotenuse

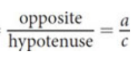
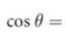
Cosine

calculated as the ratio between the side adjacent to the angle of interest and the hypotenuse

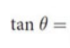
Tangent

calculated as the ratio between the side opposite the angle of interest and the side adjacent to the angle of interest

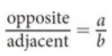
inverse trig functions

use the calculated value of sine, cosine, or tangent, and yield a numerical value for the angle of interest

sin⁻¹ or arcsin

cos⁻¹ or arccos

tan⁻¹ or arctan

Special Right Triangles

sides:

• 3-4-5

• 5-12-13

angles:

• 30−60−90

  • 1 - √3 - 2

• 45−45−90

  • 1 - 1 - √2

Common Trigonometric Ratios

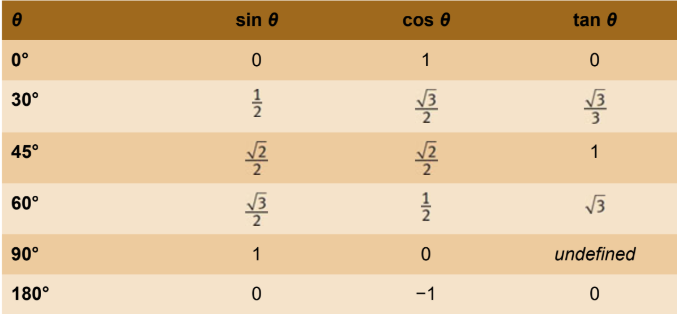
direct relationships

increasing one variable proportionately increases the other; as one decreases, the other decreases by the same proportion

inverse relationships

increase in one variable is associated with a proportional decrease in the other

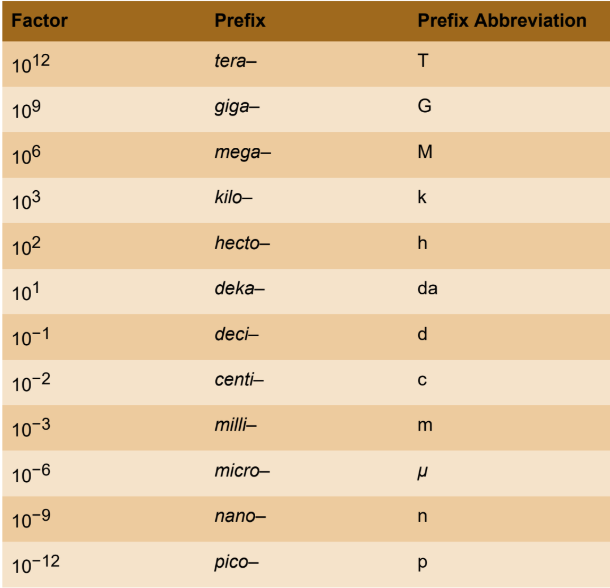
Metric Prefixes

Common Conversion Factors

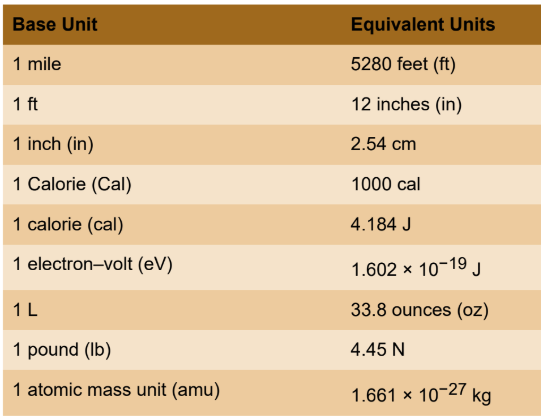
Temperature conversion

9 degrees change in F for every 5 C/K

freezing point

• in F = 32

• in C = 0

  • in K = 213.15

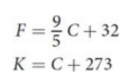
dimensional analysis

the units of the calculated answer must match the units of the answer choices and follow throughout calculations

system of equations

needs at least as many equations as there are variables

three methods:

• substituting one variable in terms of the other

• setting equations equal to each other

• manipulating the equations to eliminate one of the variables

substitution

solve for one variable in one of the equations, and then insert this term into the other equation

Setting equations equal

specialized case of substitution; solve for the same variable in both equations and then set the two equations equal to each other

elimination

multiply or divide one (or both) of the equations to get the same coefficient in front of one of the variables in both equations

then, add or subtract the equations as necessary to eliminate one of the variables