factorial designs

origins of factorial designs

Agricultural research

Looking for interactions between such factors as fertilizer type and wheat stain

Invented ANOVA

factorial design

more than one independent variable; IVs referred to as factors

notation system

Digits represent IVs

Numerical values of digits represent the # of levels of each IV

2x3 factorial (say: “two by three”)

2 IVs, one with 2 levels, one with 3 = 6 total conditions

2x4x4 factorial

3 IVs, with 2, 4, and 4 levels = 32 total conditions

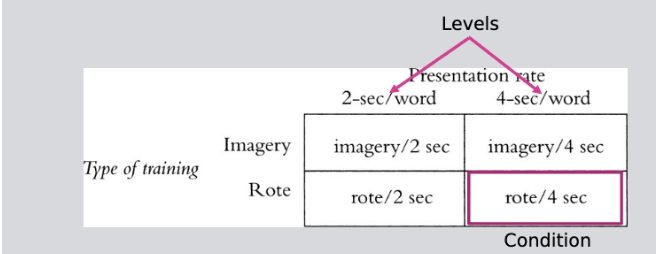
factorial matrix

2x2 (two levels each of type of training and presentation rate)
Factor 1 (two levels) and Factor 2 (two levels)
calculate row and column means

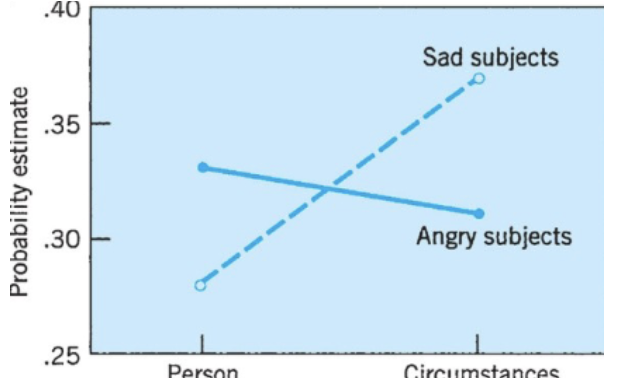
Interactions

effect of one factor depends on the levels of the other factor

Look at the means across the different combinations of factors, Compare the patterns of the means across different combinations, Statistical Analysis

main effects

refers to the impact of one factor on the dependent variable ignoring the influence of other factors

line graphs occasionally used to highlight interactions

calculate means for each level, compare means, conduct stat analysis, a sig difference means main effect exists

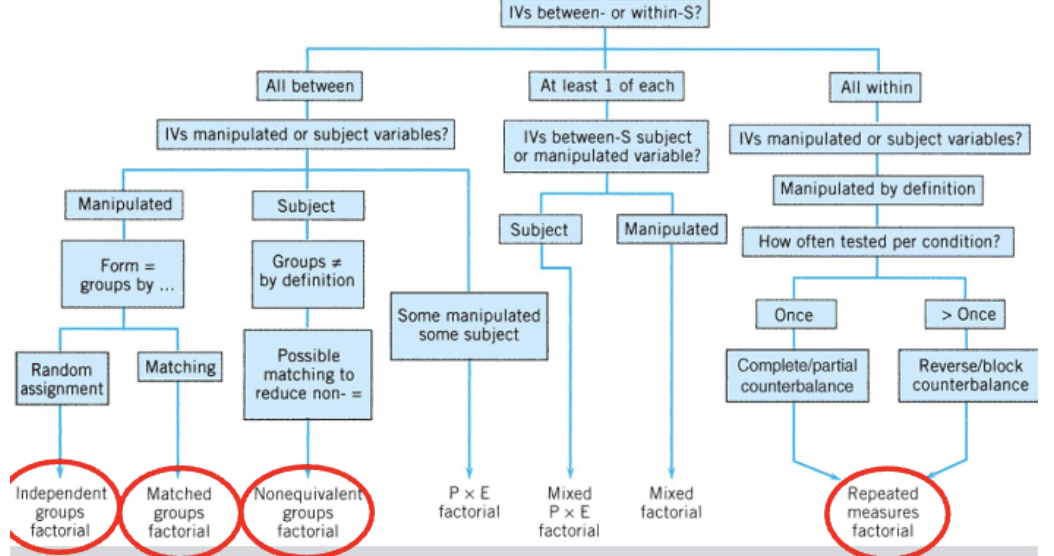
varieties of factorial designs

decision tree

mixed factorial designs

At least one IV is a between-subjects factor

At least one IV is a within-subjects design

Between-Subjects Factor: Since each participant only experiences one level of the between-subjects factor, there is no need for counterbalancing for that factor.

Within-Subjects Factor: Counterbalancing is typically used for within-subjects factors to control for order effects, but it’s not always necessary, especially if the within-subjects conditions are minimal or if order effects are unlikely to affect the results.

recruiting participants for factorial designs

• Number needed depends on whether are tested between or within-subjects

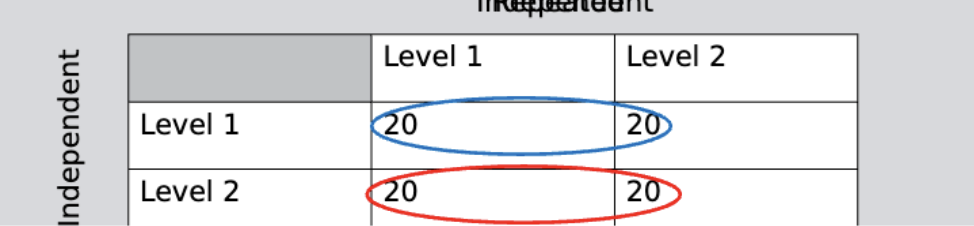
• For a 2x2 design with 20 subjects in each cell

  • 2x2 independent groups factorial

  • 20/cell x 4 cells = 80 subjects needed

• 2x2 mixed factorial

  • 20/cell, same 20 in two cells, different 20 in two other cells = 40 subjects needed

analyzing factorial design

Factorial ANOVA - F score for each main effect and interaction

Independent, dependent, and mixed ANOVA

Post-hoc testing for interactions: simple effects analysis

Factorial ANOVAs and simple effects analyses

Identify a PxE factorial and understand what is meant when such a design produces main effects and interactions

P factor represents a characteristic of the participants (e.g., age, gender, experience) and the E factor represents an environmental variable (e.g., a treatment, condition, or setting).

P (Person factor): Age Group (two levels: Young Adults, Older Adults)

E (Environment factor): Teaching Method (two levels: Lecture-based, Interactive Learning)

Main effects describe the independent impact of the Person or Environment factors.

Interaction effects indicate that the effect of one factor depends on the level of the other factor, showing how the combined influence of the two factors can produce unique outcomes.

Distinguish a mixed PxE factorial from simple PxE factorial designs

Simple PxE factorial designs can either manipulate both factors as between-subjects or both as within-subjects.

Mixed PxE factorial designs manipulate the Person factor as a between-subjects factor and the Environment factor as a within-subjects factor.

simple between subject design

Number of participants = Levels of P×Levels of E×Participants per cell

simple within subject design

Number of participants=Participants per condition(same participants for all conditions)

mixed PxE design

Number of participants=Levels of P×Participants per cell (P)