AP Pre-Calculus Need-To-Know

a²-b²

(a+b)(a-b)

a²+b²

No factor, is prime

a²+2ab+b²

(a+b)²

a²-2ab+b²

(a-b)^2

a³+b³

(a+b)(a²-2ab+b²)

a³-b³

(a-b)(a^2 + ab + b^2)

Function is increasing if

if a < b, then f(a) < f(b)

Function is decreasing if

if a < b, then f(a) > f(b)

Concave Up

Rate of Change is Increasing

Concave Down

Rate of Change is decreasing

Average rate of Change on [a, b]

Slope Formula

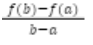
Degree in Standard Form

Highest Exponent

Degree in Factored Form

Sum of exponents

Local Min

1. Polynomial changes from decreasing to increasing

2. At a left endpoint where the polynomial is increasing

3. At a right endpoint where the polynomial is decreasing

Local Max

1. Polynomials changes from increasing to decreasing

2. At a left endpoint where polynomial is decreasing

3. At a right endpoint where polynomial is increasing

Absolute Max

largest y-value

Absolute Min

Smallest y-value

Point of Inflection

when concavity changes signs

End Behavior: Even Degree have

the same end behavior

End Behavior: Odd Degree have

opposite end behavior

Odd-Degree Roots

“cut” through the x-axis

Even-Degree Roots

“bounces” on the x-axis

Even function

f(-x) = f(x)

Odd Function

f(-x) = -f(x)

Positive Right End Behavoir

lim x → infinity f(x) = Infinity

Negative Right End Behavior

lim x → infinity f(x) = -Infinity

Positive Left End Behavior

lim x → - infinity f(x) = infinity

Negative Left End Behavior

lim x → - infinity f(x) = - infinity

Horizontal Asymptote at y = b if

lim x → infinity f(x) = b

lim x → - infinity f(x) = b

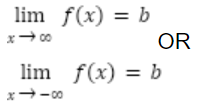
Vertical Asymptote at x = a if

lim x → a^+- f(x) = +- infinity

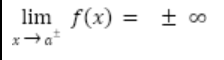
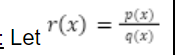
Let r(x) = p(x) / q(x)

When is there a zero

p(x) = 0
q(x) ≠ 0

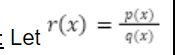
Let r(x) = p(x) / q(x)

When is there a Hole

p(x) = 0
q(x) = 0

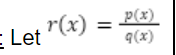
Let r(x) = p(x) / q(x)

When is there a Slant Asymptote

p(x) is 1 degree higher than q(x)

Pascal’s Triangle
Row # ____

Put Numbers for that row (note, first row is degree 0)

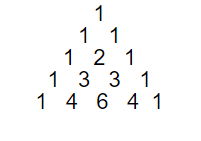
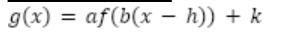
What is a

vertical dilation by a factor of |a|

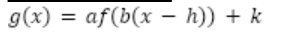
What is b

horizontal dilation by a factor of |1/b|

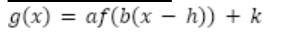
What is h

horizontal translation by h units (left or right)

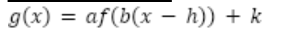
What is k

vertical translation by k units (up or down)

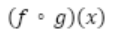
(f * g)(x) =

f(g(x))

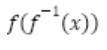
Inverse: f(f^-1(x)) =

x

Arithmetic Sequence equation

a_n = a₀ + dn
or
a_n = a_k + d(n-k)

Geometric Sequence equation

g_n = g₀(r)ⁿ
or
g_n = g_k(r)^{(n - k)}

lim x → infinity b^x =

infinity

lim x → - infinity b^x =

0

lim x → infinity (1/b)^x =

0

lim x → - infinity (1/b)^x =

infinity

b^m * b^n

b^m+n

(b^n)^m

b^m*n

b^-n (Simplified)

1/b^n

b^(1/k) = (simplify)

^k Sqrt B

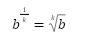
lim x → 0^+ logb (x) =

-infinity

lim x → infinity logb (x) =

infinity

Exponential Growth: y = (in terms of b)

b^x

Decay: y = (in terms of b)

(1/b)^x

Change of base: logb (x) =

loga (x) / loga (b)

logb (xy) = (Expanded Form)

logb (x) + logb(y)

logb (x/y) = (expanded version)

logb (x) - logb(y)

logb (x)^n = (expanded form)

n * logb (x)

b^x = (in terms of c^log something)

c^(logc(b) * x)

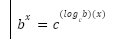
Linear Model for the semi-log plot: (using base of n, and variables b & a)

y = logn(b) * x + logn(a)

sin(θ) =

y/r

cos(θ) =

x/r

a sin(b(θ + c)) + d

midline: y = d
amplitude: |a|
period: 2pi/b
Frequency: b/2pi

a cos(b(θ +c)) + d

midline: y = d
amplitude: |a|
period: 2pi/b
Frequency: b/2pi

sin(θ) = cos(

θ - pi/2

cos(θ) = sin(

theta + pi/2

a tan(b(θ + c)) + d

Period: pi/b
Frequency: b/pi

y = sin^-1(x) Domain and Range

[-1, 1] and [-pi/2, pi/2]

y = cos^-1(x) Domain and Range

[-1, 1] and [0, pi]

y = tan^-1(x) Domain and Range

(-infinity, infinity) and (-pi/2, pi/2)

csc(x)

1/sin(x)

sec(x)

1/cos(x)

cot(x)

1/tan(x)

cos(x) / sin(x)

sin² + cos² =

1

1 + tan² =

sec^2

1 + cot² =

csc^2

sin(A + B)

sin(A)cos(B) + cos(A)sin(B)

sin(A - B)

sin(A)cos(B) - cos(A)sin(B)

cos(A + B)

cos(A)cos(B) - sin(A)sin(B)

cos(A - B)

cos(A)cos(B) + sin(A)sin(B)

sin(2x) =

2sin(x)cos(x)

cos(2x) =

2cos^2(x) - 1

1 - 2sin^2(x)

cos^2(x) - sin^2(x)

Polar x =

rcos(θ)

Polar y =

rsin(theta)

(Polar) x² + y² =

r²

The distance between r and the origin is increasing if

r is positive and increasing OR
r is negative and decreasing

The distance between r and the origin is decreasing if

r is positive and decreasing OR
r is negative and increasing

(Parametric) f(t) =

(x(t), y(t))

min and max of x(t)

horizontal extrema

min and max of y(t)

vertical extrema

t-value when y(t) = 0

x-intercept

t-value when x(t) = 0

y-interceptx

x(t) is decreasing

particle is moving left

x(t) is increasing

particle is moving right

y(t) is decreasing

particle is moving down

y(t) is increasing

particle is moving up

Parametric slope formula for x

(x(t2) - (x(t1)) / (t2 - t1)

(delta x / delta t)

Parametric slope formula for y

(y(t2) - y(t1)) / (t2 - t1)

(delta y / delta t)

Parametric average rate of change =

(delta y / delta t) / (delta x / delta t)

(delta y / delta x)

Ellipse Standard Form

(x-h)² /a²+ (y-k)² /b²= 1