Machine Learning - Test 1

f: X → Y

Where X is the __

• Domain (math)

• Parameter Type (CS)

• Input Type (engineering)

• Key Type (map ADT)

Supervised vs Unsupervised

Supervised we provide input and output while unsupervised only provides input

Data

the information that the model uses to learn patterns and make predictions

f: X → Y

Where Y is the __

• Codomain (math)

• Return Type (cs)

• Output Type (engineering)

• Value Type (map ADT)

Model

The function/program/tool we want to make

Observations/Data Points

The values of a domain of a model

Targets

Values of a codomain of a model

Datasets

Collection of observations collated with targets that once trained can predict new targets when given new

Dimensionality

number of features/attributes of data

Regression

• predicting a continuous #

• Target type is real #’s

• Y = R

Classification

• Y is a finite set

• Target values are labels/classes/categories/tags

Binary Classification

• Only 2 outcomes

• |Y| = 2

• {T,F} , { 1, 0}, {1, -1}

Density estimation

• Target type is [0,1]

• (every value in between 0 and 1)

Model Family

• General form for a class of models

• we try to predict the family to extract something

Model Family example

Linear family would be y = C₀ + C₁x

Parameters (weights/coefficients)

constants used to specify a model in a model family

Parameters example

In model family : y = C₀ + C₁x

C₀ = 5, C₁ = 2 are the parameters

Model example

In model family : y = C₀ + C₁x

y = 5 + 1.75x

Hyperparameters

variables to specify options in a training alg

Training/learning/fitting

Finding parameters to specify a model

Error/Loss Function

• Function chosen to evaluate the model

• lower values = better

Training Set

Portion of data used for training vs testing

Generalization

How well does the model do on data it wasn’t trained on

Overfitting

Model is strict to the training data

A data point in the training set or test set

observation

An input value to the model

Observation

An output value of the model

Target

A “correct answer” to a data point in the training set or test set

Target

A R^D vector

Observation

When the function we're looking for is R^D->{-1, 1}.

Binary Classification

When the function we're looking for is R^D -> R.

Regression

When the function we're looking for is R^D -> Y for some finite set Y.

Classification

When the function we're looking for is R^D -> [0, 1]

Density Estimate

When we want to model a real-valued function.

Regression

When we want to model a probability distribution.

Density estimate

When we want to associate each observation with one of a finite set of labels or categories.

Classification

Variable

contains all values that measure the same attribute across units

Observation

contains all values measured on the same unit (row)

Attribute

A column/instance variable

Feature

value in a column, value of an instance variable

Value

element in the table, measurement, datum, feature

Tidy data

• each var forms a column

• each observation forms a row

• each type of observational units forms a table

Feature Selection

The process of transforming the dataset by keeping only the most informative features

Curse of dimensionality

The phenomenon of the difficulty of training accurate models increasing with the dimensionality of the data

N

# of observations

D

# of attributes (dimensionality)

General - X

data set as NxD matrix

General - y

N length vector of target values

General - n

used as an index into the data set, for example X_n and ⃗y_n

General - i and j

used as indices into features, for example ⃗x_i where ⃗x = X_n

What is the idea behind K nearest neighbors?

With classification, its most likely items from the same class are next to one another → when classifying a new item look at the classes of its k nearest neighbors to determine

KNN algorithm

• compute all distances between new data point and X

• sort by the distances calculated

• take the closest k distances

  • use array bag to tally their classes

• Return class w/ highest tally

KNN - Cost

Depends on size of D:

Distance computations - O(ND)

Sort distances - O(NlgN)

total : O(ND+NlgN) → O(NlgN)

What are the hyperparameters of KNN?

• The number of neighbors

• The distance metric

KNN - when k = 1

• The model perfectly memorizes the data.

• Highly sensitive to noise (one wrong neighbor ruins the classification).

• Very low bias, high variance → Overfitting.

KNN - when k = N

• Every query is classified based on the majority class in the entire dataset.

• Ignores local structure → Underfitting.

Why is KNN non-parametric

It does not assume a fixed form (parameters) for the decision boundary. It memorizes training data and bases predictions on local neighborhoods.

Metric or Distance Function

Any function d between two vectors where:

1. d(x,y) = d(y,x)

2. d(x,z) <= d(x,y) + d(y,z)

3. d(x,y) = 0 iff x=y

What are Norms?

• they measure vector magnitude (size)

• compute the distance between two points

Euclidian Distance

• L₂ Norm

• for general continuous distance

• sqaure root sum of square values

Manhattan/City-block Distance

• L₁ norm

• For general continuous data

• Sum of absolute values

Norm

a mathematical function that measures the size or magnitude of a vector in a given space

KNN properties

• it’s instance based

• lazy, most work is put into classification

• it’s non-parametric, it has no parameters

R or C: Attribute

Column

R or C: Covariate

Column

R or C: Data Point

Row

R or C: Sample

Row

R or C: Feature

Column

R or C: Observation

Row

R or C: Variable

Column

Main problem of Curse of Dimensionality

greater the dimensionality → sparser the data is within the vector space

Regression general form

Given data X (N observations in D dimensions) and N target values as ⃗y, find a function for predicting the values of new data points

Cost

var, function, formula that we want to minimize in an optimization problem

Error

difference between the computed value and the correct value

Loss

• measures how well the model performs

• interprets error

Risk

how well a model performs on all possible data

• difficult since we don’t have all possible data

• expected val of loss function applied to arbitrary data

Empirical Risk Minimization (ERM)

General strategy of finding model that minimizes loss on the training data

linear regression model family

y(x) = θ₀ + θ₁x

How can we make lin reg model family into lin algebra form?

Refer to the params as vectors:

• θ^→=[θ₀, θ₁]

• x^→=[1, x]

and multiply : θ^→ * x^→

What is linear about linear regression?

• output is weighted sum of inputs

• no multiplication between features

• forms a straight line or hyperplane

Simple Linear Regression - Loss Function

SSE - Sum of Squared Errors

(this is for a single input x)

• θ is the slope and intercept

• subtract the estimated y value from the actual

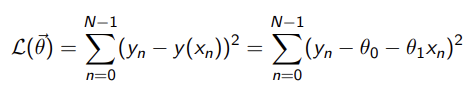
Multiple Linear Regression

• this models multiple input features

• θ_n determines how much impact it’s corresponding x_n has

• θ₀ is the intercept still and we extend the x vector by one to match the length of the θ vector

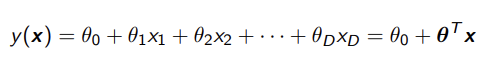
Multiple Linear Regression - Loss Function

Same as linear regression but on larger scale, subtracting predicted from the actual y and doing matrix multiplication to get the square

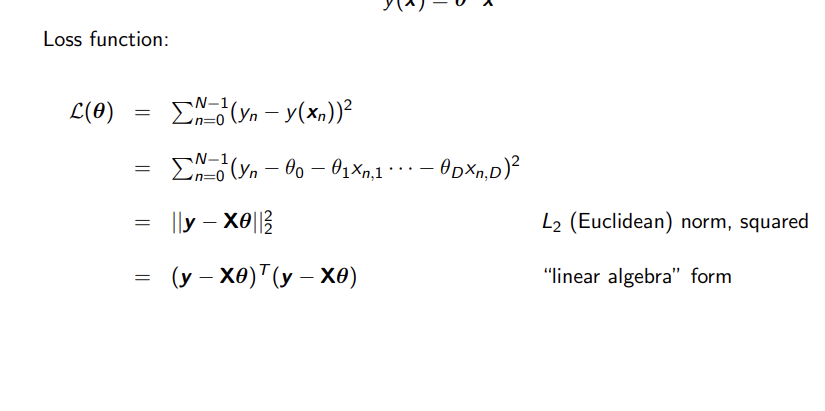
What is regularization?

This adds an extra term to a normal loss function which penalizes large values of the model parameters/weights (θ) making prediction more general → preventing overfitting

Ridge Regularization

• essentially linear regression with an L2 penalty on the weights

• α controls strength of penalization → larger α → smaller coefficients

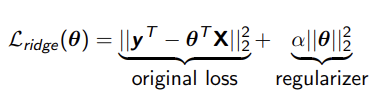
Lasso Regularization

• Uses the L1 penalty instead * α to determine strength

• uses Feature Selection and eliminates any features that are irrelevant

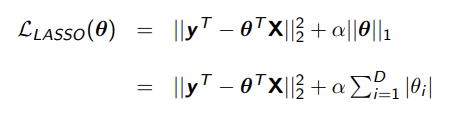
Closed Form Solution

Provides a direct formula for how to get the optimal parameters that minimizes loss without using things like gradient descent

Which versions of linear regression have a closed form solution?

• linear regression

• Ridge regression

• XX Lasso (absolute val - non differentiable) XX

What is Gradient Descent

Minimizes a function, typically loss by adjusting the parameters to the steepest descent and can be used on functions that don’t have a closed form solution.

Gradient Descent General Outline

1. Initialize parameters to random vector

2. Compute loss with those parameters

3. compute gradient → tells direction of steepest descent

4. update to new parameters

5. repeat until change is negligible or max iterations

Basis Functions

transform x inputs into a more flexible representation → polynomial regression to be captured in a linear space

Premise of adapting linear regression for classification

when we apply the sigmoid logistic function to lin reg → output between 0 and 1 → interpret it as a probability of being in a certain class

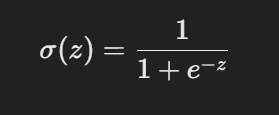
Logistic Function (sigmoid function)

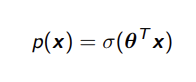
Model family for logistic regression

Use of logistic function

• maps real val input to range (0,1) for classification purposes

• smooth version of the step function

Logistic Function useful properties

It has a nice derivative to work with

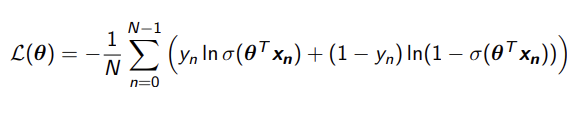
• mean log loss

• loss function for logistic regression

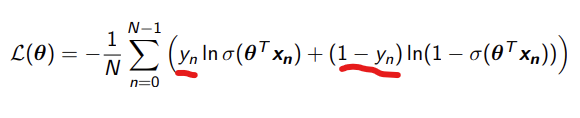
these will either be 0 or 1 and will determine which error to use

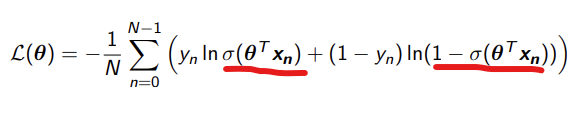
This is how far off the estimate is

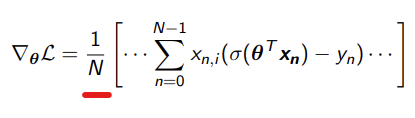
We divide by N because we are getting the mean