Limits

limit

the intended height of a function

~ DO NOT HAVE TO EQUAL THE VALUE OF THE F(x)!~ (I.e a limit could equal a hole/open circle)

Do limits always exist ?

no

one side limits

• always exist

• approaching the same value both either from the left( -) or right (+)

• would cause the limit for just that value to not exist(DNE)

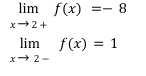
limits that do not exist (DNE)

• when an x values has both one sided limits causing the limits of x- & x+ to not equal each other

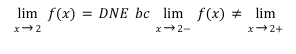
interpreting limits examples

“as the limit approaches x-value, f(x) = ?”

f(x) can be an open circle value

• for one-sided limits, look at the function at the absolute end of side your approaching from

can a limit be undefined?

NO (only DNE)

can a value be undefined?

YES

Steps for solving algebraic limits

1.) direct substitution

2.) factor

3.) conjugate method

• if you one doesn’t solve the limit, try the next

• ALWAYS END WITH SUBSTITUTION

When to use what: factoring

• for problems when both the denominator AND numerator equal zero after the initial substitution

• after substitution the polynomial is factorable

When to use the conjugate method

• If the function after substitution equals 0/0

• How to use: multiply denom/numer by the same value but opposite symbols(it would remove a sqrt)

  *When multiplying a sqrt by a sqrt the sqrt symbol is removed (if the value in the radicals are the same then, when multiplying the radical will be removed -obviously tho…)

What do you always end an evaluation with?

direct substitution!!!

How to use to solve an absolute value limit?

would always be written as |a| /a so the two value will cancel out to equal 1

~| a | will always be positive!!! ~

-if there is a value before the | |, distribute for final answer

1.) direct substitution

2.) breaking function into one sided limits

3) lim from the left= negative value; lim form the right = positive value

How to solve rational functions

~if function = x/0 →-/+ infinity ~

1.) direct substitution

2.) separate limits into one sided lims

• for limits from the left, all values will be less than that it’s approaching so the limit = - infinity

• for limits from the right, all value will be greater than that it’s approaching so the limit = + infinity

Do rational function limits(non-one-sided) not exist?

Technically yes and no, as they would be both positive and/or negative infinity

solving piecewise function limits

1) break down parts of the function into one-sided limits

2) direct substitution

3.) see if one sided limits equal each other to determine If the limit exists

** distractors for these problems will be piecewise functions with no variables

How to solve infinite solutions pt.1

• power of num = power of denom→ratio of leading coefficients

• power of denom > power of num → 0( case bc since the denom power is >, the function will always equal a number close to 0 making it negligible and simplified as 0)

• power of num > power of denom →+ /- infinity

  ~all based on leading powers~

How to solve infinite solutions pt2

num> denom: explore the function as -/ +or +/+ or -/-, then after evaluating the signs, evaluate it with the sign of the infinity being approached

num=denom: divide coefficient of num by the coefficient of denom

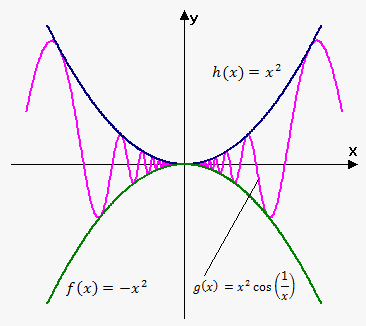
Squeeze theorem

• always explored as a compound inequality

  1.) Evaluate the limits for the exterior(left/right) functions

  ~limits for both will always be the same ~

  2.)if both exterior limits are the same the the value of those limits = value of the limit of the squeezed/sandwiched function

Finding the limit using a table

1.) look for value very close to that being approached, in the table

2.) Label or determine which would be the left or right limits

3.)If values are very close together, make an educated “guess” or approximation of what the value of the limit would be

~ if there is much of a difference between the left and right limit, then the limit does not exist~