stats final exam

Any straight line can be defined by

Slope (b1) and intercept (b0)

Sum squared accounts for

Improvement in prediction model

Residuals account for

Error in prediction

F value accounts for

Overall fit of the model

Standard error accounts for

The extent that values vary across populations

R2 accounts

Overall variance in model (whtever decimal point x100)

Multiple regression formula

Yi = (b0 + b1 of X1 + b2 of x2) + error

Eg: immobility= b0 + b1TMS + b2Taser + error

What formula is this

Multiple regression

Regression plane

Tells us about positive and negative real

Regression assumptions

Linearity, homoscedasticty, independent errors, normality, and outliers

How to check linearity and homoscedasticity assumption

Scatter plot

Homoscedasticity wasn’t met (heteroscedasity)

Homoscedasticity Is met

Independent error assumption

Makes sure data set is reflective of what is meant to be looked at (should come from independent sources)

How to check normality assumption

Histogram or qq plot

How to check outliers assumption

Cooks distance (if output is more than 1, we should inspect potential influential cases)

Multicollineraity

Arises in multiple regress when predictors are highly correlated (.8=concern)

Residual of 0 means what

Model correctly predicts the outcome value

Did not meet normality assumption

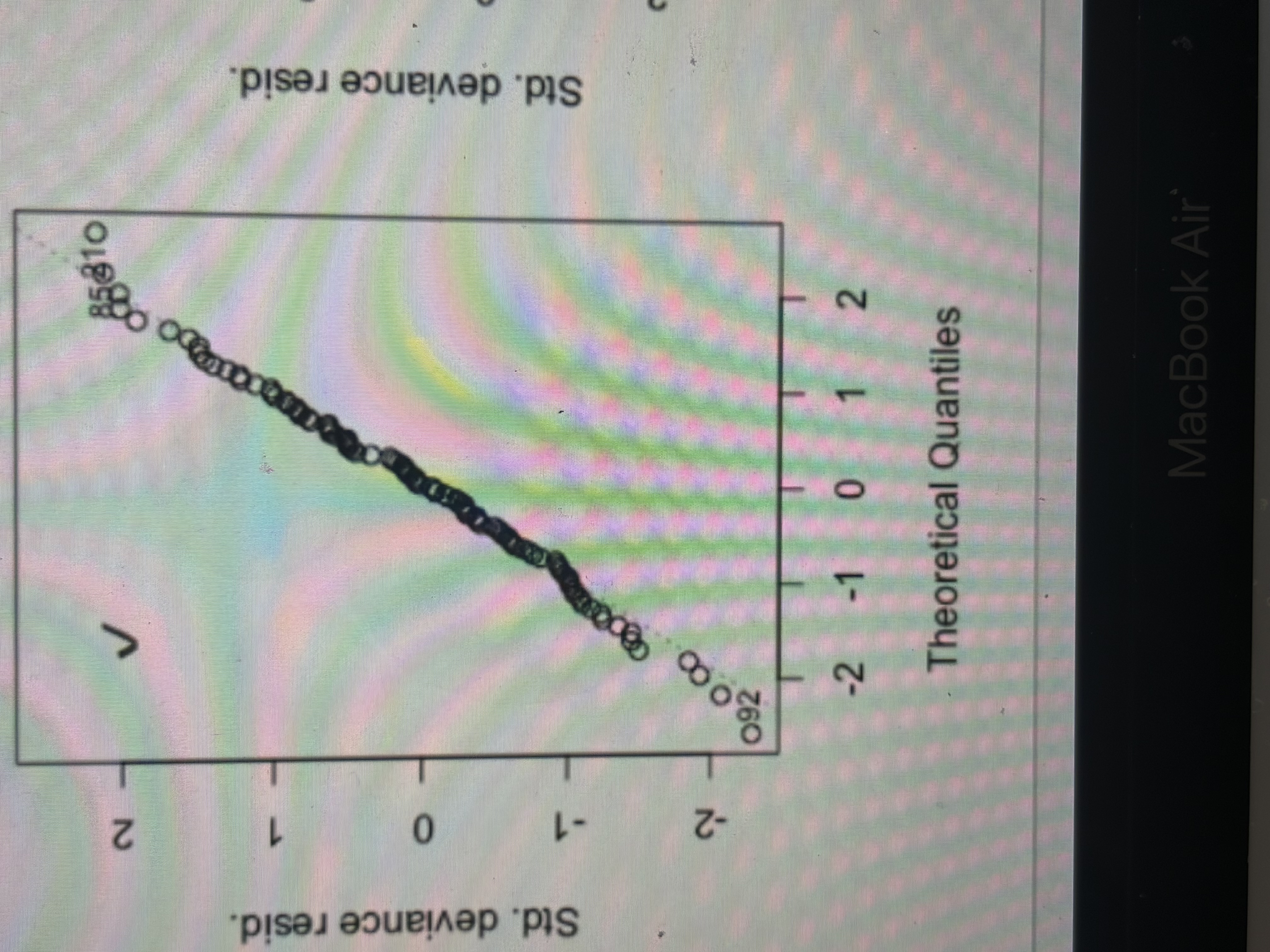
Did meet m normality assumption

Multicollinearity

Good because non are over .8

Hierarchical regression

Predictors are selected based on previous work and you decide the order of the predictors

Forced entry

Dump all predictors you have or are interested into the model

Stepwise

Decisions about the order in which predictors are entered in the model based on mathematical decisions

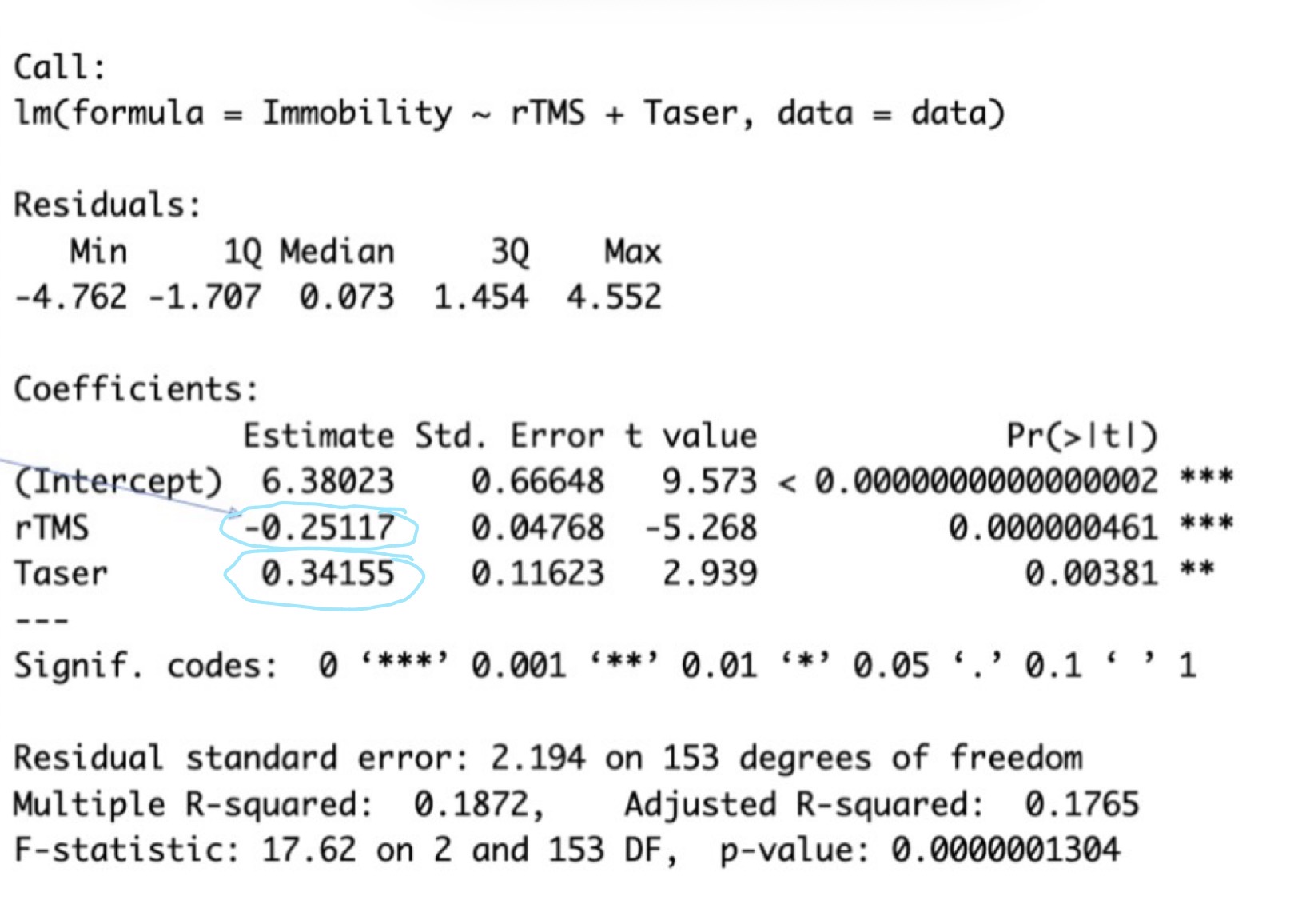
What do the circled numbers tell us

As rTMS frequency decreases by 1 unit zombies will be immobilized for an extra 0.251 seconds

As voltage increases by 1 unit zombies will be immobilized for an extra 0.342 seconds

What does the standard error tell us

To what extent values vary across different samples

what does R² tell us

18.7 of the variance in immobility time can be accounted for for by taser and rTMS

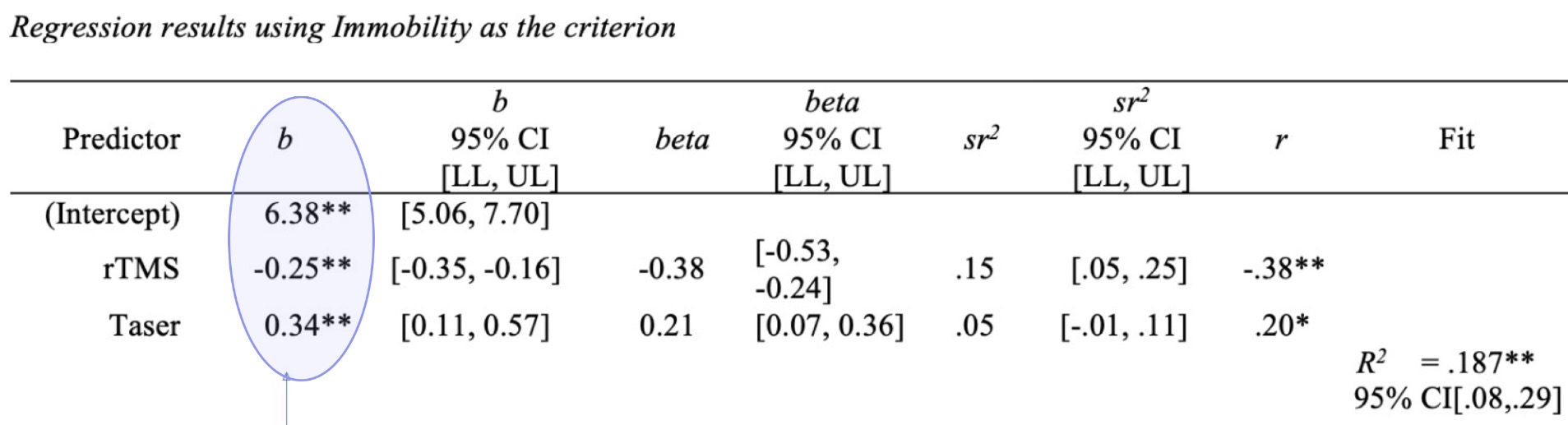
What is b

Unstandardized beta (we can’t compare units)

Beta

Standardized betas: in SD units so we can compare

Interpret beta

As rTMS decreases by 1 SD, zombies will be immobilized for an extra 0.38 if a standard deviation, controlling for the effect of taser (vise versa for taser)

Based on this info rTMS effect in zombie immobility is a little stronger than the taser voltage effect

T-tests

Looks at group mean difference

Independent samples t-test

Compares 2 means from 2 different groups (between subjects)

Eg: Did the right side of the class do better than the left side in the midterm

Pairs samples t-test

Compares mean from the same people just different conditions (within subjects)

Eg: does our midterm grades differ from our final exam marks

What type of t-test is this

Independent because 1 participant is only in 1 condition

What type of t-test is this

Paired samples because each participant is in multiple conditions

The simplest form of an experiment

One that has 1 IV manipulated in 2 ways and 1 DV

Eg: does listening to music help with exam performance (IV= music and no music DV=grades)

When can independent t-test be used

When there’s 2 IV levels and 1 DV

Null hypothesis

There’s no effect (t-test null = no difference between means)

Alternative hypothesis

There’s a real effect (t-test alternative null = 2 means come from different distributions)

P<.05

Reject null (there’s a difference)

P>.05

Fail to reject the null (there’s no difference)

Test statistic equation

Variance explained by the model (effect)

Variance not explained by model (error)

*want the top part to be bigger*

Assumptions of independent t-test

Scores are independent, normality, homogeneity of variance

How to we calculate homogeneity of variance

Levens test (want this to be non significant)

What does it mean if CI don’t overlap

1. Both CI contain the mean but come from different populations

2. Both samples come from same population but one (or none) contain the mean

What does it mean if you CI contains 0 (eg. -0.314, 2.378)

Cannot reject the null (don’t have a significant effect)

What does it mean if CI doesn’t contain 0 (eg. 0.782, 7.218)

Can reject the null

Effect size

Tells you the magnitude of your effect and is not dependent on sample size

Cohens D equation

D= estimated mean difference

Estimated standard deviation

D= 0.20

Small effect

D= 0.50

Medium effect

D= 0.80

Large effect

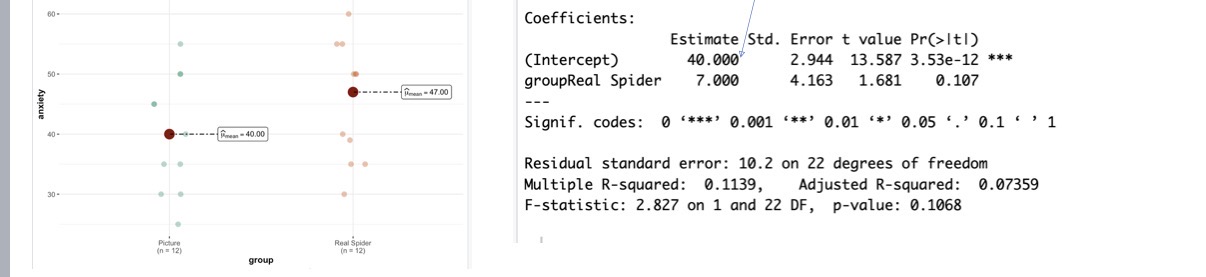
What does value for 40 and 7 mean

40= the intercept

7= the increase for every 1 unit

Pros of within subject research design

Exact same people are in both groups

Desire removed extra noise

Cons of within subject designs

Time may have an effect on scores

Order effects

Practice effects

We can fix this using counterbalancing

ANOVA (analysis of variance)

Tests mean differences between 2+ (several) groups —> must have a categorical IV and a continuous DV

Goal of ANOVA

To see if there’s a significant mean difference between groups

Types of ANOVAS

1. Between subjects

2. Within subjects

3. One way

4. Factorial

5. Repeated measure

Between subjects ANOVA (one way)

compares means form 2+ separate groups

Within subjects ANOVA (RM)

Comparing 2+ means within the same people

One way ANOVA

Examining only 1 factor

Eg. Mean vocabulary scores across 3 age groups (3,5,7). IV is age and this has 3 levels

Factorial ANOVA (2-way, 3-way, 4-way, etc.)

Examining more than 1 factor (IV)

Eg. Mean vocabulary scores across age groups and gender (can be within or between subjects or mixed)

How does ANOVA calculate variance

Calculates total variance ten separates it into between-treatments and within treatments variances

Do we want a large f value

Yes (#of explained variance)

Type of variance

Between treatments

Type of variance

Within treatments

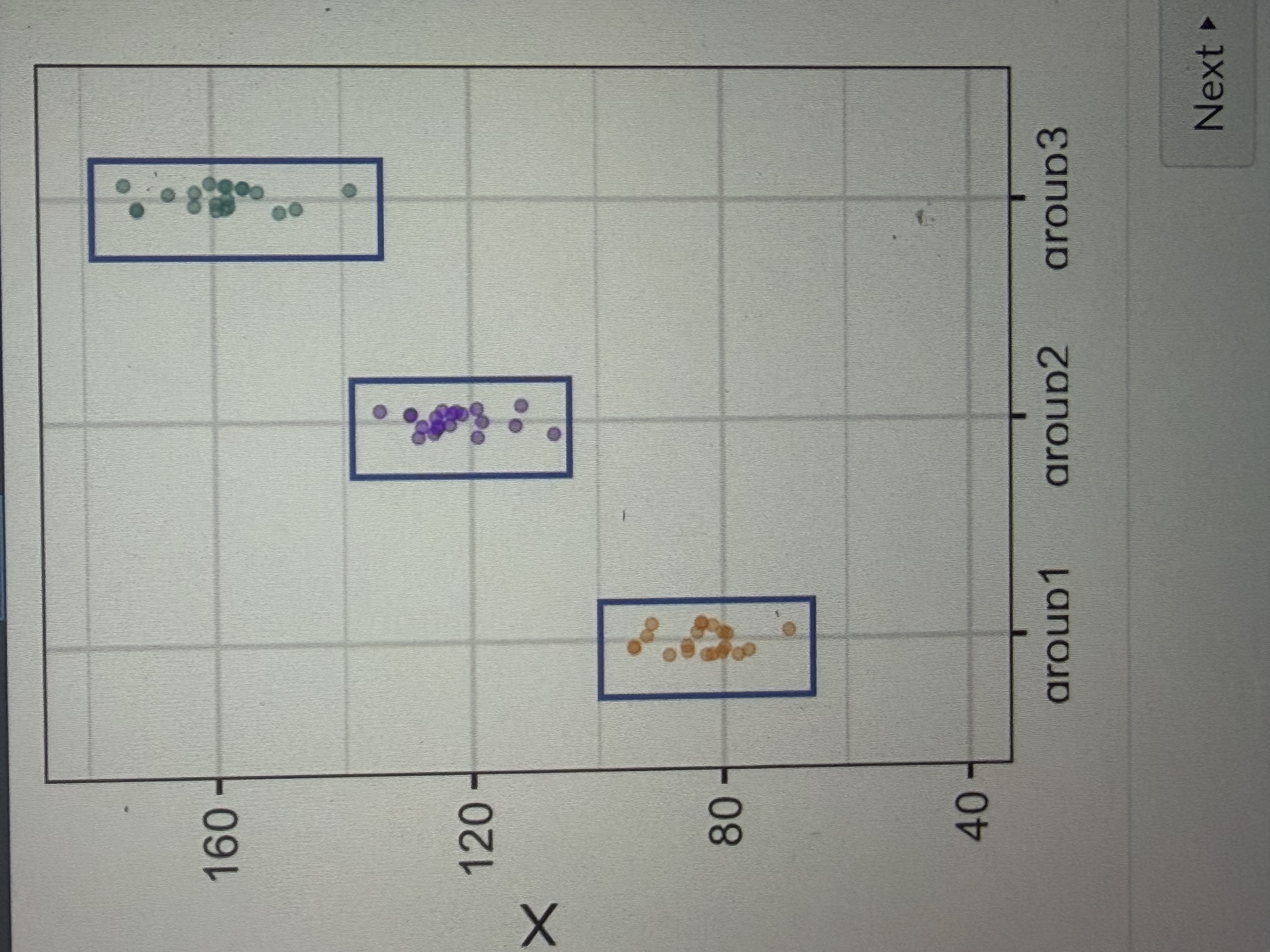
Would this F value be small to large

Large because the variance is small

Is this F value small or large

Small because it’s spread out which indicates a larger variance

ANOVA assumptions

1. Observations in each sample must be independent

2. Normality (qq plot or histogram)

3. Homogeneity (levens test—> sig= bad)

What do we do if our levens test is sig in our ANOVA

Welsh test

Effect size ANOVA

ETA squared (n²) = effect size for between subject ANOVA

n² equation for ANOVA (effect size)

N² = ss between

ss total

N²= 0.01 ANOVA

Small effect

N²= 0.06 ANOVA

Medium effect

N²= 0.14 ANOVA and how to interpret it

Large effect; 14% of the variance is explained by between subject treatment

Between groups df equation

K (number of groups) - 1

Within subjects df equation

N (number of people) - K (number of groups)

When should you use post hoc

If u rejected null hypothesis

Have 3 or more treatments (k>3)

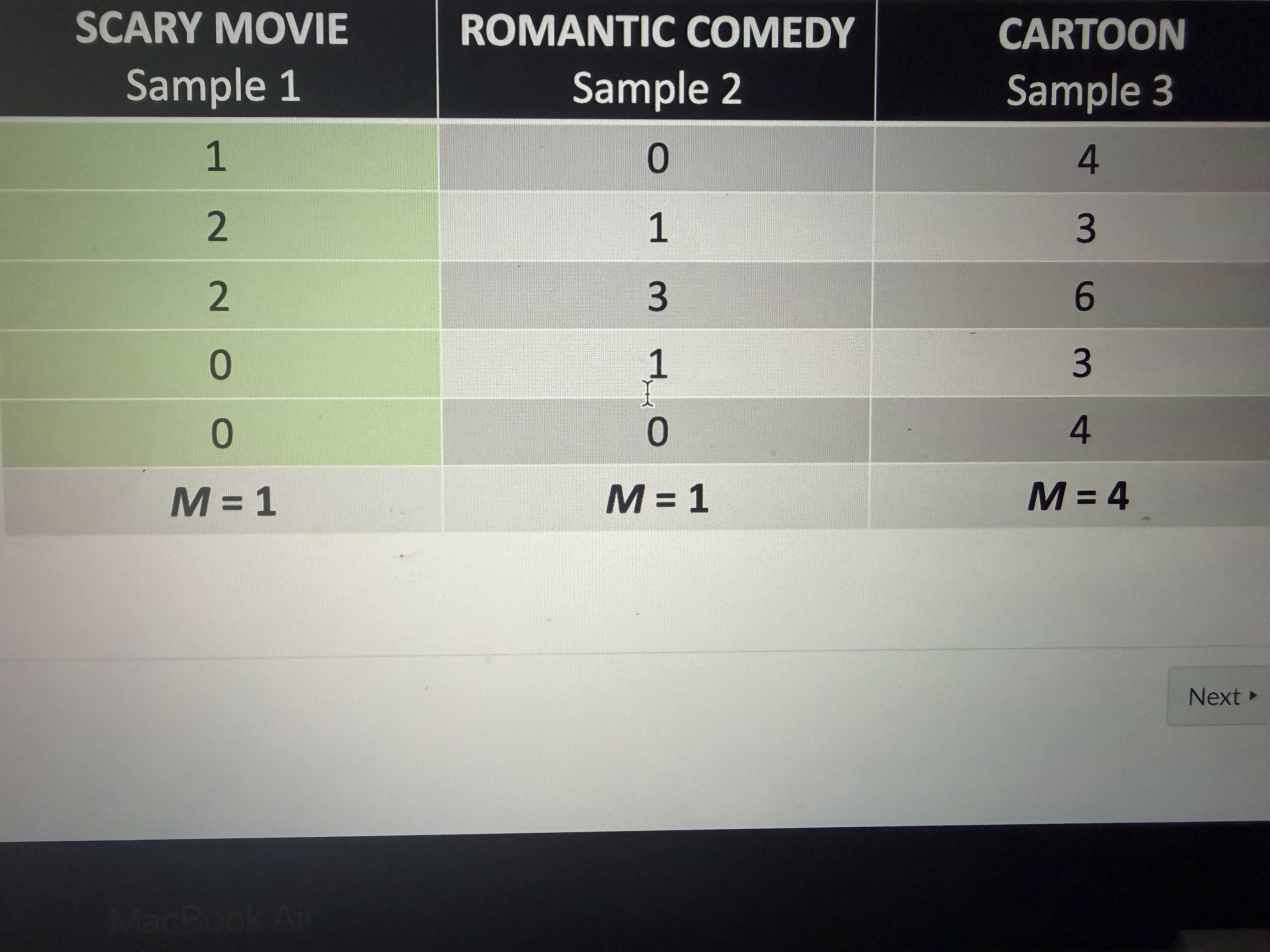
SSt- total variance in data

Difference between the observed data and grand mean

SSm accounts for

Variance explained by the model (improvement due to the model)

SSr accounts for

Unexplained variance (error)

SSt accounts for

Total variance in the data

SSr- unexplained variance

Difference between the observed data and group means (ignore black line in image) (error)

SSm- variance explained by the model

Difference between grand mean and group means (improvement due to model)

MSm equation

SSm

DFm

MSr equation

SSr

DFr

Benefits of factorial ANOVA

Helped and some more complex questions and takes into account the interactions of factors

Does aggression different across gender and conditions (violent versus nonviolent video games)? Wht type of design is this

Factorial ANOVA

What’s the effect of gender

8, and 4

What’s the effect of the condition

5, and 7

Is there an interaction between a&b

No, because the effective condition was similar for both genders

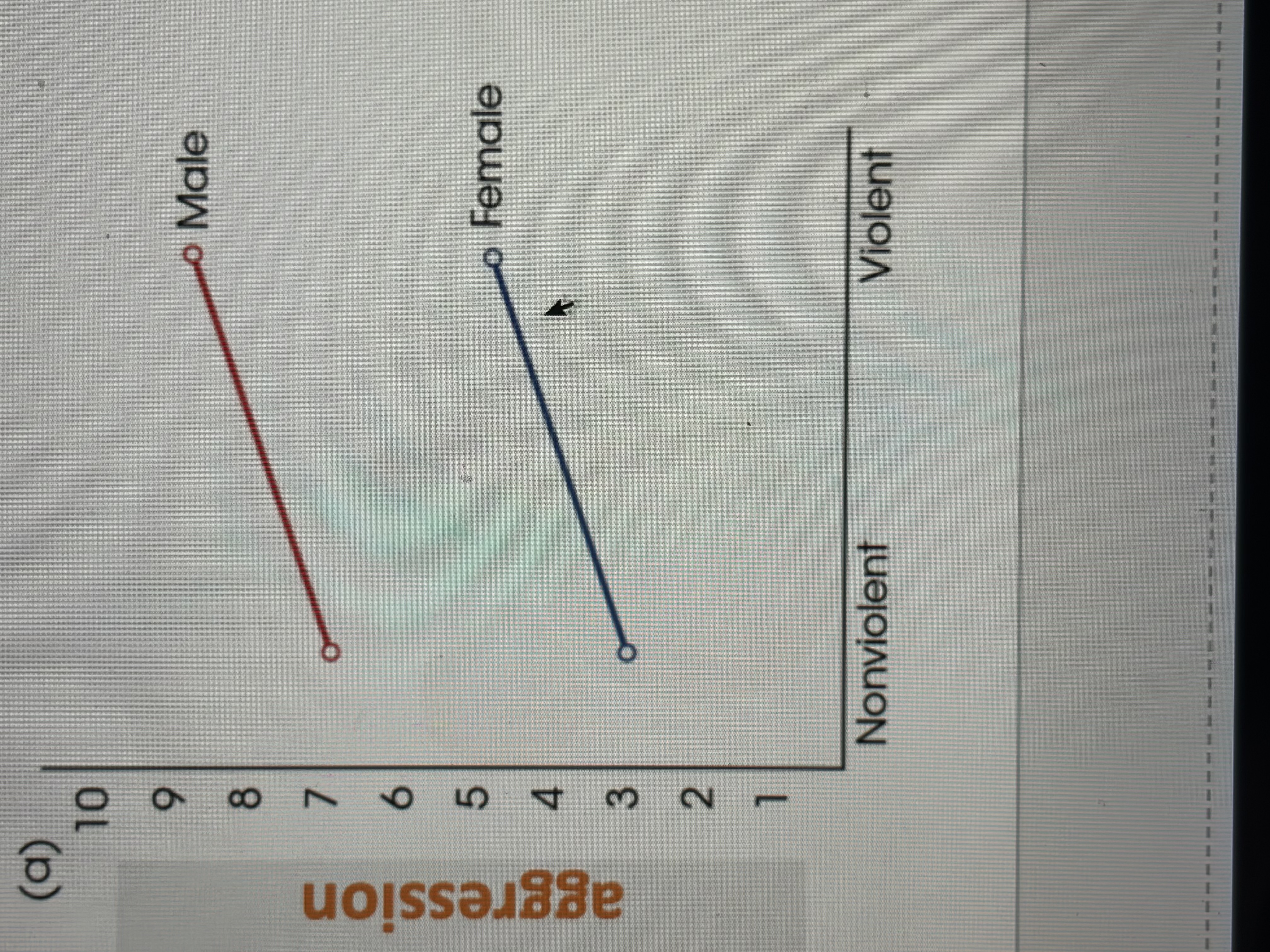
Is there an interaction between a and b

Yes, condition had an impact on males aggression, but didn’t seem to affect females aggression at all

Parallel lines regarding interaction

Indicates no interaction

Different slopes regarding interaction

Indicates an interaction

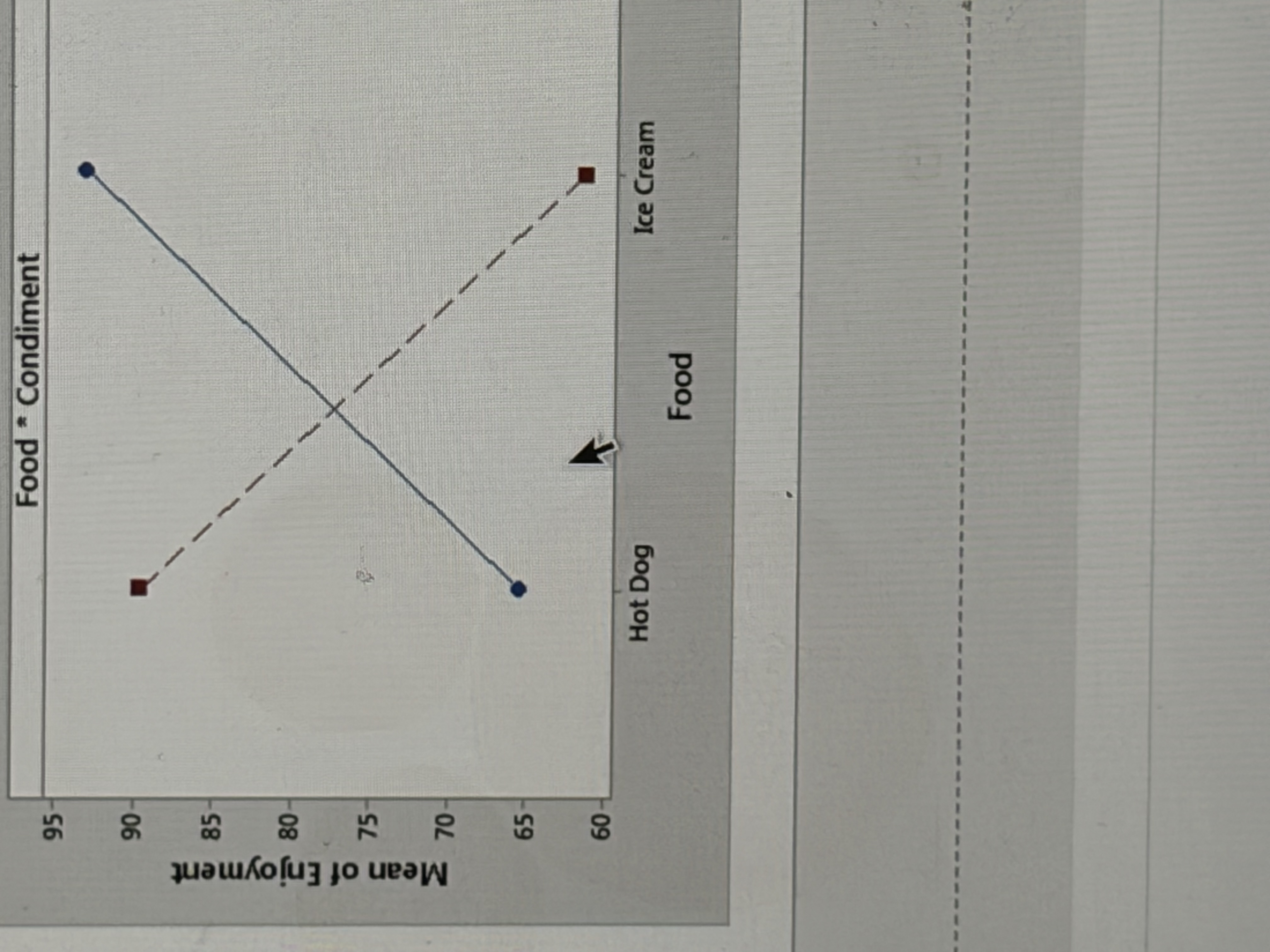
Opposite patterns regarding interaction

Indicates interaction

Can we assume an interaction based off graphs without actual testing?

No

SSa

Variance explained by variable A

SSb

Variance explained by variable B

SSaxb

Variance explained by interaction of A and B