AP Statistics Unit 6

Just some useful notes for the AP Stats. Fomula Sheet: https://apcentral.collegeboard.org/media/pdf/statistics-formula-sheet-and-tables-2020.pdf.

(6.1) How do we determine if the evidence for a claim is convincing?

• Consider the two explanations for the evidence (random chance, real effect).

• Estimate the probability of getting evidence as strong or stronger than the observed evidence by chance alone.

• If you can eliminate random chance as a plausible explanation for the evidence, the evidence for the claim is convincing.

(6.2) How do we verify the conditions for calculating a confidence interval for a population proportion

1. The data is calculated using a random sample from the population

2. When sampling without replacement, the sample size is less than or equal to 10% of the population size.

3. Both np̂ ≥ 10 and n(1 - p̂) ≥ 10

(6.2) How do we determine the margin of error when estimating a population proportion?

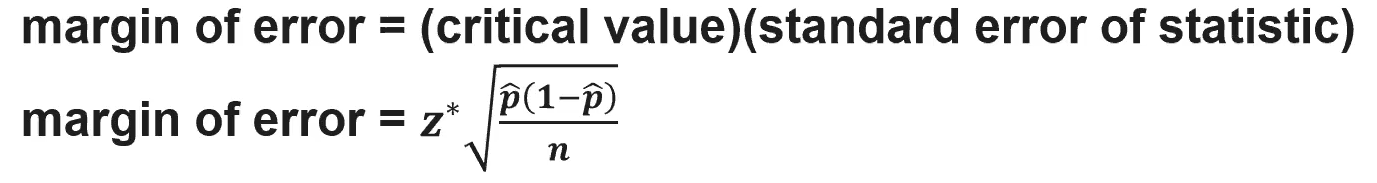
(6.2) How do we calculate a confidence interval for a population proportion?

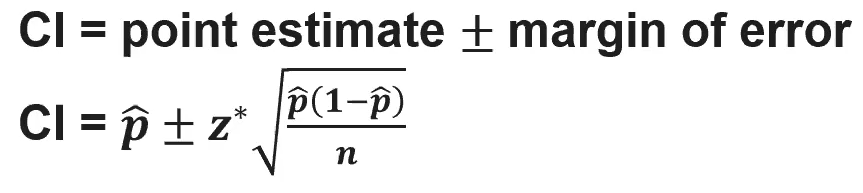
(6.2) How do we determine the minimum sample size that will achieve a given margin of error?

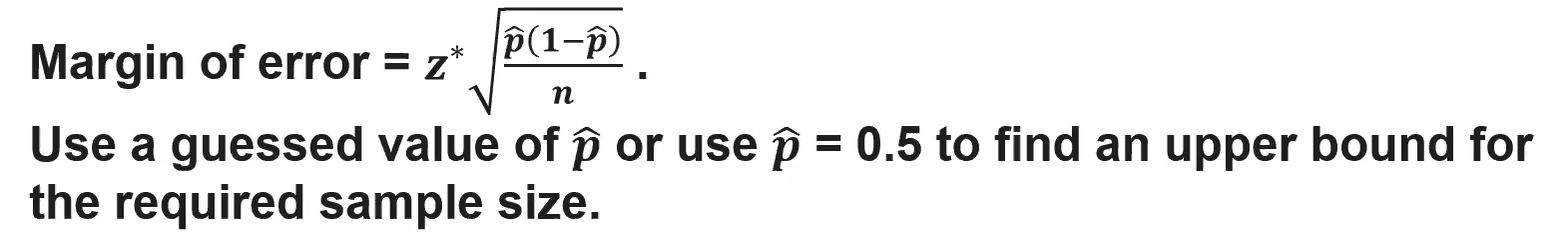
(6.3) How do we interpret a confidence interval for a population proportion?

“We are C% confident that the interval from ___ to ___ captures the [population parameter].”

(6.3) How do we interpret a confidence level for a confidence interval for a population proportion?

In repeated sampling with the same sample size, approximately C% of C% confidence intervals will capture the population proportion.

(6.3) How do the sample size and confidence level affect the margin of error for a confidence interval for a population proportion?

Assuming everything else stays the same:

• Increasing the sample size will decrease the margin of error.

• Increasing the confidence level will increase the margin of error.

(6.4) Null & Alternative Hypotheses

(6.4) How do verify the conditions for performing significance test for a population proportion

1. The data is collected using a random sample from the population.

2. When sampling without replacement, the sample size is less than 10% of the population size

3. Both np₀ ≥ 10 and n(1 - p₀) ≥ 10, where p₀ is the proportion specified by the null hypothesis.

(6.1/2/3/4) When dealing with hypotheses…

P₀ is used instead of p̂ since we are assuming the null hypothesis (H₀) is true until convinced otherwise

(6.5) How to calculate a standardized test statistic using the AP Statistics Formula Sheet

(6.5) How do we calculate an appropriate test statistic in a test for a population proportion?

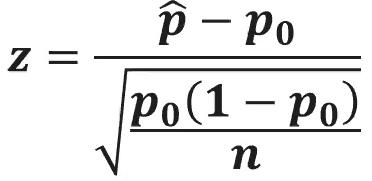
(6.5) How do we calculate a p-value in a test for a population proportion?

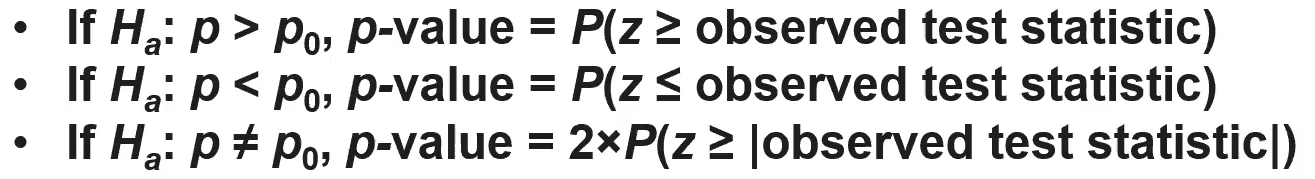
(6.5) How do we interpret the p-value in a test for a population proportion?

(6.6) How do we make a conclusion in a test for a population proportion.

(6.6) How do we perform a significance test for a population proportion?

(6.6) What do you do if there is no stated significance level?

(6.7) How do we identify and interpret Type I and Type II errors?

(6.7) How do we calculate the probabilities of Type I and Type II errors?

(6.7) What factors affect the power of a test and probabilities of errors in significance testing?

(6.8) How do we verify the conditions for calculating a confidence interval for a difference in proportions?

1. Two random samples or two groups from a randomized experiment

2. When sampling without replacement, sample sizes are less than or equal to 10% of the population sizes. (Doesn't apply to experiments.)

3. The counts of successes and failures are all at least 10.

   n₁p̂₁ ≥ 10, n₁(1 − p̂₁) ≥ 10, n₂p̂₂ ≥ 10, and n₂(1 − p̂₂) ≥ 10

(6.8) How do we calculate a confidence interval for a difference in proportions?

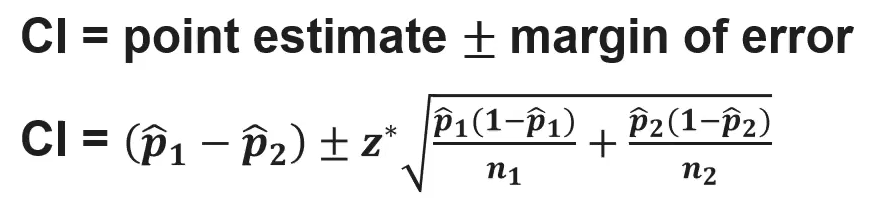
(6.8) How do we interpret a confidence interval for a difference in proportions?

“We are C% confident that interval from __ to __ captures the [value to be estimated].”

Note: if the value from __ to __ falls into 0, the proportions would be the same and their difference would be the same.

(6.9) How do we construct and interpret a confidence interval for a difference in proportions?

Be sure to:

• Define the difference in proportions you are trying to estimate.

• Indicate the direction of the difference.

• Define any subscripts you use.

• Identify the procedure you are using.

• Verify that the conditions for the procedure are met.

• Calculate the confidence interval.

• Interpret the interval in context.

(6.10) Significance Tests for a difference in proportions

(6.9) How do we verify the conditions for performing a significance test for a difference in proportions?

Note: p̂_C = combined proportion of successes / combined number of observations

(6.10) How to calculate a test statistic and p-value for a significance test of a difference in proportions.

(6.11) How do we interpret and state a conclusion for a significance test for a difference in proportions?

(6.11) How do we perform a complete significance test for a difference in proportions?