section 4.3: Linear Independence and Bases

A set of vectors is linearly independent if c₁v₁ + … + c_nv_n = 0 and has only the trivial solution?

c₁ = … = c_n = 0

proof: Show that a set of vectors is linearly dependent if and only if there is some vector v_j that can be written as a linear combination of the other v_i , i does not equal j

That is, for some 𝑗 we have 𝑐𝑗≠0. Solving for 𝒗𝑗 thus gives use the linear combination 𝒗𝑗=−𝑐1𝑐𝑗𝒗1−⋯−𝑐𝑝𝑐𝑗𝒗𝑝.

Now suppose 𝒗𝑗 can be written as a linear combination of the other 𝒗𝒊, 𝑖≠𝑗. Then we can write 𝒗𝑗=𝑐1𝒗1+⋯+𝑐𝑝𝒗𝑝

Moving all the terms to the same side we have 𝟎=𝑐1𝒗1+⋯+𝑐𝑝𝒗𝑝−𝒗𝑗

is a solution to 𝑐1𝒗1+⋯+𝑐𝑝𝒗𝑝=𝟎 with a nontrivial solution.

Basis

a set of vectors that are linearly independent and spans the space. B spans V, V= SpanB

if A is in R^n and A has n pivots then the matrix is..

invertible

A matrix A being invertible means the matrix has _____ columns

linearly independent

How many pivot columns does this matrix B have?

3

Find a basis for the column space of the following matrix A

Solution: Since 𝐴~𝐵=1 4 0 2 0

0 0 1-1 0

0 0 0 0 1

0 0 0 0 0

What is the row space of A, Row A

the span of row vectors of A

What is the row space of this matrix A

the first three rows

Null space qualifications

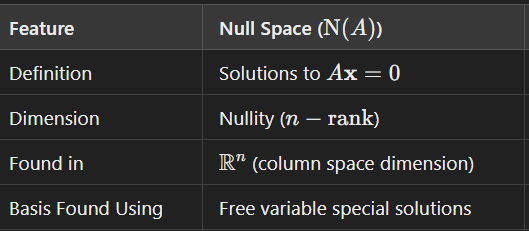
Row space qualifications

rank of nullity theorem

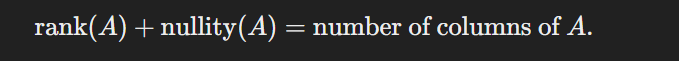
for a set of vectors to span R³, the set must have __ pivots

3

A set of vectors has two pivots, do these vectors span R²? Do they span R³?

they DO span R², they do NOT span R³

A set of vectors has 4 pivots, do they span R³? What about R^4?

the vectors do NOT span R³, they have more than 3 pivots meaning they span a higher dimension.

The set DOES span R^4 as there are 4 pivot columns

If a set contains 4 vectors but only 3 pivots, how many columns are linearly independent?

3

If a set contains four vectors but has only 3 pivots, do the vectors span R³ or R^4? Why?

They DO span R³. While there are four vectors, having only 3 pivots means that there are only 3 vectors that are linearly independent, meaning that the set spans R³.

If there were 4 pivots, the set would span R^4.

T/F: A single vector by itself is linearly dependent

F

T/F: A linearly independent set in a subspace H is a basis for H

F

T/F: if H= span {b1,…,bn}, then {b1….bn) is a basis for H

T

(T/F) If a finite set S of nonzero vectors spans a vector space V, then some subset of S is a basis for V.

T

(T/F) The columns of an invertible n×n matrix form a basis for ℝn.

T

(T/F) A basis is a linearly independent set that is as large as possible.

T

(T/F) A basis is a spanning set that is as large as possible.

F

(T/F) The standard method for producing a spanning set for Nul A, sometimes fails to produce a basis for Nul A.

F

T/F) In some cases, the linear dependence relations among the columns of a matrix can be affected by certain elementary row operations on the matrix.

T

(T/F) If B is an echelon form of a matrix A, then the pivot columns of B form a basis for Col A.

F

(T/F) Row operations preserve the linear dependence relations among the rows of A.

T

(T/F) If A and B are row equivalent, then their row spaces are the same.

T

polynomials of degree at most 2 can have have polynomials x up to x^?

x²

polynomials of degree at least 3 can have polynomials x up to x^?

x³

Given T:V→W as in Exercise 47, and given a subspace Z of W, let U be the set of all x in V such that T(x) is in Z. Show that U is a subspace of V.