Introductory Research wk1-2

UniSA BEHL2019

What is statistical thinking?

A way of understanding a complex world by describing it in relatively simple terms.

These simple terms summarise and capture essential aspects of the

structure or function (or both) of the data

We can use statistics to

describe, decide and predict.

Important statistical concepts

learning from data, aggregation, uncertainty, sampling, causality and statistics

qualitative data

Descriptive representations of information, e.g. barriers to exercise

qualitative data collection

typically, interviews and focus groups

quantitative data

Numerical representations of information, e.g. average university grade point average

quantitative data collection

typically, observational and experimental studies

binary data

0 v 1 (yes v no), discrete

integer data

whole number, discrete

real number data

decimal component, continuous

a variable (factor) is a

measurable characteristic that must vary (have at least two possible measures)

height and sleep quality are variables

but not gender or school (these are constants)

nominal scale

Each value of the variable represents something different. For example, we might ask people for their country of birth, and then code those as numbers: 1 = “Australia,” 2 = “Austria,” 3 = “Azerbaijan” and so on.

ordinal scale

Each value can be ordered in terms of their magnitude. For example, we might ask a person how good their sleep is, using a 1-7 numeric scale.

interval scale

has all of the features of an ordinal scale, but in addition, the intervals between units on the measurement scale can be treated as equal. The scale can also take on negative values

ratio scale

has all the features of an interval scale, with the difference being that the ratio scale variable has a true zero point. A standard example is physical height

identity

each value of the variable has a unique meaning

magnitude

the values of the variable reflect different magnitudes and have an ordered relationship to one another

equal intervals

units along the scale of measurement are equal to one another. This means, for example, that the difference between 1 and 2would be equal in its magnitude to the difference between 19 and 20

absolute zero

the scale has a true meaningful zero point. For example, for many measurements of physical quantities such as height or weight, this is the complete absence of the thing being measured

type ok

ok

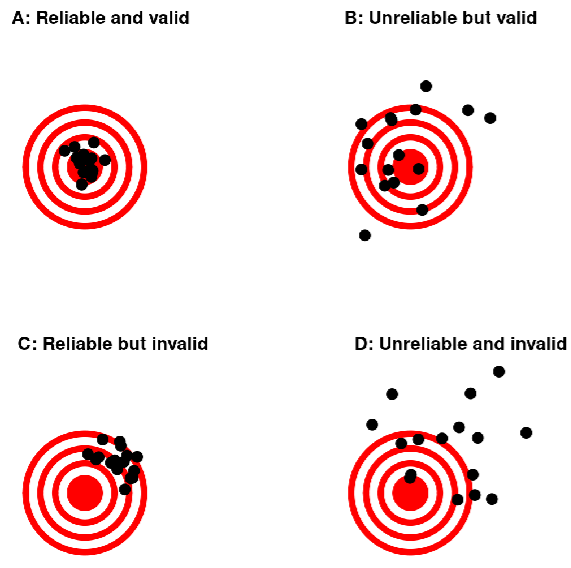
type ok

ok

type ok

ok

cross-sectional designs

capture data at one point in time

longitudinal designs

capture data at multiple points in time

quasi-experimental designs

do not manipulate any variables, participants are subject to non-random assignment

population-based sample

representative of the population. e.g. random sample of Medicare numbers

convenience sample

not representative of the population. e.g. clinic-based or through social media advertisement

stratified sampling

based on pre-defined groups. e.g. equal numbers of 5-9, 10-14 and 15-19-year-olds.

Methods need to be appropriate to address your research aim.

Sampling biases should always be recognised and attenuated where possible.

outcome variable

is being measured in relation to the predictor; usually an exposure (e.g. risk or protective factor)

predictor variable

is a factor of interest and is being measured. Outcomes and predictors are used in observational research

you must ___ key terms

operationalise

you must ____ all key variables/factors

define

difference between research question and aim

they’re the same; one is a question